Avant Après – Désignation des contours de la figure plane avec des

Créations maths du 28 mai 2014 – 6 élèves de CM2 (groupe 2) – Buxerolles Planty (86) Philippe GILG
Avant Après
–Désignation des contours de la figure plane avec des points (lettres en majuscule)
–prolongation possible des segments par des droites / Notion de croisement par un point
(exemple : "les droites d 1 et d 2 sont sécantes en G")
–Mesures des côtés des triangles reconnus sur la figure plane ("quand deux côtés sont de
même longueur ont fait le même nombre de traits") T LAC est rectangle, T BDE est équilatéral,
T DEF est isocèle
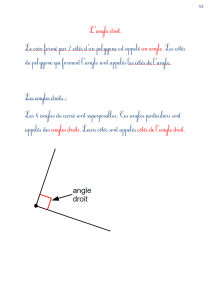
–reconnaissance et révision des angles aigus, obtus et droit grâce à l'utilisation de l'équerre
Avant Après
–reconnaissance des formes planes : quadrilatères (4 côtés) => carré, rectangle, losange,
quelconque ; 5 côtés = pentagone : 6 côtés = hexagone.
–Mesures des côtés des quadrilatères pour les différencier et marquage avec la technique vue
dans la 1ère création (un trait, deux traits, etc ...)
–"- Qu'est ce qui a la forme d'un hexagone ? - la France !"
–"- Le carré est à la fois un losange et un rectangle ! - ah bon ?! - ben oui, ça dépend si les
côtés sont de même longueur et si il n'y a que des angles droits."
–" - Et quand un carré est sur une pointe ? - c'est un losange !... - ah bon ? - mais non c'est
encore un carré !" :)

Créations maths du 28 mai 2014 – 6 élèves de CM2 (groupe 2) – Buxerolles Planty (86) Philippe GILG
Avant Après Avant Après
–pas d'axe de symétrie sur la figure de gauche ..... un axe de symétrie sur celle de droite
–"Comment transformer la figure plane de droite pour qu'il y ait un autre axe de symétrie ? -
il faut modifier la pointe qui est en bas ! - Ok vas-y. - Vous êtes d'accord ? - Oui, il y a la
même distance par rapport à l'axe de symétrie horizontal !"
–repérage des angles aigus (en vert), obtus (en bleu) et droits (en rouge) sur la figure de
gauche. Elle a dix côtés. "- Comment ça s'appelle une figure plane à 10 côtés ? - un dixone
ou un dizone ?? - On pourrait vérifier en cherchant sur un ordi ?" Après vérification, on
appelle cela un décagone.
–"Et combien de côtés sur celle de droite ? - 12 ! - Et comment ça s'appelle ? - Un
douzone !?" Après recherche, on vérifie qu'il s'agit d'un dodécagone
Avant Après
–repérage des angles : deux aigus identiques en bas ("sur la base") et un obtus en haut (" à la
pointe") ==> "C'est un triangle isocèle !" :)
–100 + 100 = 200
–"- Pourquoi 100 ? - parce que ..." "- On pourrait mesurer les angles ! - ça se mesure ?!" (le
maître nous a dit que ça se mesurait avec un rapporteur. On essaiera plus tard parce qu'on
n'a pas cet outil en classe en CM2).
–"- Et si on reliait les sommets à la croix ?" " - On est en 3D !" " - On obtient une pyramide !"
–discussion sur les solides (en 3D). Les élèves connaissent le pavé droit et le cube.
–Validation en manipulant une poche avec d'autres solides comme la sphère, le cône, les
pavés. Travail sur le nombre et la forme des faces (carrés, rectangles, trapèze,
parallélogramme, ...), rapport avec le nombre de sommets. Patrons de solide sur feuille, ...