puissance electrique et energie electrique

PUISSANCE ELECTRIQUE ET ENERGIE
ELECTRIQUE
I/ Puissance électrique
Un résistor est caractérisé par la valeur R de sa résistance et aussi la puissance
nominale qu’elle peut dissiper.
La puissance électrique reçue par un dipôle est donnée par : P= U.I avec U=R.I
d’après la loi d’Ohm, ainsi P=U.I = R.I2
avec P en Watt , U en Volt , I en Ampère , R en Ω
Cette puissance est dissipée sous forme de chaleur. C’est l’effet Joule.
Si on demande à une résistance de dissiper une puissance trop importante, elle peut :
- Soit être détruite,
- Soit changer fortement de valeur sans modification de son aspect extérieur.
Dans la pratique, il convient de ne pas dépasser la puissance nominale.
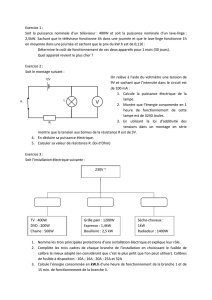
Exemple 1 : Peut-on sans danger appliquer une tension de 6V à une résistance marquée
(18Ω ; 1W) ?
Réponse : U= 6V ; calculons l’intensité de courant qui peut traverser la résistance :
D’après la loi d’Ohm : U=R.I , d’où I= U/R ; I = 6V/18Ω= 0,33A
La puissance dissipée et reçue est donc : P = U.I = 6V. 6V/18Ω =2Watt
P= 2Watt>1Watt = puissance nominale ⇒ on ne doit pas appliquer 6V à ce
composant.
Exemple 2 : La puissance absorbée par un appareil dépend de l’effort qui est exercé sur
cet appareil.
Une perceuse à courant continu, pour modélisme, est alimentée sous une tension de
18V. Mesurons l’intensité I du courant qui la traverse :
a)Lorsque la perceuse tourne à vide : I= 0,25A
b) Lorsqu’ on perce un morceau de bois, l’intensité augmente et peut atteindre 1,1A
suivant l’épaisseur. Calculons la puissance absorbée par la perceuse dans les deux cas :
- Si I=0,25A ;P= U.I =18*0,25 =4,5Watt
- Si I=1,1A ; P= U.I = 18*1,1= 19,8Watt
On remarque que la puissance absorbée dépend de l’effort qui est exercé sur la mèche.

Exemple 3 : Puissance consommée par un appareil soumis à différentes tensions ;
indications sur la lampe ( 6V – 3W) .
Tension U en Volt
Intensité de courant I en
Ampère
Puissance dissipée P=U.I en
Watt
1,7
0,25
0,425
2,6
0,32
0,832
4,0
0,41
1,640
5,8
0,50
2,900
6,1
0,51
3,111
7,6
0,58
4,408
9,2
0,64
5,888
Circuit :
Interprétation :
- La puissance et l’intensité augmentent lorsque la tension croît ;
- La lampe brille normalement pour une tension voisine de la tension nominale, la
puissance dissipée est alors proche de la puissance nominale ;
- Pour une tension inférieure, elle brille moins, la puissance consommée est alors
inférieure à la puissance nominale ;
- Pour une tension supérieure, elle brille d’un éclat très vif, elle consomme une
puissance supérieure à sa puissance nominale. La lampe est alors rapidement
détériorée, on dit qu’elle est grillée.
Conclusion :
Les valeurs nominales sont des valeurs utilisées pour le bon fonctionnement de l’appareil.
II/ Energie électrique
1-De quoi dépend l’énergie électrique ?
L’énergie électrique consommée par un appareil dépend de sa durée de
fonctionnement et de sa puissance.

Pour économiser l’énergie électrique, il est conseillé de :
- Limiter la durée de fonctionnement des appareils.
Exemple : Une lampe fonctionnant pendant 2heures consomme deux fois plus d’énergie
électrique qu’en 1heure.
L’énergie consommée est proportionnelle au temps.
- Limiter la puissance des appareils
Exemple : La puissance des premiers téléviseurs était de 600W environ, actuellement,
elle est de 100W.L’énergie consommée est divisée par 6 à durée de fonctionnement
égale.
L’énergie consommée est proportionnelle à la puissance
Conclusion :
Nous admettrons que l’énergie électrique E consommée par un appareil est égale au
produit de sa puissance électrique P par la durée t de passage du courant dans
l’appareil.
E= P.t or P= U.I => E = U.I.t
U en Volt ; I en Ampère ; t en seconde et E en J
Exemple d’application : Calculons l’énergie consommée par un four de cuisinière
électrique, de puissance 3.5 kW, fonctionnant pendant 1h 30min.
Réponse :
L’énergie électrique E consommée par la four : E= P.t
E = 3,5kW =3500W ; t =1h30min = 5400s => E= 3500*5400= 18900000J
=18900kJ
L’unité Joule est très petite, c’est pourquoi on utilise parfois d’autres unités : le Wh et
le kWh.
1Wh =1Watt.1h = 1Watt. 3600s =3600J et 1kWh = 10-3 Wh
D’où E = 5250Wh =5,25kWh
2-Energie électrique consommée dans une installation
Le compteur électrique mesure l’énergie électrique totale consommée dans une
installation. Le montant de la facture d’électricité dépend de la consommation
enregistrée par le compteur.
Le compteur électrique est traversé par la totalité du courant qui alimente l’installation ;
il donne directement la consommation en kilowatt-heures (kWh).
Application :

Le locataire d’un studio n’ayant pas de compteur individuel veut évaluer sa
consommation moyenne mensuelle. Pour cela, il relève la puissance des appareils et leur
durée d’utilisation moyenne pour un jour. Calculer l’énergie consommée en moyenne
pour un mois de 30jours, ainsi que le prix de l’électricité en un mois de 30jours si 1kWh
coûte 360ariary.
Appareils
Puissances des appareils
Durée d’utilisation
Lampes
360W
6h
Téléviseur
100W
3h 30min
Réfrigérateur
300W
480min
Radiateur
2kW
5h 30min
Réponses :
Energie : E = P.t
L’énergie consommée en une journée par chaque appareil est :
- Lampes : 360*6 =2160Wh
- Téléviseur : 100*3.5 =350Wh
- Réfrigérateur : 300*8 =2400Wh
- Radiateur : 2000*5.5 = 11000Wh
Consommation journalière totale : 15910Wh
Consommation mensuelle moyenne : 15910 * 30 = 477300Wh =477,3kWh
Coût de l’électricité en un mois de 30jours : 477,3*360 =171,828 ariary
Conclusion :
L’énergie consommée dans une installation est égale à la somme des énergies
consommées par chaque appareil .Elle est mesurée par le compteur électrique en kWh.