ultrasons - effet Doppler

Ultrasons - Effet Doppler
Principe du radar
1. Mesure de la vitesse du son
1.1. Mesure de longueur d'onde.
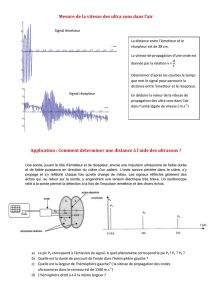
Les fréquences sonores audibles sont celles de l'intervalle de 20 Hz à 20 kHz. L'émetteur et le
récepteur dont on dispose fonctionnent sur une fréquence voisine de 40 kHz, donc dans le
domaine des ultrasons.
• L’émetteur et le récepteur sont identiques. Ils fonctionnement
indifféremment selon un mode ou l’autre (fonctionnement
réversible !).
• Placer émetteur et récepteur à quelques centimètres en face
l'un de l'autre. Alimenter l'émetteur par le générateur BF
(Figure 1)
• Observer à l'oscilloscope le signal reçu par le récepteur en
faisant varier la fréquence du GBF.
G BF
Oscillo
Emetteur Récepteur
Figure 1
• Choisir la fréquence du générateur BF de façon à avoir une amplitude maximale au niveau
du récepteur. Mesurer cette fréquence. L’émetteur et le récepteur fonctionnent alors au
voisinage immédiat de leur fréquence de résonance mécanique. L’amplitude de l’onde
ultrasonore émise est ainsi maximale (de même que l’amplitude de l’onde électrique
engendrée par le récepteur).
• Comparer les signaux émis et reçu quand on éloigne ou qu'on rapproche le récepteur de
l'émetteur. Expliquer en particulier les variations de la phase relative des deux signaux.
• En déduire la longueur d'onde à la fréquence considérée, puis la célérité cs du son dans l'air.
• Le déphasage du à la célérité finie de propagation du signal électrique dans les fils doit-il
être pris en compte dans le calcul ?
On montre que pour un gaz parfait de masse molaire M, à la température T,
cRT
M
s=γ où
γ = cp / cv.
• Avec γ ≈ 1,4 pour l'air et M = 29 g.mol-1, calculer cs à la température de la pièce ( ≈ 20°C).
Conclusion ?
Pour expliquer les variations de l’amplitude reçue lorsque l’on fait varier la distance émetteur -
récepteur, on suppose, dans un premier temps, que l’onde sonore se propage sans atténuation
selon l’axe constitué par le système émetteur - récepteur et que ceux-ci se comportent comme
des murs parfaitement rigides. Sachant qu’une onde sonore correspondant à une onde de
déformation longitudinale ξ(x,t) du milieu de propagation (ici l’atmosphère de la pièce) :
• Montrer que l’onde émise par l’émetteur se réfléchie en totalité sur le récepteur et que cette
onde de retour se réfléchie également en totalité sur l’émetteur (cf. problème de la corde).

Ultrasons - 2 -
• En déduire que, pour une pulsation donnée (imposée par l’émetteur), l’amplitude de l’onde
sonore passe par un maximum à chaque fois que la distance L séparant l’émetteur du
récepteur peut s’écrire L = n L0, n ∈ N*. Quel est le lien entre L0 et la longueur d’onde λ de
l’onde sonore ?
• Reprendre l’observation des signaux obtenus en faisant varier la distance L. Interpréter les
variations d’amplitude observées au niveau du récepteur.
• Quels éléments du modèle précédent faut-il “ retoucher ” pour pouvoir interpréter les écarts
par rapport à la prévision théorique précédente ?
1.2. Utilisation d'une cible réfléchissante mobile
On peut recevoir dans le récepteur l'onde réfléchie par
une cible mobile. Si l'on fait varier d de façon
continue, le déphasage ϕ entre le signal émis et le
signal reçu varie lui aussi continûment.
G BF
Oscillo
E
RCible
0 d(t)
Figure 2
• Déterminer le lien entre ϕ et d en supposant que la
cible est un mur rigide (impédance infinie).
• Que se passe-t-il si on fait l’hypothèse d’une cible
non rigide ?
Pour faire varier d, monter la cible
• soit sur le bras mobile de la table traçante ; on engendrera le mouvement de la cible en
commandant le déplacement horizontal (X) à l’aide d’une tension variant de façon affine avec
le temps. Une signal triangulaire de fréquence très basse est bien adaptée (me demander si
nécessaire).
• soit sur le pied spécial mobile sur un banc, dont la vitesse dépend de la tension d'alimentation
( tension continue ≤ 12V prise sur une alimentation stabilisée ).
• Observer qualitativement les variations de ϕ sur l’oscilloscope. Interpréter.
Utilisation d'un comparateur de phase analogique
Pour déterminer plus précisément le déphasage ϕ, on peut, par exemple, fabriquer une tension
proportionnelle à cos(ϕ). C’est l’objet du montage de la Figure 3. e(t) (resp. r(t)) représente le
signal électrique sinusoïdal (pulsation ω) arrivant sur l’émetteur (resp. provenant du récepteur).
Le signal S(t) engendré par le multiplieur est :
e(t)
r (t)
multiplieur Sfiltre
passe-bas VsX k
Figure 3
(
)
(
)()
St ketrt
=
où k est une constante dépendant du circuit utilisé
pour faire la multiplication.
• Décomposer S(t) sous forme d’une somme de
fonctions sinusoïdales (analyse de Fourier).
• Montrer que Vs(t) est bien un signal proportionnel à
(
)
[
]
cos ϕt à condition que la fréquence de
coupure du filtre passe-bas soit bien choisie.
Mise en forme de r(t)

Ultrasons - 3 -
Le signal reçu par le récepteur est d'autant plus faible que la distance est grande. Or, pour que
le montage précédent fonctionne correctement, il est préférable que les tensions e(t) et r(t) aient
à peu près la même amplitude. Pour cela, placer entre le récepteur et le multiplieur un montage
amplificateur non inverseur (mieux adapté qu’un amplificateur inverseur) réalisé avec un
amplificateur opérationnel et deux résistances. Les résistances ne devront pas être inférieures à
1 k Ω .
Utilisation du multiplieur
Le multiplieur PHYTEX utilisé donne en sortie :
S = k (X1-X2)(Y1-Y2) + Z k = 0,1 V-1
On porte donc :
• e(t) en X1 (bien sûr entre X1 et la masse)
• r(t) en Y1
• on court-circuite avec la masse les entrées X2, Y2 et Z.
On obtient alors à la sortie S : s = k. e(t) r(t).
Remarques :
• les entrées X et Y ont une forte impédance d'entrée (10 M Ω )
• les tensions maximales à porter sont + 10 V (sinon le multiplieur sature) pour une
alimentation ± 15 V
• la bande passante est de 1 MHz.
• pour éviter la saturation, on doit brancher en parallèle sur le récepteur une résistance de
≈ 100 Ω ( déjà fait dans le tube support pour les récepteurs montés dans des tubes).
Choix du filtre
Ve
R
CVs
Figure 4
Construire un filtre passe-bas de type “ RC ” de fréquence de coupure de l'ordre de 100 Hz. On
prendra une résistance de l’ordre de 1 à 5 k Ω .. Expliquer le choix de la fréquence de 100 Hz.
Remarque : le signal k.r(t) n'est pas tout à fait sinusoïdal car les transducteurs piézo-électrique
formant l’émetteur et le récepteurs ne sont pas tout à fait linéaires et déforment donc les
signaux. Les harmoniques de r(t), multipliés par e(t), produisent des termes de fréquences
multiples de 40 kHz et sont donc aussi éliminés par le filtre.
Observation de la tension Vs à l'oscilloscope à mémoire.
Puisqu'on doit faire varier la distance d de la cible très lentement, la période de Vs est beaucoup
trop lente pour que Vs soit observée à l'oscilloscope classique. On se sert donc de l'oscilloscope
à mémoire : on utilise le mode ROLL On démarre le mouvement de la cible et on presse RUN
pour enregistrer plusieurs périodes.

Ultrasons - 4 -
Pour déterminer la vitesse du pied mobile sur le banc ou du bras de la table traçante, on
utilisera un chronomètre.
Observation de Vs sur l’ordinateur
On porte Vs sur une entrée de la carte de transfert. Ne pas oublier de relier la masse de la carte
à celle du montage.
• Faire l’acquisition de Vs sur une durée correspondant à environ 2 à 3 périodes ;
• Démarrer la cible et presser F10 pour l'acquisition ;
• Si la courbe est trop "en escaliers", on peut la lisser (Menu TRAITEMENTS/Lissage) ;
• Mesurer la période de Vs ;
Quelque soit la méthode d’acquisition de Vs (oscilloscope à mémoire ou ordinateur), en déduire
la valeur de la célérité des ondes sonores dans la pièce. Comparer à la valeur précédente et à la
valeur théorique. Commenter la précision de la méthode.
2. Effet Doppler.
L'effet Doppler est utilisé, par exemple, dans le domaine de la médecine pour
atteindre la mesure du débit sanguin. Son principe est transposable dans le domaine
des ondes électromagnétiques : radar de détection de vitesse des voitures,
applications militaires, etc.
2.1. Principe de l'effet Doppler
Soit un couple émetteur - récepteur. Le récepteur est placé à l’origine des coordonnées de l’axe
Ox. L’émetteur se déplace à la vitesse V constante sur cet axe. L’émetteur émet un “ bip ”
périodique (période T). Le premier “ bip ” est émis à t0 = 0, le second à t1 = T, le troisième à
t2 = 2T, etc...
• Déterminer l’instant auquel le récepteur reçoit le premier “ bip ”, le second ”bip ”, etc. En
déduire la période T’ du signal perçu par le récepteur. Distinguer en particulier le cas d’un
émetteur et d’un récepteur se rapprochant du cas où ils s’éloignent.
• A quelle vitesse et dans quel sens doit rouler une voiture de pompiers dont la sirène émet les
notes La-Sol pour qu'une oreille absolue qui l'entend passer détecte Si-La ? Dans la gamme
dite "tempérée" (octave divisée en 12 demi-tons égaux) on dit que 2 sons forment un
intervalle de 1 ton si le rapport de leurs fréquences f'/f vaut 2
6.

Ultrasons - 5 -
2.2. Application à la mesure de la vitesse d'une cible.
Contrairement au cas précédent, l'émetteur et le
récepteur sont fixes, mais l'onde se réfléchit sur
une cible mobile à vitesse v.
E
Rd (t)
Cible
v
x
Figure 5
• Montrer que l’onde reçue par le récepteur fixe
est identique à celle émise par un émetteur
mobile dont on donnera la localisation en
fonction de la position de la cible (effet
miroir).
• Exprimer la fréquence f’ perçue par le récepteur en fonction de la fréquence f de l’émetteur et
de la vitesse de la cible.
• Estimer l’écart ∆f = f’ - f en fonction des données expérimentales.
• Combien de chiffres significatifs sont-ils nécessaires sur la mesure de f et de f’ pour faire une
mesure significative de ∆f ? Cette précision est-elle accessible avec le fréquencemètre intégré
dans le générateur BF ?
Principe d'un radar Doppler
On cherche à obtenir une tension
proportionnelle à ∆f et éventuellement à
l'amplifier dans un rapport donné avant de la
mesurer .
e(t)
r (t)
multiplieur filtre
passe-basX k
s
Figure 6
• Montrer que l’on peut mesurer la vitesse
de la cible en utilisant le montage de la
Figure 6 identique à celui déjà utilisé dans
le §1.2.
• Connaissez-vous des applications de cette méthode de mesure de v ?
Remarque : la présence du filtre élimine aussi les échos parasites reçus par le récepteur,
provenant de réflexions sur les obstacles fixes de la pièce, et dont la fréquence est la même que
celle de l’émetteur.
• Observer s(t) à l'oscilloscope à mémoire. Enregistrer plusieurs périodes.
• Mesurer l'écart temporel entre deux maximums à l'aide des curseurs. En déduire la la vitesse
de la cible.
On refera la mesure pour diverses vitesses de cible, dans un sens et dans l'autre, et on
comparera avec les vitesses mesurées directement au chronomètre.
On peut aussi porter comme précédemment Vs sur SYNCHRONIE.