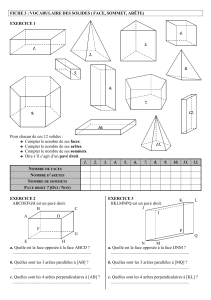
Sous-groupes finis de SO(3)

Sous-groupes finis de SO(3)
Cours d’Algèbre I
MMFAI 2000
1 Groupes des isométries directes de polyèdres réguliers
1.1 Le tétraèdre
Remarque 1.1 Rappelons que le tétraèdre régulier est un polyèdre à 4sommets, 4faces (triangles équi-
latéraux identiques) et 6arêtes de même longueur.
Soit Gle groupe d’isométries directes du tétraèdre T= [A, B, C, D].Gagit sur les sommets (points
extrémaux) de T, et stabilise O, centre de gravité de T.Gest donc un groupe de rotations d’axe passant
par O.
Théorème 1.2 (Ordre) Gest un groupe à 12 éléments.
Preuve :
Soit g∈G.
–1er cas : l’axe ∆de gpasse par un sommet (Apar exemple).
(OA)⊥(CD), donc ginduit une isométrie du plan (BCD)qui laisse invariant le triangle équilatéral
[B, C, D]. C’est donc une rotation plane d’angle 2π
3ou 4π 3. Pour chacun des 4axes, on obtient ainsi
un sous-groupe cyclique d’ordre 3. D’où 8éléments d’ordre 3.
–2ème cas : l’axe coupe une arête.
gest une isométrie, donc l’axe coupe cette arête en son milieu, par exemple I=m[AB]∈∆. Comme
∆passe par O, il passe aussi par J=m[CD]. Cette rotation est donc d’angle π. On obtient donc
un sous-groupe cyclique d’ordre 2pour chaque paire d’arêtes opposées. D’où 3éléments d’ordre 2.
–3ème cas : l’axe coupe une face.
Par exemple, ∆coupe (ABC)en P. Supposons un instant que P A 6=P B. Alors g(A)∈ {C, D}.
Si par exemple g(A) = D, alors g(B) = C. Dans ces conditions g(C)∈ {A, B}. En fait, g(C) = B
car sinon, P A =g(P)g(A) = P D =g−1(P)g−1(D) = P B. On en déduit que l’axe coupe (AD)et
(BC)en leur milieu (et nous serions dans le deuxième cas).
On a donc prouvé que Pétait le centre de gravité de (ABC). Mais alors ∆passe par D, car O∈∆.
Nous sommes donc dans le premier cas.
En conclusion, |G|= 1 + 3 + 8 = 12.2
Théorème 1.3 (Structure) G'a4.
Preuve :
L’action de Gpermute les sommets de Tdonc on a un morphisme de ϕ:G−→ S4. Comme
(−→ OA, −−→ OB, −−→ OC)est une base de R3, et que les éléments de Gsont linéaires, ϕest injectif.
Comme Gcontient les rotations d’angle 2π
3, et d’axes OA,OB,OC,OD, on en déduit que Imϕ
contient tous les 3-cycles. Imϕcontient donc a4, et y est égale par cardinalité. 2
1

1.2 Le cube
Remarque 1.4 Rappelons que le cube est un polyèdre régulier à 8sommets, 6faces (carrés identiques),
et 12 arêtes de même longueur.
Soit Gle groupe des isométries directes du cube C= [1,2,3,4,10,20,30,40], avec x0symétrique de x
par rapport à Ocentre de C. Ici encore, Gstabilise les points extrémaux donc il stabilise O.
Théorème 1.5 (Ordre) Gest un groupe à 24 éléments.
Preuve :
Soit g∈G.
– Supposons que l’axe passe par l’un des sommets, disons 1. Alors l’axe est (1,10).ginduit une
rotation du plan (2,4,30). Comme 2,4et 30sont les seuls points à distance minimale de 1, cette
rotation les stabilise. On en déduit que gest une rotation d’angle 2π
3ou 4π 3. On obtient ainsi 4
groupes cycliques d’ordre 3, et donc 8éléments d’ordre 3.
– Supposons que l’axe de gcoupe une arête. Alors elle la coupe en son milieu, ainsi que l’arête opposée.
Il y a donc 6axes possibles, qui donnent chacun des rotations d’angle π. D’où 6éléments d’ordre 2.
– Supposons que l’axe de gcoupe une face. Alors il la coupe en son centre de gravité, ainsi que la
face opposée. On obtient donc 3axes, qui donnent chacun un groupe cyclique d’ordre 4. D’où 3
éléments d’ordre 2et 6éléments d’ordre 4.
En conclusion |G|= 1 + 9 + 14 = 24.2
Théorème 1.6 (Structure) G'S4
Preuve :
Remarquons tout d’abord que les distances possibles entre les sommets sont 1,√2et √3.
– Comme √3n’est obtenu que pour les paires de sommets opposés, on en déduit que Gagit sur les
quatre diagonales Dx= (x, x0). D’où un morphisme ϕ:G−→ S4.
– La rotation d’angle π
2et d’axe orthogonal à la face (1,2,3,4) montre que l’image de ϕcontient
le 4-cycle (D1, D2, D3, D4). De même, en considérant la rotation d’angle πet d’axe passant par le
milieu de (1,2), on voit que la transposition (D1, D2)est dans l’image de ϕ. Ainsi, ϕest surjectif,
et bijectif par cardinalité. 2
1.3 L’octaèdre
Remarque 1.7 Rappelons que l’octaèdre régulier est un polyèdre à 6sommets, 8faces (triangles équila-
téraux identiques), et 12 arêtes. Comme l’octaèdre est le dual du cube, son groupe d’isométries directes
est également isomorphe à S4.
1.4 Le dodécaèdre
Remarque 1.8 Rappelons que le dodécaèdre régulier est un polyèdre à 20 sommets, 12 faces (pentagones
réguliers identiques), et 30 arêtes de même longueur. En outre, chaque sommet appartient à 3arêtes, et
à3faces.
On note Gle groupe des isométries directes de D, dodécaèdre régulier. Ici encore, Gpermute les
sommets, et stabilise le centre de gravité Ode D.
Théorème 1.9 (Ordre) Gest groupe à 60 éléments.
Preuve :
Soit g∈G.
2

– Si l’axe de gpasse par le centre d’une face, ginduit une rotation sur le plan de cette face, isométrie
du pentagone régulier. On obtient ainsi 6groupes cycliques d’ordre 5, d’où 24 éléments d’ordre 5.
– Si l’axe de gpasse par le milieu d’une arête, gest une rotation d’angle π. On obtient ainsi 15
éléments d’ordre 2.
– Si l’axe de gpasse par un sommet, gstabilise les 3points à distance minimale de ce sommet. g
induit alors une rotation dans le plan de ces 3points, donc c’est une rotation d’angle 2π
3ou 4π 3.
D’où 20 éléments d’ordre 3.
En conclusion, |G|= 1 + 15 + 20 + 24 = 60.2
Théorème 1.10 (Structure) G'a5.
Preuve :
1. Solution géométrique
– On note (Ci)la famille des cinq cubes inscrits dans D(chaque point de Dappartient à deux
de ces cubes, et son symétrique appartient à ces deux mêmes cubes).
– Par des considérations de distances minimales, on observe que Gagit sur l’ensemble de ces
cubes. D’où un morphisme de ϕ:G−→ S5.
– En considérant la rotation d’angle 2π
5à travers une face de D, on voit que Imϕcontient tous
les cycles d’ordre 5.
– En particulier, a5est contenu dans l’image de ϕ, et en fait égal par cardinalité.
– Supposons que g∈Gfixe chacun de ces cubes, avec g6=e. Alors gest une rotation d’angle
π,2π
3,4π 3(cf. le groupe d’isométries du cube). Si gest d’angle π, son axe passe par le milieu
d’une arête du dodécaèdre, et ne peut pas laisser invariant chacun des cubes. Si gest d’ordre
3, l’axe de gest une diagonale du dodécaèdre, et gne peut stabiliser chacun des cubes. ϕest
donc injective. 2
2. Solution arithmétique
– Comme a5est le seul groupe simple d’ordre 60, il suffit de montrer que Gest simple. On va
utiliser le fait que tout sous-groupe distingué est réunion de classes de conjugaison.
– Si toutes les sommes non triviales de cardinaux de classes de conjugaison ne divisent pas G,
alors c’est gagné. Calculons donc ces cardinaux, et toutes les sommes possibles.
– Les éléments d’ordre 2sont clairement tous conjugués dans G.
– Les sous-groupes d’ordre 3(respectivement 5) sont deux à deux conjugués car ce sont des
stabilisateurs et que Gagit transitivement sur les sommets (respectivement les faces).
– Soit Pun sommet et ρrotation d’angle 2π
3dans le stabilisateur de P. C’est aussi la rotation
d’angle 4π
3du stabilisateur de P0, symétrique de Ppar rapport à O. On en déduit que ρ∈
Stab(P)est conjuguée à ρ2∈Stab(P0). Finalement, tous les éléments d’ordre 3sont conjugués
dans G.
– Les éléments d’ordre 5ne peuvent pas former une seule classe, car 24 ne divise pas 60. Soit ρ
élément d’ordre 5. Comme ci-dessus, ρ(respectivement ρ2) est conjuguée à ρ−1(respectivement
ρ3). Ainsi, ils forment au plus deux classes, et donc exactement deux.
– Il suffit maintenant de prouver qu’il est impossible d’obtenir 2,3,4,5,6,10,12,15,20,30
sous la forme s= 1 + 15a+ 12b+ 12c+ 20davec a, b, c, d ∈ {0,1}. Si b=c= 0, on obtient 1,
16,21 et 36. Si b= 0 et c= 1 (ou vice-versa), on obtient 13,28,33 et 48. Si b=c= 1, on
obtient 40,45,60.2
1.5 L’icosaèdre
Remarque 1.11 Rappelons que l’icosaèdre régulier est un polyèdre à 12 sommets, 20 faces (triangles
équilatéraux identiques) et 30 arêtes. Comme l’icosaèdre est le dual du dodécaèdre, son groupe d’isométries
directes est également isomorphe à a5.
3

2 Sous-groupes finis de SO(3)
Soit Gsous-groupe fini de SO3non trivial. On s’intéresse aux axes des éléments de G.
Définition 2.1 (Pôles d’une rotation)
Si ρ∈SO(3) et ρ6=Id, son axe coupe la sphère unité de R3en deux points pet p0, appelés pôles de la
rotation.
Notation 2.2 On notera X={pôles de ρ;ρ∈G\ {Id}}.
Par hypothèse, Xest fini. En outre, Gagit sur Xet pour tout p∈X, il existe h∈G\ {Id}tel que
ghg−1(g(p)) = g(p)pour tout g∈G.
2.1 Détermination du nombre d’orbite de G dans X
Notation 2.3 On note Nle nombre d’orbites de Gdans X.
Proposition 2.4 Nest égal à 2ou 3.
Preuve :
On va utiliser : N=1
|G|X
g∈G|Fix(g)|(Burnside)
–|Fix(g)|=½|X|si g=Id
2sinon =⇒N=1
|G|(|X|+ 2(|G| − 1))
– On choisit xidans chaque orbite Oi. Alors, en notant Gi=Stab(xi), on a
|X|=X|Oi|=X|G|
|Gi|(2.1)
N=
N
X
i=1
1
|Gi|+ 2 µ1−1 |G|¶(2.2)
N
X
i=1 µ1−1
|Gi|¶= 2 µ1−1 |G|¶(2.3)
– Comme |G|>2(par hypothèse), 1
262³1−1 |G|´<1. Or |Gi|>2(contient xiet x0
i), donc
N
26
N
X
i=1
(1 −1
|Gi|)< N. On en déduit 1< N et N
2<2, d’où N∈ {2,3}.2
2.2 Cas de deux orbites
Théorème 2.5 Si l’action de Gsur Xpossède deux orbites, alors Gest cyclique.
Preuve :
Ici, N= 2. Alors
2|G|= (|X|+ 2 (|G| − 1)) = (|O1|+|O2|+ 2 |G| − 2)
On en déduit |O1|+|O2|= 2 : chaque orbite est réduite à un élément. Il n’y a donc que deux pôles
p, p0, et Gest formé de rotations d’axe (pp0).Gest donc isomorphe à un sous-groupe fini de SO(2) :
Gest cyclique. 2
4

2.3 Cas de 3orbites
Théorème 2.6 Si l’action de Gsur Xpossède trois orbites, alors les cardinaux des stabilisateurs sont
nécessairement de la forme : (2,2, n),(2,3,3),(2,3,4) ou (2,3,5). Le cardinal de Gsera alors respecti-
vement égal à 2n,12,24, ou 60.
Preuve :
On prend des représentants x,y,zdes trois orbites, avec |Gx|6|Gy||Gz|.
Par Burnside, 1 + 2
|G|=1 |Gx|+1 |Gy|+1 |Gz|.
– Si |Gx|>3alors 1 + 2
|G|61 3+1 3+1 3= 1. C’est absurde, car Gest fini. Comme |Gx|>2, on a
|Gx|= 2.
– Si |Gy|= 2, alors |G|= 2 |Gz|= 2n.
– Si |Gy|= 3 alors 1
|Gz|=1 6+2 |G|>1 6. On en déduit 36|Gz|65.
– Si |Gy|>4alors 1 + 2
|G|61 2+1 4+1 4= 1, ce qui est absurde.
On calcule ensuite |G|avec la formule de Burnside dans chaque cas. 2
Théorème 2.7
Supposons que les cardinaux des stabilisateurs soient de la forme (2,2, n). Alors Gest isomorphe au
groupe des isométries du polygone régulier à néléments (autrement dit, G'D2nest le groupe diédral
d’ordre 2n).
Preuve :
– L’orbite de zpossède deux éléments. Soit gstabilisant z, alors gstabilise aussi z0. Le stabilisateur
de zest donc un sous-groupe d’ordre nde SO(2) : il est cyclique.
– Soit ρun générateur de Gz, et considérons P= (ρi(x))06i6n−1. Pour n6= 2, on obtient néléments
distincts qui forment l’orbite de x. En effet, si ρi(x) = ρj(x)pour i6=j, alors xest stabilisé par
ρj−i, rotation non-triviale d’axe (zz0), d’où x∈ {z, z0}. C’est absurde car Gxet Gzn’ont pas le
même ordre (cf. n6= 2). Pforme donc un polygone régulier à nsommets dans le plan z⊥. Comme
les ρi(x)forment une orbite sous G,Gagit sur P, et Gest le groupe des isométries de P.
– Si n= 2, deux cas sont possibles. Soit G=©Id, ρ, ρ2, ρ3ª, et Gest cyclique (absurde) soit ρest
d’angle π. Dans ce cas, si (x, x0)n’est pas orthogonal à (z, z0), on obtiendrait au moins trois points
dans l’orbite de x(absurde car n= 2 impose à cette orbite d’être réduite à {x, x0}). Ainsi, (x, x0),
(y, y0), et (z, z0)forment une base orthonormée de R3. Dans cette base, on obtient
G= I3,
−100
0−1 0
0 0 1
, −1 0 0
010
0 0 −1
,
1 0 0
0−1 0
0 0 −1
Finalement, G'D4.
2
Théorème 2.8 Si les cardinaux des stabilisateurs sont de la forme (2,3,3) alors Gest isomorphe au
groupe des isométries directes du tétraèdre régulier.
Preuve :
L’orbite de zest de cardinal 4, et Gzest un groupe cyclique d’ordre 3engendré par ρ.
– On considère u∈ Ozdistinct de zet z0. Alors u,ρ(u)et ρ2(u)sont distincts (les seuls points fixes
de ρet ρ2étant zet z0). Ce sont les sommets d’un triangle équilatéral dans un plan orthogonal à z.
– On en déduit que Oz=©z, u, ρ(u), ρ2uª. En outre kz−uk=kz−ρ(u)k=kz−ρ2(u)k.
– En effectuant le même raisonnement sur u, on obtient :
Ou=©u, z, ρ(u), ρ2uªet ku−zk=ku−ρ(u)k=ku−ρ2(u)k.
–©u, z, ρ(u), ρ2uªest donc un tétraèdre régulier sur lequel Gagit par isométrie. On en déduit que G
est isomorphe à un sous-groupe de a4. On conclut par cardinalité. 2
5