TP n°1 : LES LENTILLES MINCES CONVERGENTES

TP Physique - Spécialité Page 1 © F. Arnould – Lycée M France EPINAL - http://physiquark.free.fr
TP n°1 : LES LENTILLES MINCES CONVERGENTES
Objectifs :
- Rappeler les généralités sur la propagation de la lumière
- Déterminer la façon dont se forme l'image à travers une lentille mince convergente par expérimentation et par construction
- Réaliser le tracé sur papier des rayons particuliers dans le cas d'une lentille mince convergente.
- Déterminer expérimentalement les lois de focométrie puis les énoncer
1 – Rappels sur la propagation de la lumière
1.1 - Quelques définitions
OBJET :
On appelle objet un bloc de matière. Cela comprend aussi bien les astres (étoiles, planètes ) que les objets terrestres (arbres,
tables, chaises, etc...). On peut les classer en deux catégories :
Les objets lumineux par eux-mêmes (étoiles, lampes et enseignes lumineuses etc..) s’opposent aux objets non lumineux par eux-
mêmes (ainsi la lune est-elle un objet (bloc de matière) non lumineux par lui-même (sinon on verrait un disque et non pas un
croissant).
IMAGE :
Par opposition une image est quelque chose d’impalpable.
C’est un signal détecté par l’oeil mais avec lequel on ne peut avoir de contact physique. Les images se classent en deux
catégories.
Les images réelles sont des images que l’on peut voir et recueillir réellement sur un écran.
Ainsi une diapositive est un objet non lumineux par lui même. En l'éclairant fortement, il joue le rôle d'un objet lumineux dont on
peut faire l'image sur un écran ou sur sa main mais sans ressentir un contact physique.
A l’inverse les images virtuelles sont des images perçues par l’oeil mais que l’on ne peut recueillir sur un écran.
1.2 - Expérience n°1 : expérience des 2 bougies
Sur une table, dressons une vitre de faible épaisseur en position rigoureusement verticale. De part et d’autre, en position
symétrique par rapport au plan de la vitre, disposons deux bougies de même taille et allumons la bougie située du côté de
l’observateur. Changer la position d'observation.
✎1 Que peut-on remarquer ?
1.3 – Propagation de la lumière
Dans un milieu transparent et homogène (ainsi que dans le vide), la lumière se propage suivant des lignes droites à partir
de la source.
Ceci peut être mis en évidence au moyen de deux expériences assez simples à réaliser. L'une consiste à étudier l'ombre portée,
l'autre à utiliser une chambre noire.
Un rayon lumineux peut-être « brisé » ou « éparpillé »
Une surface réfléchissante, plane, modifie le trajet de la lumière en la renvoyant
dans une direction privilégiée.
Ce phénomène est la réflexion de la lumière.
L'angle d'incidence est égal à l'angle de réflexion.
La lumière subit un brusque changement de direction en traversant la surface de
séparation de deux milieux transparents.
Ce phénomène est la réfraction de la lumière.
Ces deux phénomènes obéissent aux lois de Decartes.
- La première loi de Descartes dit que le rayon réfléchi et le rayon réfracté
sont tous les deux dans le plan d’incidence.
- La seconde que l’angle de réflexion est égale à l’angle d’incidence.
- La troisième loi concerne la réfraction : pour un angle d’incidence i1 par
rapport à la normale, l’angle de réfraction i2 est tel que n1.sin(i1)=n2.sin(i2) , où
n1 et n2 sont les indices du premier et du second milieu.
La lumière ne peut traverser les corps opaques (métal, corps humain...). Une partie de la lumière est alors renvoyée dans toutes les
directions. La lumière est également "éparpillée" en traversant certains corps translucides (papier calque, ...).
Ce phénomène est la diffusion de la lumière.
REFLEXION
incident réfléchi
REFRACTION
Incident
i1
Réfracté
i2

TP Physique - Spécialité Page 2 © F. Arnould – Lycée M France EPINAL - http://physiquark.free.fr
2 – Les lentilles minces convergentes
2.1 - Définitions
Une lentille est un milieu transparent limité par deux surfaces sphériques
(ou une surface sphérique et une surface plane).
Une lentille est mince si son épaisseur au centre e est petite devant les
rayons de courbure R1 et R2.
Le centre de la lentille est un point appelé centre optique et noté O.
La droite D joignant les centres de courbure est l'axe optique de la lentille.
D est le diamètre d'ouverture.
2.2 - Symbolisation
Le symbole indique les deux
sens positifs choisis par
convention sur les axes horizontal et vertical. Dans toutes les constructions à venir la
lumière se propagera de la gauche vers la droite dans le sens positif horizontal.
2.3 – Tracé d'un rayon traversant une lentille
Un rayon lumineux qui traverse une lentille subit deux réfractions : à l'entrée de la lentille (de l'air dans le verre) et à la sortie (du
verre dans l'air). On prendra n2 = 1 (air) et n1 = 1,52 (verre)
✎2 Compléter le schéma suivant en utilisant la 3° loi de Descartes. Faire les calculs utiles.
2.4 – Observations d'un faisceau traversant la lentille dans plusieurs cas
On réalise les expériences suivantes :
Les traits correspondent à la direction des rayons lumineux parvenant sur la lentille.
✎3 Compléter les schémas et conclure. En particulier, justifier le terme de lentille
convergente à partir de l'expérience a.
2.5 - Conclusion
✎4 Compléter :
Une lentille mince convergente est caractérisée par - un __________________O,
- un __________________ D,
- un foyer objet F
- un foyer image F ' _______________ de F par rapport à O.
La distance focale f ' d'une lentille est la mesure algébrique
OF '
de la distance OF ':
f '=OF '
(f ' > 0 )
La vergence C d'une lentille vaut :
C=1
OF '
avec C en dioptrie ( d ) si f ' en mètre (m).
2.6 - Application
✎5 Calculer la vergence d'une lentille de distance focale f ' = 12 cm.
axe optique
R1
D
C1C2
R2
e
D
+
+
O
Axe optique
Centre optique
Rayon 1
Rayon 2
n2n2
n1
+
O
+
O
+
O
Exp a.
Exp b.
Exp c.

TP Physique - Spécialité Page 3 © F. Arnould – Lycée M France EPINAL - http://physiquark.free.fr
3 – Etude expérimentale d'une lentille mince convergente
3.1 - Dispositif expérimental
On dispose d’un banc d’optique,
système permettant d’aligner sur
un axe gradué les divers
systèmes utilisés.
Placer la lanterne de façon à
faire coïncider la lettre F avec
le zéro du banc gradué, la
lentille de 3 d sur son support et
l'écran comme sur le schéma ci-
contre.
L'objet est la lettre F (hauteur AB = 9 mm) : il est éclairé par la lampe. L'objet est positionné au zéro du banc d'optique.
3.2 - Mesures
Pour les distances objet - lentille 46,0 cm , 40,8 cm, 50,0 cm... données dans le tableau, rechercher la position de l'écran pour
laquelle on obtient une image nette de la lettre F.
✎6 Compléter le tableau ci-dessous (attention, on travaille en valeurs algébriques !) :
Les colonnes grisées sont à compléter par calcul après les mesures.
OA
(m)
AA '
(m)
A ' B '
(mm)
Taille de l'image
par rapport à
l'objet
Sens de l'image
par rapport à
l'objet
OA'
(m)
1
OA
(m-1)
1
OA'
(m-1)
-0,46
-0,48
-0,50
-0,52
-0,54
-0,56
-0,58
-0,60
-0,70
-0,75
3.3 - Interprétation
✎7 Lorsque l'on rapproche l'objet de la lentille (ou inversement), l'image se rapproche-t-elle ou s'éloigne-t-elle la lentille ?
Comment varie alors la taille de l'image par rapport à l'objet ?
✎8 Tracer le graphe
1
OA'
en fonction de
1
OA
avec l'échelle 1 cm pour 0,1 m-1. Attention
1
OA
toujours négatif !
✎ 9 Déterminer les caractéristiques de la courbe obtenue. En déduire une relation entre
1
OA'
,
1
OA
et
1
OF ' =1 f '
.
3.4 – Conclusion : formules de conjugaison et de grandissement
✎ 10 Une lentille de centre optique O et de distance focale f ' donne d'un point objet A situé sur l'axe optique un point image
A', conjugué de A, dont la position sur l'axe est donné par la relation de conjugaison :
✎ 11 Le grandissement g de l'image par rapport à l'objet est défini par :
= A' B'
AB =OA' OA
LANTERNE
Banc gradué
Ecran
Lentille et diaphragme
A
B
AB = 9 mm
OA'
 d
Faire coïncider avec la graduation zéro

TP Physique - Spécialité Page 4 © F. Arnould – Lycée M France EPINAL - http://physiquark.free.fr
4 – Construction de l'image donnée par une lentille mince
4.1 - Introduction
Point objet: point situé à l'intersection des rayons incidents ou de leur prolongements.
Point image: point situé à l'intersection des rayons émergents ou de leur prolongements.
On obtient une image de qualité, si à chaque point objet correspond un point image. La lentille
est alors utilisée " dans les conditions de Gauss".
Dans ces conditions, tout rayon incident passant par le foyer objet F ressort parallèlement à l'axe optique. Tout rayon incident
parallèle à l'axe optique émerge en passant par F'. De plus, tout rayon passant par le centre O de la lentille n'est pas dévié.
4.2 – Constructions (travail à faire)
Cas d'un objet à distance finie de la lentille
✎ 12 Placer F' puis construire l'image notée A'B' de l'objet AB. Caractériser l'image (taille, sens, position). Construire ensuite
la marche d'un faisceau lumineux issu de B et couvrant la lentille du bord supérieur au bord inférieur.
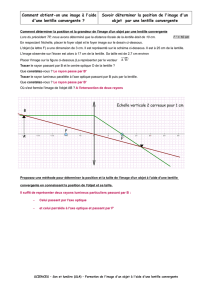
✎ 13 Dans quel plan particulier est situé l'objet AB ? Placer F' puis construire l'image notée A'B' de l'objet AB . Caractériser
l'image A'B' (taille, sens, position).
✎ 14 Placer F' puis construire l'image notée A'B' de l'objet AB . Caractériser l'image A'B' (taille, sens, position).
Cas d'un objet situé à l'infini
L'objet AB est placé à gauche "à l'infini": on suppose alors que les rayons issus du point B arrivent tous parallèles entre-eux donc
inclinés d'un même angle par rapport à l'axe optique.
✎ 15 Placer F' puis construire et caractériser l'image A'B'.
✎ 16 Sur le schéma de la question 12, placer les triangles homothétiques puis à l'aide du théorème de Thalès, retrouver la
relation de conjugaison.
Point objet Point image
O
F
B à l'infini
A
B
O
F
Cas OA > 2.f '
A
B
O
F
Cas OA = f '
A
B
O
F
Cas OA < f '