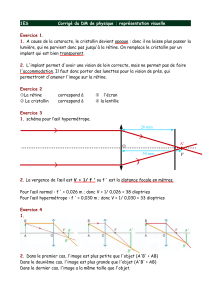
Rétine axe optique f > 0 Cristallin

Correction des défauts de l’œil (énoncé modifié !)
Chez un myope, l'image d'un objet « à l'infini » se forme devant la rétine lorsque le cristallin est au
repos. Calculer δ, la distance entre la rétine et la position de l'image non corrigée.
Soit fC la distance focale du cristallin au repos (fC > 0), a la distance entre le cristallin et la rétine
(a = 2,2 cm) et t la distance entre le verre correcteur et le cristallin (t = 1,5 cm). On appellera f la
distance focale du verre correcteur ; selon le défaut à corriger, on utilisera une lentille convergente
ou divergente de distance focale f = ± 1 m. Les verres correcteurs ont pour effet de déplacer l'image
afin qu'elle se forme exactement sur la rétine.
1°) oeil myope
a) Formation de l’image par l’œil :
a
Rétine
axe optique
f> 0
C
δ
Cristallin
f
1
q
1
p
1=+ ⇒
C
f
1
a
11 =
δ−
+
∞, donc δ = a - fC

b) Correction de la myopie :
Le cristallin est « trop convergent », il faut donc lui associer une lentille divergente.
La distance focale de la lentille correctrice est donc f1 = -1 m.
t
a
Rétine
f
1
axe optique
f
C
(les distances indiquées sur le schéma ne sont pas tracées à l’échelle !)
Pour que l’image se forme bien au niveau de la rétine, il faut que la distance focale-image du
système résultant de l’association des deux lentilles corresponde à la distance entre le cristallin et la
rétine, soit fi = a.
Avec f ⇒
ft f
tf f
i=−
−−
21
12
() δ−==
−−
−
=affoù,
fft
)ft(f
aC2
21
12
On a donc
()(
()
)
δ−−−
−δ−
=
−−
−
=aft
fta
fft
)ft(f
1
1
C1
1C
a⇒
(
)
(
)
(
)
(
)
11 ftaaafta
−
δ
−
=
δ
−
−
−
⇒ et
()
11 ftafta²a −+δ=δ−δ+δ=
()
1
fta
²a
−+
=δ
⇒ δ = 0,047 cm en remplaçant par les valeurs numériques données.
Autre méthode ( application de la loi de Descartes) :
Pour la première lentille :
11 f
1
q
11 =+
∞ ⇒ q1 = f1 = -1 m négatif , donc à gauche de la lentille 1!
Pour la 2ème lentille (cristallin) ⇒ p2 = t + 1m = 101,5 cm
⇒ q2 = a, pour que l’image se forme sur la rétine
⇒
222 f
1
q
1
p
1=+ ⇒ f2 = 2,153 cm = fC
Si l’œil n’est pas corrigé, on a
δ
−= a
C
f ⇒ δ = 2,200 – 2,153 = 0,047 cm.
-2-