DEVOIR SURVEILLE DE PHYSIQUE N°3 Problème

Janson de Sailly PC*1 / PC*2 / PC Devoir surveillé de physique n°3 J-C G
1
PC*1 / PC*2 / PC DEVOIR SURVEILLE DE PHYSIQUE N°3
5 novembre 2016
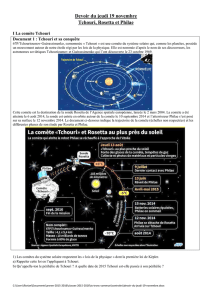
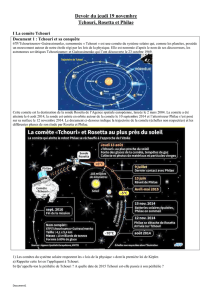
Problème 1 TCHOURI, ROSETTA ET PHILAE
Tchourioumov-Guérassimenko, ou simplement « Tchouri » pour les intimes, est une comète du système solaire,
ainsi nommée d'après le nom de ses découvreurs les astronomes soviétiques (actuellement ukrainiens) Klim
Ivanovitch Tchourioumov et Svetlana Ivanovna Guérassimenko, qui ont observé l'astre sur leurs plaques
photographiques le 23 octobre 1969 à Kiev.
Comme pour beaucoup de comètes, la trajectoire de Tchouri a sensiblement évolué au cours du temps, mais
depuis 1959, elle s’est stabilisée. La comète décrit actuellement une trajectoire elliptique dont le soleil est
l’un des foyers, et caractérisée par un périhélie de 1,24 ua et un aphélie de 5,68 ua.
Par ailleurs, la comète est animée d’un mouvement de rotation propre de
période
TTch =
12,4 h.
L’Agence spatiale européenne initie en 1993 un ambitieux projet d’exploration
de comètes. Le 2 mars 2004, la sonde Rosetta est lancée avec pour mission de
s’approcher de la comète lorsque celle-ci serait au périhélie de sa trajectoire.
Rosetta libérerait alors un robot de 100 kg, l'atterrisseur Philae qui devrait
se poser sur la surface de Tchouri pour des analyses in situ.
La sonde Rosetta atteint la comète le 6 août 2014 et le 10 septembre
se met sur une orbite circulaire de rayon
r
1
= 30 km pour une phase
d'observation. Les premières photos de Tchouri permettent de
découvrir un astéroïde de 1,0.1013 kg ayant, selon certains, plus ou
moins une forme de canard !
A partir du 8 octobre 2014, Rosetta parcourt une orbite elliptique
avec un apocentre A situé à la distance
r
a
= 20 km du centre T de la
comète et un péricentre P défini par
r
P
= 10 km.
Le 15 octobre, la vitesse de la sonde est modifiée à l’aide de
propulseurs constitués de tuyères éjectant des gaz. Ce dispositif
est utilisé alors que Rosetta est au péricentre de sa trajectoire, et
amène la sonde sur une orbite circulaire de rayon
rp
= 10 km.
Pour préparer la libération de Philae, la sonde change encore
d’orbite et s’éloigne de la comète.
Le 12 novembre à 8h35 : l’atterrisseur est largué par le
vaisseau mère Rosetta alors à 20,7 km d’altitude au dessus de
la comète. Il chute vers son objectif durant environ 7 heures à
la vitesse moyenne de 0,90 m.s–1. A la surface de la comète,
« il ne pèse que 2 g ! »
A 15h34 : impact de l’atterrisseur sur le sol de la comète,
avec un angle de 15° par rapport à la verticale.
Près de 5 minutes après le contact avec la surface, les
caméras embarquées doivent commencer à réaliser le
panorama à 360° du paysage qui entoure Philae.
Cependant les images reçues sont floues.
En fait, le système propulsif à gaz froid qui doit plaquer Philae au sol ne s’est pas activé et les harpons n’ont
donc pas été déclenchés.
Le robot a alors rebondi mais, les trois pieds du train d’atterrissage étant équipés d’absorbeurs de chocs, sa
vitesse a heureusement été divisée par deux.
Emblème de la mission Rosetta
La comète Tchouri
L’atterrisseur Philae

Janson de Sailly PC*1 / PC*2 / PC Devoir surveillé de physique n°3 J-C G
2
A 17h25 : second impact. L’atterrisseur vient de toucher le sol à nouveau. Le lendemain, le centre de
contrôle annonce dans la presse que Philae est remonté à près de 1 km d’altitude et finalement retombé à
plus de 1 km de son premier point d’impact. Le second rebond s'achève contre une paroi.
L'agence spatiale met fin à la mission de Rosetta le 30 septembre 2016 en écrasant l'engin sur le sol de la
comète.
Klim Tchourioumov est décédé le 14 octobre 2016.
Données
- L’unité astronomique ou ua est couramment utilisée pour exprimer les distances entre les objets célestes
du système solaire. Elle correspond à la distance moyenne de la Terre au Soleil soit 1 ua ≈1,5.108 km.
- Le périhélie et l’aphélie sont les points respectivement le plus proche et le plus éloigné d’une orbite
elliptique dont le soleil, helios, est le foyer.
D’une façon générique, on parle de péricentre et d’apocentre.
- constante gravitationnelle : G = 6,67.10–11 USI.
- masse du soleil :
MS=2.1030
kg
- masse de la terre :
MT=
6.1024 kg
- masse de la sonde Rosetta :
mRos
= 1500 kg
- rayon de la terre :
RT=6400
km
Questionnaire
1) Quelle est la durée de la période de Tchouri ?
2) Pour quelle(s) raison(s) l’orbite des comètes peut-elle évoluer au cours des siècles ?
3) Que peut-on dire simplement de la valeur de l’énergie mécanique de la comète ?
4) Malgré sa forme canardesque, la comète pourra être décrite, pour tous les calculs, par une boule homogène
de masse volumique kg.m-3 uniforme
Justifier l’intérêt de cette modélisation, et déterminer le rayon
RTch
de la boule équivalente à la comète.
5) Expliquer qualitativement pourquoi des comètes se désagrègent en passant à proximité du soleil.
On évalue le terme de marée exercé par le soleil sur un corps céleste situé à la distance D :
Cmar =
2GM SRastre
D3
.
Estimer le terme de marée exercé par le soleil sur terre et sur la comète, puis comparer les aux pesanteurs
respectives sur ces astres. Commenter.
6) On définit l’accélération g de la pesanteur à la surface de Tchouri de la même façon que sur la Terre.
Peut-on considérer g à la surface de Tchouri comme uniforme ? Dans toute la suite du problème, on
identifiera le champ de pesanteur de la comète à son champ gravitationnel.
7) Peut-on considérer le champ gravitationnel de la comète uniforme lors de la chute du module Philae, suite
à son largage ?
8) Justifier que dans le référentiel Tchouricentrique R,(Tch) , que l’on définira, la trajectoire de la sonde,
assimilée à un point matériel R, reste plane pendant son mouvement sa phase de mouvement sans moteur
autour de Tchouri.
9) Calculer la vitesse
v1
et la période
T
1
de la sonde lorsqu’elle est en en orbite circulaire autour de la comète,
10) Exprimer l’énergie mécanique de la sonde sur l’orbite elliptique en fonction de
r
a
et
rp
et en déduire la
vitesse
vp
de Rosetta en P.
µTch =400

Janson de Sailly PC*1 / PC*2 / PC Devoir surveillé de physique n°3 J-C G
3
11) Quelle la variation de vitesse doit fournir la propulsion pour placer la sonde en orbite circulaire de
rayon
rp
?
12) Les courbes ci dessous représentent les évolutions temporelles de la distance de Philea au centre de la
comète pour différentes vitesses initiales de l’atterrisseur :
v0=0
m.s-1 ,
v0=0,15
m.s-1 ,
v0=0,30
m.s-1 ,
v0=0,45
m.s-1 ,
v0=0,60
m.s-1 ,
v0=0,75
m.s-1 ,
v0=0,90
m.s-1,
v0=1,05
m.s-1 ,
v0=1,20
m.s-1 .
La figure de droite est un zoom de celle de gauche pour les faibles distances.
Quelle est la vitesse verticale initiale communiquée à l’atterrisseur ?
13) Déterminer dans R,(Tch) la vitesse de Philae au moment de l’impact. L’étude de la chute serait-elle
significativement modifiée dans le référentiel lié à la comète ?
14) En supposant que le rebond de Philae s’est fait symétriquement à la verticale, justifier les valeurs
numériques indiquées dans le texte concernant ce rebond.
On pourra faire d’abord une hypothèse (beaucoup trop !) simpliste sur le champ de pesanteur de la
comète, puis y revenir a posteriori.
Problème 2 FREINAGE D’UN LINGOT SUR UN CONVOYEUR A ROULEAUX
Le problème consiste à étudier le déplacement d’un lingot sur un convoyeur à rouleaux.
Le solide S est un lingot métallique parallélépipédique homogène et caractérisé par ses dimensions :
longueur 2l, hauteur 2h, largeur b, sa masse M , et son barycentre G.
Ce lingot se déplace sur un convoyeur à rouleaux constitué d’un ensemble de rouleaux cylindriques
homogènes et identiques de rayon r. Chaque rouleau est susceptible de tourner autour de son axe.
Les axes des rouleaux sont parallèles, tous situés dans le même plan horizontal et distant de 2d.
Le moment d’inertie relativement à cet axe sera noté J.
On va s’intéresser à une phase de freinage du lingot.

Janson de Sailly PC*1 / PC*2 / PC Devoir surveillé de physique n°3 J-C G
4
Soit un repère Oxyz orthonormé ;
ex, ey, ez
désignent les vecteurs unitaires associés aux axes (Ox est
horizontal, Oy est vertical ascendant). Ce repère est lié au référentiel du laboratoire supposé galiléen. La
position de O est choisie de telle façon qu’à t = 0, le point G se situe sur la verticale de O.
On va considérer la situation pour laquelle le solide est en contact avec deux rouleaux particuliers, les
rouleaux n°1 et n°2 de centres respectifs les points O1 et O2 (on suppose 2l > 2d).
Le rouleau n°1 peut tourner librement autour de son axe horizontal, la liaison étant supposée parfaite.
Le rouleau n°2 est entrainé en rotation par un moteur extérieur non figuré, avec
!
ω2=ω2
!
uz
et une vitesse de
rotation est
ω2
> 0 constante au cours du temps. A l’instant initial, l’extrémité droite du solide se situe à la
verticale du point O2, la vitesse du solide est
X0=dX
dt (0)
> 0.
Les points de contact du solide sur les rouleaux sont notés respectivement I1 et I2. Le rouleau n°2 va donc
freiner le solide S et, à un instant
t=τ
, S va s’immobiliser ; la suite du mouvement ne sera pas considérée.
Le coefficient de frottement S/rouleau sera noté µ, il ne sera pas fait de distinction entre les coefficients de
frottement dynamique ou statique.
g
désigne le vecteur accélération de la pesanteur, soit
g=−g ey
. On note
X ( t )
, l’abscisse du point G à un
instant quelconque,
R1=T1 ex+N1 ey
,
R2=T2 ex+N2 ey
les actions des rouleaux sur S appliquées en I1 et I2
Dans la suite du problème, on supposera toujours que le mouvement du solide S s’effectue sans glissement
sur le rouleau n°1.
Pour les applications numériques, on donne l = 1m, d = 0,8 m, h = 0,2 m, r = 0,2 m, µ= 0,1 M =3500 kg,
J =20 kg.m2, g = 9,81m.s-2,
X0
= 0,442 m.s-1
1) Le vecteur vitesse de rotation du premier cylindre est noté
ω1 ez
.
Exprimer la relation de non glissement en I1. (relation 1).
2) Déterminer la vitesse de glissement de S sur le rouleau n°2 en fonction de
X
, r,
ω2
. Dans ces conditions,
quel est le signe de T2 ? Écrire la relation liant T2 et N2 (relation 2).
3) Etablir deux relations scalaires (relations 3 et 4) relatives au mouvement du solide S seul.
4) En considérant le rouleau n°1 seul, établir une relation faisant intervenir (entre autres)
dω1
dt
(relation 5).
5) On note
LG
le moment cinétique en G de S. Quelle est la valeur de
LG
? En déduire une relation liant
(entre autres)
N1,N2,T
1
et
T2
(relation 6).
On admettra que le théorème du moment cinétique scalaire peut s’appliquer à l’axe Gz, bien que mobile
mais passant par le centre d’inertie du solide, comme pour un axe fixe du référentiel d’étude.
Schéma : vue dans le plan vertical Oxy à l’instant t = 0 (les
flèches rondes indiquent le sens de rotation des rouleaux)

Janson de Sailly PC*1 / PC*2 / PC Devoir surveillé de physique n°3 J-C G
5
6) Déduire des relations précédentes une équation différentielle en
X ( t )
.
7) En comparant les valeurs numériques de
µh
et 2d, vérifier que cette équation est bien celle d’un
oscillateur harmonique de position d’équilibre
Xe=l−2d
, dont la pulsation peut se simplifier en
Ω ≈ 1
2d
µg
1+J
Mr2
⎛
⎝
⎜⎞
⎠
⎟
8) Etablir la loi
X ( t )
et décrire le mouvement de S à ses débuts (
Ωt<< 1
).
9) À l’instant
t=τ
, la vitesse de S s’annule (pour la première fois).
a) Établir l’expression de
tan Ωτ
en fonction de Ω, l, d et
X0
. Compte tenu de la valeur numérique de
tan Ωτ
, calculer l’amplitude maximale
Xm
du déplacement du point G. En déduire que le solide S est
toujours en appui sur le rouleau n°1 à l’instant
t=τ
.
b) Vérifier également que le mouvement de S reste bien « de roulement sans glissement » jusqu’à
l’instant
t=τ
.
10) Établir les expressions de
N1( X )
et
N2( X )
en fonction des constantes du problème. En considérant
la forme de ces fonctions, donner les conditions nécessaires pour qu’il n’y ait pas basculement du solide
S entre les instants t = 0 et
t=τ
.
11) Exprimer l’énergie cinétique
Ec( t )
de l’ensemble (solide S + rouleau n°1) en fonction des paramètres du
problème.
12) En déduire l’expression de
W
1
, travail reçu par l’ensemble (solide S + rouleau n°1) entre les instants t = 0
et
t=τ
. Quelle est la force qui fournit ce travail ?" est-il moteur ? résistant ?
13) a) Exprimer le travail fourni par le moteur d’entrainement au rouleau n°2 entre les instants t = 0 et
t=τ
.
b) Quel est le travail dissipé en chaleur les instants t = 0 et
t=τ
.
Problème 3 LE CRISSEMENT DE LA CRAIE
Lorsqu’on déplace une craie sur un tableau, il arrive qu’un son désagréable soit émis : la craie crisse.
On utilisera le modèle suivant : un pavé de masse m
est posé sur une table horizontale et relié par un point A
à un ressort de raideur k et de longueur à vide négligeable,
dont l’autre extrémité B est déplacée à vitesse constante V
par un moteur de telle sorte que son abscisse vérifie
xB( t ) =Vt +b0
. Le mouvement du pavé est repéré par
l’abscisse
x( t )
du point A et on note
l( t ) =xB( t ) −x( t )
la longueur du ressort à un instant t.
Le champ de pesanteur
g=−g uz
est uniforme, avec g =10 SI. Les actions de contact exercées par la table
sur le pavé se réduisent à une force de contact
R=T ux+N uz
satisfaisant aux lois de Coulomb avec un
coefficient de frottement statique fs et un coefficient de frottement dynamique fd : ces coefficients sont
supposés différents avec fd < fs.
On observe que le pavé se déplace vers la droite avec une alternance de phases de glissement et de non
glissement, appelé régime de stick and slip ou collé-glissé.
x
z
A
B
•
•