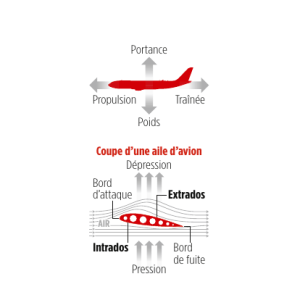
Équations de mouvement de l`avion

EQUATIONS DE MOUVEMENT D'UN AVION RIGIDE
STABILITÉ LONGITUDINALE ET LATÉRALE

SYSTÈMES DES AXES LIÉ À L'AVION
XY Z - Système d'axes lié à la Terre
XY Z - Système d'axes lié à l'avion a

CALCUL DES FORCES
(2ième Loi de Newton)
()
vm
dt
d
F
∑=
où
F - Somme des forces externes appliquées
m - Masse de l’avion
V - Vitesse vraie de l’avion
->
()
mu
dt
d
F=
()
mv
dt
d
F=
()
mw
dt
d
F=

CALCUL DES MOMENTS
(2ième Loi de Newton)
()
H
d
t
d
M
∑=
où
M - Somme des moments externes appliquées
m - Masse de l’avion
H - Moment d'impulsion
->
dt
dH
L= dt
dH
M= dt
dH
N=

CALCUL DES FORCES SUR UN AVION
δ m
r
X
Y
V
Z
δ m – masse d'un élément de l'avion
F
dt
d
mF ==∑∑ v
δδ