BERSIA Vincent

BERSIA Vincent.
Groupe O 1.
Ecrit disciplinaire de
mathématiques :
La notion d’angle
en CM1 et CM2.
Année 2009 / 2010.

2
L’écrit disciplinaire suivant analyse une séquence de géométrie ayant pour thématique la
notion d’angle. Cette séquence a été menée au cours de mon stage groupé 2 qui s’est déroulé dans
une classe de CM1 et CM2 à l’école élémentaire Condorcet 1 de Meaux du Vendredi 26 mars au
Vendredi 16 avril 2010.
La notion d’angle est abordée, d’après le Bulletin officiel de l’Education nationale du 19
juin 2008, en classe de CE1. En effet, les progressions dictées par le ministère de l’Education
nationale précisent qu’au cours élémentaire première année, les élèves apprennent à « percevoir et
reconnaître quelques relations géométriques comme l’alignement, l’angle droit, l’axe de symétrie et
les égalités de longueur». Par la suite, au cycle des approfondissements, les élèves doivent savoir :
Au CE2 :
- Utiliser en situation le vocabulaire côté, sommet, angle et milieu.
- Vérifier qu’un angle est droit en utilisant l’équerre ou un gabarit.
Au CM1, la notion d’angle est approfondie. Les élèves doivent :
- Comparer les angles d’une figure en utilisant un gabarit.
- Estimer et vérifier si un angle est droit, aigu ou obtus.
Au CM2, les compétences citées ci-dessus sont retravaillées puis complétées car les élèves doivent
être capables de reproduire un angle donné en utilisant un gabarit.
La séquence analysée dans cet écrit se décompose en sept séances (cf document p 13 et 14 :
fiche de préparation de séquence) et a pour finalité d’une part de travailler les objectifs imposés par
le cycle 3 et d’autre part de rendre plus évident la reproduction de figures géométriques pour ensuite
glisser vers la rédaction de programmes de construction.
L’écrit disciplinaire suivant analysera les deux premières séances de la séquence. Pour
chacune de ces deux séances mises en place dans la classe de CM1 et CM2, nous décrirons le ou les
objectifs visés par les activités, nous préciserons les points forts et les points faibles de chaque
séance et enfin, nous détaillerons les difficultés des élèves et les procédures de différenciation et de
remédiation pour pallier les difficultés des élèves.
Séance 1 :
Lorsque j’ai commencé cette première séance sur la notion d’angle, les élèves, qu’ils soient
en deuxième ou troisième année du cycle des approfondissements, possédaient déjà certains acquis
sur la notion. L’objectif affiché de cette séance était double. Il s’agissait tout d’abord de trouver une
définition géométriquement valable d’un angle puis, les élèves devaient comprendre que la
longueur des côtés d’un angle n’avait pas d’influence sur la mesure de cet angle. Pour parvenir à ces
deux objectifs, la séance a débuté par une mise en commun des connaissances des élèves sur la
notion d’angle. La quasi-totalité des élèves se représentait bien un angle mentalement mais la
difficulté de cet exercice a été pour les élèves de mettre des mots sur leurs représentations mentales
de l’angle. Malgré cette difficulté, certains termes permettant de donner une définition correcte d’un
point de vue géométrique sont apparus comme par exemple « sommet, arêtes, droites se coupent ».
L’apparition de ce vocabulaire géométrique très pertinent a été facilitée par le travail réalisé en
amont lorsque les élèves avaient abordé l’étude des différents polygones. Ainsi, les élèves ont réussi
à établir des inférences entre les notions et à réinvestir certaines connaissances. Néanmoins, à ce
stade du déroulement de la séance, aucun élève n’a été en mesure de formuler une définition

3
complète. La séance s’est donc poursuivie par une acticité de manipulation. En effet, tous les élèves
disposaient d’un polygone A (cf Page 8 «Polygones donnés aux élèves pour la séance 1 ») et d’un
autre polygone C ou D selon les capacités des élèves. Le travail des élèves consistait donc à trouver
les angles de la figure C ou D qui s’encastraient parfaitement dans les angles de la figure A. Les
élèves devaient donc essayer chaque angle du polygone C ou D dans chacun des angles du polygone
A. Lorsque deux angles s’emboîtaient parfaitement les élèves devaient renseigner le tableau ci-
dessous.
Angle de la
figure A.
Angle de la
figure C.
Angle de la
figure D.
A
B
C
D
E
F
G
H
I
La consigne de l’exercice a été comprise par les élèves. Cependant compléter le tableau a été
plus difficile. En effet, les élèves n’ont pas compris qu’il fallait reporter le numéro de l’angle de la
figure C ou D sur la même ligne que la lettre qui nomme les angles du polygone A. J’aurais dû
anticiper cette difficulté lors de la conception de cette séance. En effet, le tableau a été une difficulté
supplémentaire et surtout inutile pour les élèves. Il aurait sans doute été préférable de laisser les
élèves écrire une phrase eux-mêmes pour donner la réponse ou alors de leur donner un texte à trous
sous la forme :
« L’angle numéro ….. de la figure C s’encastre parfaitement dans l’angle ….de la figure A»
En dépit de cette difficulté, l’activité a été plutôt positive. En effet, les élèves étaient en
phase de recherche ce qui a permis d’apporter une vision plus concrète de ce que pouvait être un
angle. En outre, proposer aux élèves en difficultés un polygone avec moins d’angles à tester a allégé
la tâche des élèves d’un point de vue cognitif.
Néanmoins, le bilan de cette première séance laisse apparaître certains points faibles. Tout
d’abord, la tâche à accomplir pour les élèves était bien trop courte. De plus, cette séance de
découverte n’était pas assez fondée sur des activités de manipulations permettant aux élèves d’avoir
une image concrète d’un angle. Ce n’est que trop tard que je me suis rendu compte que je n’avais
pas assez fait manipuler les élèves pour qu’ils comprennent qu’un angle peut se définir comme une
ouverture, comme un écartement entre deux droites sécantes. Par conséquent, il était impossible
pour les élèves de trouver une définition d’un angle car le manque d’activité de manipulation dans
cette séance a empêché les élèves de passer d’une représentation concrète à une représentation
abstraite de la notion d’angle. Pour pallier cette difficulté, j’aurais dû utiliser « le compas d’angle ».
En effet, le compas d’angle est constitué de deux bandes de papier cartonné attachées entres elles
grâce à une attache parisienne. Ainsi, l’attache parisienne permet d’ouvrir et de fermer le compas
d’angle ce qui aurait sans aucun doute permis aux élèves de comprendre qu’un angle est une
ouverture, un espace qui peut s’agrandir ou se rétrécir entre deux droites ou segments.
Au final, aucune définition géométrique de la notion d’angle n’a émergé à la fin de cette
première séance. L’objectif de trouver une définition d’un angle n’était donc pas très pertinent pour
une première séance. La définition serait peut être venue plus naturellement en fin de séquence
après avoir rencontré, comparé et tracé des angles. Ainsi, cette première séance manquait de

4
manipulation pour les élèves afin qu’ils puissent passer plus facilement de la représentation
concrète d’un angle à sa définition abstraite.
Séance 2 :
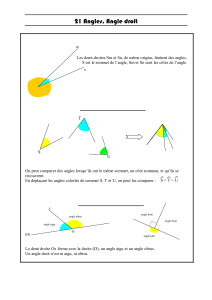
L’objectif de cette seconde séance était de percevoir dans la figure donnée en annexe de cet
écrit disciplinaire (cf document p 11 : Fiche élève. Les angles : Séance 2) des angles droits puis de
les vérifier en utilisant un gabarit d’angle droit, c'est-à-dire un angle droit tracé à la règle et à
l’équerre sur du papier calque (voir document p 12 : «Matériel utilisé au cours de la séance n°2 ».).
L’objectif consistait ensuite à trouver sur la même figure les angles aigus et les angles obtus.
Pour pallier les difficultés rencontrées par les élèves lors de la première séance, j’ai choisi de
commencer cette deuxième séance en présentant aux élèves le compas d’angle. J’ai tout d’abord
ouvert le compas d’angle de façon à décrire un angle droit et j’y ai posé dessus une équerre. Les
élèves ont rapidement compris que le compas d’angle formait un angle droit. J’ai donc poursuivi la
démonstration en fermant puis en ouvrant progressivement ce même compas d’angle et les élèves
ont trouvé qu’un angle pouvait se définir comme une ouverture entre deux droites. Ils ont ensuite
compris qu’il existait une multitude d’angles et que certains étaient plus ouverts que l’angle droit et
d’autres étaient plus fermés. Dès lors, les élèves possédaient les connaissances nécessaires pour
faire l’exercice proposé.
En effet, les élèves, munis d’un crayon à papier devaient coder sur la figure les angles qui
leur semblaient droits. Ensuite, sur un morceau de papier calque, les élèves ont tracé un angle droit.
Cet exercice, qui me semblait plutôt accessible pour des élèves de CM1 et CM2, a été au final plus
difficile que prévu. En effet, un grand nombre d’élèves a tracé l’angle droit sans équerre, à vue
d’œil, et était convaincu que leur angle était bien droit. Il a donc fallu faire le tracé de l’angle droit
sur le papier calque en groupe classe en écrivant au tableau les étapes de la construction et les outils
géométriques à employer. Il ne restait plus qu’à coder l’angle droit pour ensuite pouvoir vérifier sur
la figure si les angles perçus comme étant droits l’étaient réellement. Pour cela, les élèves ont
superposé les demi-droites et le sommet de l’angle droit sur les côtés de l’angle droit de la figure
pour s’assurer que les côtés des angles se superposaient parfaitement.
Je me suis demandé si je n’aurais pas dû utiliser, pour vérifier si les angles étaient bien
droits, un gabarit d’angle droit fabriqué en pliant une feuille A4 en deux et rabattant les côtés sur
eux-mêmes. Cette technique aurait sans doute évité les problèmes de construction de l’angle droit
sur le papier calque. Néanmoins, je pense que j’aurais eu du mal à justifier aux élèves que l’angle
formé par les pliages de la feuille est bien un angle droit. En outre, si ce gabarit favorise
incontestablement le tracé d’un angle droit, je trouve que le papier calque est plus efficace pour
vérifier les angles droits car il offre plus de visibilité et donc plus de précision lorsque les élèves
superposent les angles.
Une fois les angles droits vérifiés grâce au papier calque, la tâche des élèves consistait à
reconnaître les angles aigus et les angles obtus. Le vocabulaire « angle aigu et angle obtus » n’a pas
été donné tout de suite. A ce stade du déroulement de la séance, nous ne parlions encore que
d’angles moins ouverts (angle aigu) ou plus ouverts (angle obtus) que l’angle droit. Certains élèves
ont eu du mal à saisir la différence. Aussi, j’ai fourni à ces élèves un compas d’angle et je leur ai
demandé dans un premier temps de former avec cet outil un angle droit, puis de former un angle
moins ouvert que l’angle droit. Ils ont tous compris qu’il suffisait de fermer le compas d’angle et
qu’ainsi on obtenait un angle moins ouvert. La même manipulation a été effectuée pour les angles
obtus. Ensuite, nous avons testé sur la figure géométrique le compas d’angle ouvert en position
d’angle droit sur les angles aigus et obtus de la figure géométrique. Si les élèves devaient fermer le
compas pour que les bords de ce dernier se superposent sur les cotés de l’angle, les élèves
répondaient qu’il s’agissait d’un angle moins ouvert que l’angle droit et pouvaient donc le colorier

5
en vert. Ensuite, les élèves procédaient de même pour les angles obtus. S’ils ouvraient le compas
d’angle pour que ses bords se superposent sur les cotés de l’angle obtus, les élèves répondaient qu’il
s’agissait d’un angle plus ouvert que l’angle droit et le coloriaient donc en bleu.
La séance s’est terminée par la distribution d’une trace écrite aux élèves dans laquelle étaient
données la définition d’un angle ainsi que la définition d’un angle aigu et obtus.
Si les élèves ont trouvé assez facilement les angles droits et aigus et que très peu d’erreurs
ont été relevées au moment de la correction, il n’en demeure pas moins que les élèves ont éprouvé
plus de difficultés pour repérer les angles obtus. Je pense que cette difficulté peut s’expliquer par
deux facteurs :
D’une part, les élèves rencontrent plus souvent des polygones aux angles aigus que des polygones
aux angles obtus. Par exemple, les triangles sont trop souvent présentés aux élèves dans leur forme
prototypique, c'est-à-dire des triangles posés sur une de ses bases et dont les trois angles sont aigus
ce qui peut amener les élèves à croire qu’un angle est forcément moins ouvert qu’un angle droit.
D’autre part, la difficulté à repérer les angles obtus peut s’expliquer par le fait que, dans la figure
donnée aux élèves, il n’y avait que six angles obtus alors que les angles aigus et droits étaient plus
nombreux.
Je pense que j’aurais dû passer par une étape supplémentaire pour distinguer les angles aigus
et obtus. En effet, j’aurais certainement dû proposer aux élèves un échantillon de huit ou dix angles
aigus et obtus sur une feuille de papier et leur demander, par groupe de deux ou trois, de les classer
dans un tableau de deux colonnes en justifiant leur critère de classement. De cette façon, lors de la
mise en commun des classements, quelques groupes auraient peut être dit qu’il existait des angles
dont l’ouverture entre les deux demi-droites est grande et d’autres angles dont l’ouverture est plus
étroite. Il n’aurait donc suffit dès lors que de valider cette hypothèse et d’introduire le vocabulaire
spécifique d’angle aigu et d’angle obtus.
La durée d’activité des élèves au cours de cette séance constitue un autre point faible. En
effet, les tâches données aux élèves étaient bien trop brèves et je n’avais prévu aucun exercice
supplémentaire pour les élèves ayant fini plus tôt que les autres. Par conséquent, la gestion de la
classe s’est avérée beaucoup plus délicate.
Ainsi, l’analyse de ces deux séances sur la notion d’angle dans une classe de CM1 et CM2 a
permis de mettre en valeur les lacunes des séances mises en œuvre au cours du stage groupé en
responsabilité en cycle 3. Au premier plan de ces lacunes, il faut citer la trop faible activité de
manipulation proposée aux élèves lors de la première séance ce qui n’a pas permis aux élèves de
passer d’une représentation concrète à une représentation abstraite d’un angle pour pouvoir en
proposer une définition. La seconde lacune majeure de cette séquence est le manque d’exercice
proposé aux élèves. En effet, les exercices d’application auraient dû être plus nombreux afin de
placer les élèves en phase de recherche plus active que lorsqu’ils écoutent parler leur enseignant. Il
est donc impossible de se contenter d’une pédagogie frontale en croyant que les paroles de
l’enseignant sont acquises par l’ensemble des élèves de la classe.