Devoir en temps libre : autour du losange 1 Un quadrilatère dont les

Devoir en temps libre : autour du losange
Ce problème contient trois exercices indépendants et de difficulté croissante sur le thème du losange.
On démontrera notamment à l’aide des nombres complexes quelques résultats de géométrie bien connus depuis
le collège. A priori on ne s’autorise que les résultats proprement démontrés dans le cours de C.P.G.E. ; lorsqu’un
théorème vu dans le cycle secondaire sera nécessaire, l’énoncé le précisera explicitement.
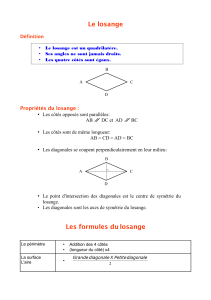
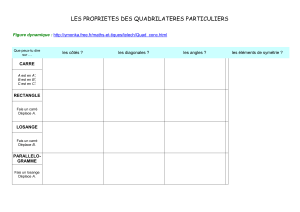
On rappelle qu’un losange est par définition un quadrilatère dont les quatre côtés sont de même longueur, et dont
tous les points sont deux à deux distincts.
Pour ces trois exercices, le plan est muni d’un repère orthonormé direct (O,~ i,~ j).
1. Dessiner un quadrilatère dont les quatre côtés sont de même longueur mais qui n’est pas un losange.
1 Un quadrilatère dont les diagonales se coupent en leur milieu et à angle
droit est un losange
Pour simplifier nous étudierons un quadrilatère dont un des sommet est l’origine. Soient donc A,B,Ctrois points.
Nous supposons que O,A,B,Csont deux à deux distincts et que les diagonales du quadrilatère OABC sont orthogo-
nales et se coupent en leur milieu. Le but est de démontrer que OABC est un losange.
Remarque: Si les points n’était pas deux à deux disjoints, les diagonales pourraient tout simplement ne pas exister, et
cet exercice n’aurait plus de sens !
1. Faire une figure.
2. Quelle est l’affixe du milieu de [OB] ? Et de [AC] ? Ainsi, par hypothèse, ces deux nombres sont égaux.
3. Traduire le fait que −−→ OB ⊥−−→ AC.
4. En déduire que ¯ bc +b¯c=¯ ba +b¯a.
5. Achever de montrer que OABC est un losange.
2 Les diagonales d’un losange se coupent à angle droit et en leur milieu
Le but de cette partie est de démontrer que les diagonales d’un losange se coupent à angle droit et en leur milieu.
Nous prendrons encore un losange dont un des sommets est l’origine du repère. Nous fixons donc A,B,Ctrois
points tels que OABC est un losange. Pour simplifier encore, nous supposons que la longueur des côtés de OABC est
1.
Nous noterons comme dans la partie précédente a,b,cles affixes des points A,B,Crespectivement.
2.1 Les diagonales sont orthogonales
1. Que valent |a|et |c|?
2. À partir des hypothèses AB =1 et BC =1, démontrer :
|b|2=a¯ b+¯ab =b¯c+¯ bc
3. Montrer que les diagonales du losange sont orthogonales.
1

2.2 *** Un losange est un parallélogramme
Nous allons maintenant prouver que OABC est un parallélogramme. On pose :
•αun argument de l’affixe de −−→ OA ;
•γun argument de l’affixe de −−→ OC ;
•θun argument de l’affixe de −−→ AB ;
•φun argument de l’affixe de −−→ CB.
Cette partie est plus difficile. On s’y permettra pour simplifier les calculs l’usage de la notation modulo : on rappelle
qu’étant donnés (a,b,m)∈R3, la notation "a≡b[m]" signifie ∃k∈Ztq a=b+km.
1. (division par deux dans un modulo : ) Soit (a,b,m)∈R3. Vérifier :
a≡b[m]⇔(a≡b[2m] ou a≡m+b[2m]).
2. Quelles sont les affixes des quatre vecteurs −−→ OA,−−→ OC,−−→ AB et −−→ CB ?
3. En écrivant l’affixe de Bde deux manières différentes, montrer :
eiα+γ
2sin(α−γ
2)=eiφ+θ
2sin(φ−θ
2).
4. En déduire que :
α−γ≡φ−θ[2π] ou α−γ≡θ−φ[2π]
5. Montrer également que :
α+γ≡φ+θ[2π]
6. Montrer que les situations suivantes sont impossibles :
(a) α≡π+θ[2π] ;
(b) γ≡π+φ[2π] ; (c)
α≡θ[2π]
γ≡φ[2π]; (d)
α=π+φ[2π]
θ=π+γ[2π].
indication: Revenir à l’interprétation géométrique de ces nombres. La contradiction recherchée sera que les
points O,A,B,Cne sont pas deux à deux distincts. Faire des dessins !
7. Finalement, démontrer que −−→ OA =−−→ CB et −−→ OC =−−→ AB, autrement dit que OABC est un parallélogramme.
2.3 Les diagonales se coupent en leur milieu
1. Exprimer ben fonction de aet c. On pourra utiliser le résultat de 2.2.
2. Montrer que le milieu de [OB] est égal au milieu de [AC]. indication: Calculer l’affixe du milieu de [OB], du
milieu de [AC] et vérifier que ce sont les mêmes.
On a bien prouvé que les diagonales du losange OABC se coupent à angles droits et en leur milieu.
3 Une équation dans le cercle trigonométrique
Ici, le but est de déterminer les nombres complexes a,b,cde module 1 tels que a+b+c=1 en utilisant quelques
résultats des parties précédentes.
1. Donner un exemple de nombres a,b,cde module 1 et vérifiant a+b+c=1. Dessiner les points du plan
correspondant.
Dans la suite, on fixe a,b,c trois nombres complexes de module 1 vérifiant a +b+c=1. On définit les points
M,N,P tels que −−→ OM =a, −−−→ MN =b, −−→ NP =c.
2

2. On suppose que les points O,M,N,Psont deux à deux distincts. Démontrer que OMNP est un losange. En
déduire la valeur de b.
3. Dessiner un exemple où les points O,M,N,Pne seraient pas deux à deux distincts.
4. Démontrer que dans tous les cas, un des trois nombres a,b,cvaut 1. Comment sont alors les deux autres
nombres ? Représenter le tout dans le plan. indication: Le cas où les points O,M,N,Pest évident grâce à la
question précédente. Il vous faut donc étudier les cas où deux de ces points seraient égaux. Attention : certains
de ces points ne peuvent pas être égaux.
3