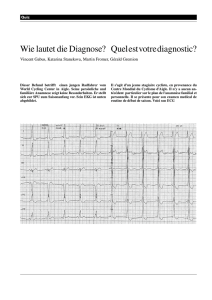
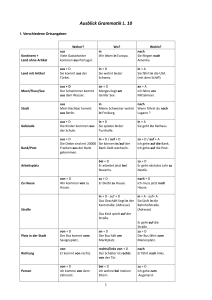
1. Classification des plantes Klassifizierung der Pflanzen 1.1

La phyllotaxie
Phyllotaxis
La phyllotaxie est l’´ etude de la dispostion des ´ el´ ements botaniques (feuilles, graines). C’est ce qui va nous int´ eresser tout au long de cette exposition.
Als Phyllotaxis bezeichnet man die Anordnung der Organe (Bl¨ atter, Bl¨ uten, Samen) einer Pflanze. Sie ist das Thema diser Ausstellung.
1. Classification des plantes Klassifizierung der Pflanzen
1.1 Phyllotaxie distique / Zweizeilige Phyllotaxis
Le b´ egonia est un exemple de phyllotaxie distique. Les feuilles sont ins´ er´ ees
l’une apr` es l’autre et forment un angle de 180◦avec la feuille pr´ ec´ edente.
Ein Beispiel f¨ ur Phyllotaxis bei zweizeiligen Pflanzen ist die Begonie. Die
Bl¨ atter schieben sich – eines nach dem anderen – ein und bilden zum jew-
eilig vorausgehenden Blatt einen Winkel von 180◦.
(a) (b) (c)
Figure 1: (a) et (b) montrent une simulation de l’apparition des 2 premi` eres
feuilles, (c) est un vrai b´ egonia. (a) und (b): Simulationen der Bildung der ersten
beiden Bl¨ atter. (c): eine echte Begonie.)
1.2 Phyllotaxie spiral´ ee / Schraubige Phyllotaxis
L’alo´ e est un exemple de phyllotaxie spiral´ ee. Le principe d’insertion est iden-
tique ` a la phyllotaxie distique, mais l’angle d’insertion n’est pas 180◦, il est
constant et not´ eφ(appel´ eangle de divergence).
Ein Beispiel f¨ ur schraubige Phyllotaxis ist die Aloe. Das Prinzip ist das
gleiche wie bei der zweizeiligen Phyllotaxis, wobei der Winkel hier konstant
ist. Dieser wird mit φbezeichnet und heißt Divergenzwinkel.
(a) (b) (c)
Figure 2: (a) et (b) montrent une simulation de l’apparition des 2 premi` eres
feuilles, (c) est une vraie alo´ e. (a) und (b): Simulationen der Entstehung der ersten
beiden Bl¨ atter. (c): eine echte Aloe
1.3 Phyllotaxie d´ ecuss´ ee / Dekussierte Phyllotaxis
La menthe est un exemple de phyllotaxie d´ ecus´ ee. Deux feuilles oppos´ ees
sont ins´ er´ ees en mˆ eme temps et l’angle de divergence vaut 90◦.
Ein Beispiel f¨ ur dekussierte Phyllotaxis ist die Minze. Gegen¨ uberliegende
Bl¨ atter erscheinen gleichzeitig. Der Divergenzwinkel betr ¨ agt hier 90◦.
(a) (b) (c)
Figure 3: (a) et (b) montrent une simulation de l’apparition des 2 premiers groupes
de feuilles, (c) est une vraie menthe. (a) und (b): Simulation der ersten beiden
Blattgruppen. c: eine echte Minze.
1.4 Phyllotaxie verticill´ ee / Quirlst¨ andige Phyllotaxis
Un mutant du cannabis est un exemple de phyllotaxie verticill´ ee. Plusieurs
feuilles sont ins´ er´ ees en mˆ eme temps (ici 3), l’angle de divergence entre les
groupes de feuilles est constant (120◦).
Eine mutierte Cannabis-Pflanze ist ein Beispiel f¨ ur quirlst¨ andige Phyllotaxis.
Gleichzeitig treten mehrere Bl ¨ atter auf (hier: 3). Der Divergenzwinkel inner-
halb dieser Blattgruppen ist konstant (120◦).
(a) (b) (c)
Figure 4: (a) et (b) montrent une simulation de l’apparition des 2 premiers groupes
de feuilles, (c) est un vrai mutant de cannabis. (a) und (b) : Simulation der ersten
beiden Blattgruppen. (c): Eine echte mutierte Cannabis-Pflanze.
2. Phyllotaxie spiral´ ee Schraubige Phyllotaxis
Dans une plante spiral´ ee, on appelle parastiches les spirales apparentes
form´ ees par les feuilles adjacentes.
In schraubigen Pflanzen werden die sichtbaren Spiralen durch die benach-
barten Bl¨ atter gebildet. Diese nennt man Parastichen.
( a ) Simulation ( b ) ( c )
Figure 5: Sur cette simulation, on compte 8 parastiches droites (b) et 13
parastiches gauches (c). In dieser Simulation, hat es 8 rechte Parastichen (b) und 13
linke Parasitchen (c).
(a) (b) (c)
Figure 6: Sur l’Aeonium Haworthii, on compte 3 parastiches droites (b) et 2
parastiches gauches (c). In der Aeonium Haworthii erkennt man drei rechte
Parastichen (b) und 2 linke Parastichen (c).
Dans la nature, 94% des plantes spiral´ ees ont la particularit´ e que les nombres
de parastiches sont deux nombres de Fibonacci cons´ ecutifs et l’on remarque
que l’angle de divergence φvaut 137.5◦, cet angle est sp´ ecial, on l’appelle
angle d’or.
In der Natur zeigen 94% der schraubigen Pflanzen die Besonderheit, dass die
Anzahl der Parastichen 2 aufeinanderfolgende Fibonacci-Zahlen sind. Der
Divergenzwinkel betr ¨ agt hier 137.5◦. Diesen speziellen Winkel nennt man
Goldenen Winkel.
Suite de Fibonacci, Fibonacci-Folge :
11235813213455. . .
Voici d’autres exemples, Das sind andere Beispiele :
( a ) Mammilaria Perbella ( b ) Tournesol,
Sonnenblume ( c ) Havothia Rigida
Exposition ”Plantes, spirales et nombres”, Jardin botanique, Fribourg, septembre 2010 / Ausstellung ”Pflanzen, Muster und Zahlen”, Botanischer Garten, Freiburg, September 2010