Chapitre 10 : Parallélogrammes particuliers

Chapitre 10 : Parallélogrammes particuliers
I- Les losanges
1) Définition
Définition 1 :
Un losange est un quadrilatère non croisé dont les quatre côtés sont de même
longueur.
2) Propriétés
Propriété 1 :
Un losange est un parallélogramme particulier. Il possède donc toutes les propriétés des parallélogrammes.
Propriétés 2 :
- Un losange possède deux axes de symétrie : ses diagonales.
- Un losange possède un centre de symétrie : le point d’intersection de ses
diagonales.
Exemple :
Pour le losange RING les droites (RN) et (IG) sont ses axes de symétrie, et le point K est le
centre du losange, c’est son centre de symétrie.
Propriété 3 :
Les diagonales d’un losange sont perpendiculaires.
3) Reconnaître un losange
Propriété 4 :
Si un parallélogramme possède deux côtés consécutifs de même longueur, alors c’est un losange.
Exemple :
Dans le parallélogramme LOSA on a LO = OS, donc LOSA est un losange.
Propriété 5 :
Si un parallélogramme possède des diagonales perpendiculaires, alors c’est un losange.
Exemple :
FIER est un parallélogramme et ses diagonales (FE) et (IR) sont
perpendiculaires.
Donc FIER est un losange.
II- Les rectangles
1) Définition
Définition 2 :
Un rectangle est un quadrilatère dont les quatre angles sont droits.
2) Propriétés
Propriété 6 :
Un rectangle est un parallélogramme particulier. Il possède donc toutes les propriétés des parallélogrammes.

Propriétés 7 :
- Un rectangle possède deux axes de symétrie : les médiatrices de ses
côtés.
- Un rectangle possède un centre de symétrie : le point d’intersection de
ses diagonales.
Exemple :
Pour le rectangle EFGH les droites d et d’ sont ses axes de symétrie, et le point K
est le centre du rectangle, c’est son centre de symétrie.
Propriété 8 :
Les diagonales d’un rectangle sont de même longueur.
3) Reconnaître un rectangle
Propriété 9 :
Si un quadrilatère possède trois angles droits, alors c’est un rectangle.
Exemple :
Dans le quadrilatère ABCD les angles 𝐷𝐴𝐵
, 𝐴𝐵𝐶 et 𝐵𝐶𝐷 sont droits donc ABCD est un
rectangle.
Propriété 10 :
Si un parallélogramme possède un angle droit, alors c’est un rectangle.
Exemple :
Dans le parallélogramme RECT l’angle 𝐸𝐶𝑇
est droit donc RECT est un rectangle.
Propriété 11 :
Si un parallélogramme possède des diagonales de même longueur, alors c’est un rectangle.
Exemple :
Dans le parallélogramme DOUB les diagonales [DU] et [OB] sont de même longueur.
Donc DOUB est un rectangle.
III- Les carrés
1) Définition
Définition 3 :
Un carré est un quadrilatère dont les quatre angles sont droits et dont les quatre côtés sont
de même longueur.
2) Propriétés
Propriété 12 :
Un carré est donc un losange particulier et un rectangle particulier. Il possède donc toutes les propriétés des
losanges et des rectangles.
Remarque :
Un carré est donc un parallélogramme particulier.
Propriétés 13 :
- Un carré possède quatre axes de symétrie : ses diagonales et les
médiatrices de ses côtés.

- Un carré possède un centre de symétrie : le point d’intersection de ses diagonales.
Exemple :
Pour le carré AVEC les droites d, d’, (AE) et (CV) sont ses axes de symétrie, et le point I est le centre du carré, c’est
son centre de symétrie.
Propriété 14 :
Les diagonales d’un carré sont de même longueur et sont perpendiculaires.
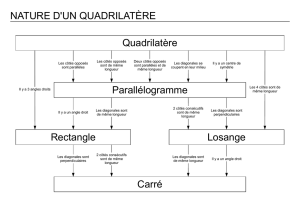
IV- Récapitulatif
Quadrilatère
(non croisé)
Rectangle
3 angles droits
ou
Les diagonales se coupent en leur
milieu et sont de même longueur.
Les côtés opposés parallèles 2 à 2
ou
Les côtés opposés de même
longueur
ou
Les diagonales se coupent en leur
milieu
ou
2 côtés de même longueur et
parallèles
Parallélogramme
Carré
1 angle droit
ou
Les diagonales de
même longueur.
2 côtés consécutifs de
même longueur
ou
Les diagonales
perpendiculaires
Losange
4 côtés de même longueur
ou
Les diagonales se coupent
perpendiculairement en
leur milieu
1 angle droit
ou
Les diagonales de
même longueur.
2 côtés consécutifs de
même longueur
ou
Les diagonales
perpendiculaires