Partie I : La réflexion totale Partie II : Application médicale – La

Thème : Santé
Chap. : Ondes lumineuses
TP : Le miroir subaquatique.
2nde
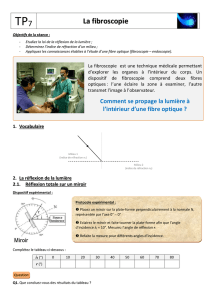
But du TP : Etudier la réfraction et ses applications.
Partie I : La réflexion totale
Avez-vous déjà remarqué que parfois, lorsqu’on est
sous l’eau, on peut voir sa réflexion sur la surface ?
Comment expliquer ce phénomène ? C’est ce que nous
allons découvrir aujourd’hui.
1. Nommer les différents rayons du schéma ci-contre, ainsi que les 3 angles i, i’ et r.
Protocole expérimental :
 Placer le demi-disque de plexiglas et tourner sa face convexe (non plane) vers la lanterne.
 Superposer le faisceau incident, issu de la lanterne, avec la perpendiculaire à la face plane, la normale.
L’angle d’incidence lu doit être égal à 0° (i = 0°) et le point d’incidence I doit être au centre du disque.
Le faisceau ne doit pas être dévié dans cette configuration, si ce n’est pas le cas, régler le faisceau grâce
aux vis sur les côtés de la lanterne.
 Faire pivoter le disque pour obtenir les différentes valeurs de l’angle d’incidence i. On peut alors lire la
valeur de l’angle de réflexion i’ et de réfraction r.
Ces angles auront des valeurs entre 0 et 90.
2. Compléter le tableau de l’annexe 1 (avec 2 décimales pour les sinus). Si l’angle n’existe pas, utiliser un
tiret « - ».
Attention votre calculatrice doit être en mode degrés pour calculer le sinus des angles donnés en degrés
3. A partir d’un certain angle limite i=ilim, on remarque un phénomène particulier. Qu’observe-t-on ?
Donner un encadrement (entre tel angle et tel angle) de la valeur de ilim.
4. Observait-on le même phénomène au dernier TP ? Qu’a-t-on changé entre ce protocole expérimental et
celui de l’étude de la réfraction du dernier TP ? Exprimer votre réponse en comparant les indices de réfraction
des milieux.
Donées : nair = 1,00 ; nverre = 1,50 (le plexiglass est un verre organique)
5. Placez le faisceau à l’angle d’incidence limite ilim. Noter la valeur mesurée de ilim. Quelle est alors la valeur
de l’angle de réfraction rlim ?
6. Pour i>ilim, les phénomènes de réflexion ET de réfraction sont-ils toujours observés ?
7. Retrouver ilim par le calcul, en utilisant la valeur de rlim trouvée précédemment ainsi que la loi de la
réfraction de Descartes. Comparer ce résultat à l’angle d’incidence limite que vous avez mesuré.
8. Conclusion : Quelles sont les DEUX conditions pour observer le phénomène de réflexion totale ?
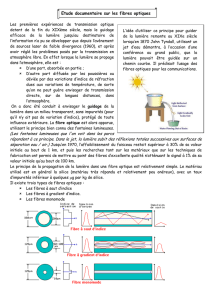
Partie II : Application médicale – La fibroscopie
La fibroscopie est un examen médical utilisant des fibres optiques pour canaliser la lumière.
Document 1 : La fibre optique
La fibre optique est constitué d’un cylindre de verre de diamètre égal à 10 µm appelé
cœur. Ce cœur est recouvert d’une gaine transparente. La fibre optique est utilisée pour
de multiples applications : en télécommunications pour assurer le transport de données
très rapide (internet…) ou encore en médecine pour la fibroscopie.
Dans un fibroscope, une partie des fibres optiques transporte la lumière vers l’organe à
observer tandis que d’autres fibres optiques assurent le transport de l’image de l’organe
vers le médecin pour qu’il puisse examiner la zone.

Document 2 : Images de fibres optiques
Document 3 : La fibroscopie
La fibroscopie est un examen qui
consiste à introduire dans le corps du
patient un tube souple très fin sous
anesthésie locale voire générale. Ce tube
contient des fibres optiques et une
caméra. Cela permet ainsi l’observation
des organes du corps humain : poumons, organes du système
digestif, cordes vocales, …
9. Dans la fibre optique, où sort le rayon lumineux ? Quel phénomène optique est donc utilisé dans la fibre
optique pour canaliser les rayons lumineux (qui se réfléchissent sur des milieux transparents) ?
10. Que peut-on en déduire de l’indice de réfraction de la gaine par rapport à celui du cœur ?
11. Compléter le schéma de l’annexe 2 avec les rayons lumineux en montrant comment la fibre canalise la
lumière en utilisant de multiples réflexions totales.
12. Combien faut-il de fibres optiques pour réaliser une fibroscopie ? Pourquoi ?

Annexes
Annexe 1
i (°)
0
10
20
30
40
50
60
70
80
r (°)
Sin(i)
Sin(r)
Annexe 2
Annexes
Annexe 1
i (°)
0
10
20
30
40
50
60
70
80
r (°)
Sin(i)
Sin(r)
Annexe 2