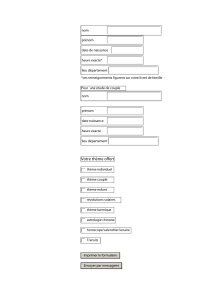
Suite exacte à six termes en K-théorie pour les produits

K
C∗
Z

1980
K
C∗Z
C∗
K
C∗
C∗
C∗

C∗A A+C∗
A+={(a, λ)∈A×C}
(a, λ)(b, µ)=(ab +λb +µa, λµ)
(a, λ)∗= (a∗, λ)
||(a, λ)|| = sup{||ax +λx|| :x∈A, ||x|| = 1}.
0A A+C0
πC.
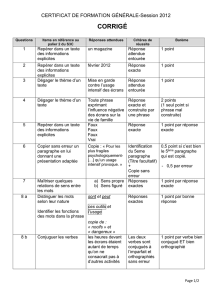
S GS
S µ :S→GS
G α :S→G
˜α:GS→G α =µ◦˜α
S G
GS
α
∃!˜αµ
GSS×S
(x, y)∼(x0, y0)∃r∈S/x +y0+r=x0+y+r.
S×S/ ∼(x, x)
x∈S(x, y)
(y, x) [x]−[y] (x, y)
C∗
{φij :Aj→Ai}i>j i j
φij ◦φjk =φik i > j > k.
A∞
{Ai;φij }φi:Ai→A∞
AiA∞
Aj
φi
φj
φij

A∞=∪φj(Aj)
A0
∞φ0
i:Ai→A0
∞
A∞→A0
∞
AiA∞
AjA0
∞
φi
φ0
i
φij
φj
φ0
j
φ0
j
A∞=∪φ0
jAj
x=φj(aj)
α(x) := sup
i{||φij (aj)||}
C∗A∞
α
C∗
C∗AΓ
Γ
α:γ→(A)αs
α s (A, Γ, α)
C∗(π, U)π∗
A H s 7→ UsΓ
C∗(A, Γ, α)
Usπ(a)U∗
s=π(αs(a)) ,∀a∈A, s ∈Γ.
Γ
AΓA[Γ]
f=X
s∈Γ
ass,
sas−1=α(a),∀a∈A, s ∈Γ.
(as)∗=s−1a∗
f, g ∈A[Γ]
fg =X
s X t
fst−1πst−1(gt)!s,

f∗=X
s
πs(f∗
s−1)s.
(π, U) (A, Γ, α)∗
A[Γ]
˜π(f) = X
s∈Γ
π(fs)Us.
∗˜π A[Γ]
π(a) = ˜π(a1Γ)Us= ˜π(1As)A
uλA Us= limλ→∞ ˜π(uλs)
AΓC∗
A[Γ] ∗
||f|| = sup
˜π||˜π(f)||
˜π∗A[Γ]
Ps||fs||
∗A[Γ] sup
∗A
H∗A[Γ]
Γ
l2(G, H) = {x:G→H:X||xs||2<∞},
(A, Γ, α)
(π0(a)x)s=π(αs(a))xs,
(Λtx)s=x(t−1s).
A×αΓ
sup
AΓ Γ
Z
(π, U) (A, Γ, α)∗
A×αΓC∗π(A)U(Γ)
˜π(f) = X
s
π(fs)Us