Problème 1. Pavage d`un échiquier à défaut par des triominos

Problème 1. Pavage d’un échiquier à défaut par des triominos
(i) On considère un échiquier comportant 2n × 2n carrés où n = 1, 2, 3, .... (voir fig 1 pour n = 1, 2, 3).
Maintenant nous supposerons qu’il y a un carré manquant quelque part (cf fig2). Un tel échiquier sera appelé échiquier à défaut.
La question : Est-ce qu’un échiquier à défaut peut être recouvert par des triominos (cf fig 3) en forme de L ?
Les triominos peuvent être tournés dans tous les sens. La figure 4 est un exemple où le carré manquant est en bas à gauche.
Le but : Prouver que le pavage d’un échiquier à défaut de dimension 2n × 2n par des triominos en forme de L est possible pour tout n ≥ 1.
Calculer combien de triominos en forme de L sont nécessaires.
(ii) Considérons le même problème mais avec un échiquier de m × n (m, n sont des entiers naturels)
Question: pour quelles valeurs de m et de n le pavage d’un échiquier à défaut avec des triominos en forme de L est-il possible ?
(difficile)
(iii) Considérons un échiquier T(n), constitué de triangles équilatéraux de côté 1 et comportant 2n triangles de chaque côté. Un
triomino triangulaire est une pièce faite de trois triangles (cf figure ci-dessous).
Etudiez la possibilité de recouvrir un tel échiquier à défaut pour lequel un triangle dans un coin est manquant.
Faites la même chose pour un échiquier à défaut constitué de triangles équilatéraux de côté 1 et comportant m triangles de chaque côté
où m est un entier naturel.

Problème 2. La suite des nombres de Fibonacci
La suite des nombres de Fibonacci est 1, 1, 2, 3, 5, 8, 13, ... où chaque nombre est la somme des deux
précédents. Cette suite de nombres possède de nombreuses propriétés qui ne sont pas seulement des curiosités
mathématiques : la suite des nombres de Fibonacci joue un rôle important dans de nombreuses applications et
aussi dans la résolution du célèbre problème numéro 10 de Hilbert, la résolubilité des équations diophantiennes.
Posons F1 = F2 = 1, alors le nème nombre de la suite peut être obtenu ainsi :
(1) Fn = Fn−1 + Fn−2 pour n ≥ 3.
Le problème que nous voulons étudier est la relation algébrique entre la suite de Fibonacci et la divisibilité
(i) Etudiez le reste des nombres de Fibonacci dans la division euclidienne par N où N = Fn (n ≥ 3). Quand est ce
que le reste est 0 ?
Exemple : si nous choisissons N = 3 = F4 alors les restes de F1, F2, ... sont 1, 1, 2, 0, 2, 2, 1, 0, 1, 1, 2, 0, ...
Conclusion: Fm est divisible par Fn noté Fn|Fm lorsque m est divisible par n, i.e. n|m. (m est un entier naturel). Prouvez cette propriété.
De cette conclusion nous voyons que Fpgcd(m,n)|Fm and Fpgcd(m,n)|Fn. Ainsi il est vrai que pgcd(m,n)|pgcd(Fm, Fn).
(ii) Nous pouvons prouver encore plus :
Théorème : Fpgcd(m,n) = pgcd(Fm, Fn) où m, n ≥ 1.
En prouvant les lemmes
Lemme 1 : Il existe des entiers a et b tels que pgcd(m, n) = am + bn.
Lemme 2 : Fm+n = Fm−1Fn + FmFn+1, Fm−n = (−1)n+1(Fm−1Fn − FmFn−1).
(iii) A partir de (ii) nous pouvons prouver les conséquences suivantes :
(a) Fn et Fn+1 n’ont aucun diviseur commun (n ≥ 1).
(b) Fm|Fn si et seulement si m|n (m, n ≥ 1).
(iv) Nous pouvons aussi prouver les identités suivantes :
Fn+1
2= FnFn+2 + (−1)n
F1
2 + F2 2 + · · · + Fn 2 = FnFn+1
F1F2 + F2F3 + · · · + F2nF2n+1 = F2n
2
Fn
2 + Fn+1 2 = F2n+1
F1 + 2F2 + 3F3 + · · · + nFn = nFn+2 − Fn+3 + 2
(iv) Retrouver la suite des nombres de Fibonacci dans le célèbre triangle de Pascal :

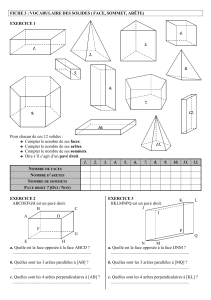
Problème 3. Polygones et polyèdres
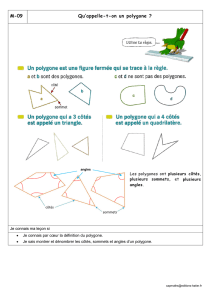
Un polygone est une figure fermée délimitée par des segments. Les segments sont appelé arêtes du polygone, et leur point d’intersections
les sommets. Un polygone a le même nombre de sommets et d’arêtes. Ainsi, si le nombre d’arêtes est A et le nombre de sommets S alors
A – S = 0
Si toutes les arêtes ont la même longueur et si tous les angles ont la même mesure alors le polygone est dit régulier. Un polygone à n-côtés
est appelé n-gone. Un 3-gone régulier est un triangle équilatéral, un 4-gone régulier un carré, etc.
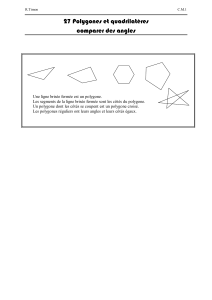
Exemples de polygones réguliers :
Les polygones irréguliers ont des arêtes de différentes longueur et des angles de différente mesure. Si un polygone n’a pas toutes ses
arêtes de même longueur et tous ses angles de même mesure alors le polygone est dit irrégulier.
Exemples de polygones réguliers :
(i) Déterminer la mesure d’un angle d’un triangle, d’un carré, d’un pentagone puis d’un n-gone.
(ii) Déterminer la mesure de l’angle entre chaque arête d’un n-gone.
Les polygones au-dessus sont tous convexes.
Un polygone du plan est dit convexe s’il contient tous les segments reliant deux de ses points quelconques.
Un polygone concave est un polygone qui n’est pas convexe. Un polygone est concave si au moins un de ses angles internes a une mesure
plus grande que 180 degré.
Un polyèdre est une figure de l’espace délimitée par des polygones. Nous supposerons désormais que les polygones sont convexes. Les
surfaces planes constituées de polygones sont appelées faces, les intersections des faces sont appelées arêtes et l’intersection des arêtes
sont appelées sommets.
Il y a au moins 4 sommets dans un polyèdre. Un polyèdre à quatre sommets possède 6 arêtes et 4 faces et se nomme tétraèdre.
Soit F le nombre de faces, A le nombre d’arêtes et S le nombre de sommets. Existe-t-il une relation entre ces trois nombres ?
(iii) Montrer que cette égalité (appelé relation d’Euler) est vraie pour tous les polyèdres.
Un polyèdre est dit régulier (ou solide de Platon) si toutes les faces, les arêtes et les sommets sont « identiques. Un polyèdre régulier a
ainsi des n-gones réguliers pour faces, des arêtes de même longueur et des angles entre les arêtes de même mesure.
(iv) Montrer qu’un polyèdre régulier possède soit des triangles, soit des carrés ou soit des pentagones réguliers comme faces.

Supposons désormais que r faces se rencontrent à chaque sommet et chaque face soit un n-gone.
(v) Montrer que (r − 2)(n − 2) < 4.
(vi) Montrer que les seules solutions de cette inégalité sont (r, n) = (3, 3),(3, 4),(3, 5), (4, 3) et (5, 3).
Il ne peut y avoir qu’une seule figure pour chaque solution car la forme autour d’un sommet détermine toute la figure (sauf la taille). Pour
chaque solution nous pouvons construire un polyèdre régulier, et nous obtenons le tétraèdre, l’octaèdre, l’icosaèdre, le cube, le
dodécaèdre. Le nombre des faces est respectivement 4, 8, 20, 3, et 12.
Soit K un polyèdre régulier. Nous construisons un nouveau polyèdre K’ en prenant pour sommet le centre de chaque face de K et en
prenant pour arêtes les segments reliant deux points issus de deux faces adjacentes. Le nouveau polyèdre K’ est appelé le dual de K et c’est
aussi un polyèdre régulier.
(vii) Déterminer le dual de chacun des cinq polyèdres réguliers.
(viii) Reproduisez les figures ci-dessous et construisez les cinq polyèdres réguliers.

Problème 4. Est-ce qu’un beignet et une tasse de café sont la même chose ?
(i) Prenez un beignet que l’on supposera indéfiniment extensible. Etirez-le jusqu’à obtenir une tasse de café,
puis revenez à sa forme initiale. Vous pouvez étirer, plier, mais vous n’avez pas le droit de détruire le trou
qui est déjà là. Pouvez-vous expliquer comment cela est possible ?
En mathématiques de telles déformations sont appelées homéomorphismes.
Vous pourrez ainsi dire à votre grand-mère que les mathématiciens ne font aucune différence entre une
tasse de café et un beignet. Vous pouvez aussi servir à votre père un beignet s’il demande une tasse de café
et vice versa.
(ii) Prenez une feuille de papier. Pouvez-vous faire beignet ? (que nous appellerons tore) Dessinez un tore
sur une feuille de papier.
Notez que nous avons construit un tore à partir d’une feuille de papier. Ce tore n’est pas plat, il est courbé
d’une manière non constante.
Ce tore « réel » a la même topologie que le tore construit en papier. Cependant il n’est pas courbé
et n’a pas besoin de trois dimensions pour exister. Nous pouvons nous débarrasser de cette
troisième dimension et visualiser une surface compacte en utilisant une surface pavée.
Pourriez-vous m’aider à faire cela ?
Nous pourrions essayer de paver un espace plan avec des formes élémentaires mais nos efforts ne
seraient pas récompensés (rappelez.-vous, nous parlons de formes identiques ; les rotations sont
interdites donc les triangles ne vont pas convenir !)
Par exemple, essayez de paver une surface plane avec des octogones. Quelle est la mesure des
angles intérieurs d’un octogone ? Peut-on paver le plan avec des octogones ?
Que pourriez-vous donc dire à votre mère si elle veut des carreaux octogonaux pour sa salle de bain ?
Quelles sont les formes qui peuvent paver une surface plane ?
(iii) Coupez une bande de papier. Faites tourner d’un demi-tour un des côtés, puis reliez les extrémités de la bande de papier ensemble
pour former un ruban. Etudiez combien de côtés vous obtenez.
Imaginez une fourmi rampant sur le ruban. Peut-elle rejoindre son point de
départ sans quitter le ruban ? Vous pouvez utiliser un stylo à la place d’une
fourmi 
Un tel ruban est appelé ruban de Möbius.
Maintenant coupez le ruban en son milieu (selon le chemin de la fourmi).
Qu’observez-vous ?
Que se passe t’il si vous faites un tour complet avant de coller le ruban ?
Un tour et demi ? Deux ? etc.
Essayez de tirer une conclusion de ces expériences.
(iv) Savez-vous si les mathématiciens peuvent distinguer une tasse de café
d’un ruban de Möbius ? Expliquez votre supposition.
(v) En collant la partie supérieur d’un ruban de Möbius à sa partie inférieure,
on obtient une bouteille de Klein, une forme compliquée. Il est possible de la représenter correctement en trois dimensions. Essayez d’en
représenter une.