Devoir de spécialité

Devoir de spécialité
Extraits de la notice d'utilisation d'un télescope
Caractéristiques :
Télescope 114/900 de type
Référence: T41
Télescope Newton à miroir alumine, sur monture équatoriale pour toutes observations : lunaires,
planétaires, stellaires.
Diamètre: 114 mm
Focale: 900 mm
Oculaires: 6 mm, 9 mm, 12 mm et 20 mm
Grossissements : 45×, 75×, 100× et 150×.
Monture équatoriale avec flexibles, motorisable, trépied aluminium.
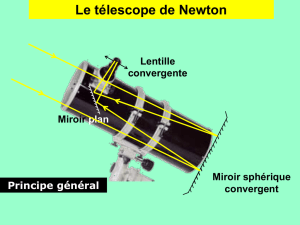
Le télescope est un système optique conçu pour l'observation des astres. Le télescope que vous avez acheté
s'appelle un télescope réflecteur type Newton. C'est un tube ouvert à une extrémité avec un miroir courbe à
l'autre.
Les rayons lumineux rentrent par l'extrémité ouverte du tube et viennent frapper le miroir courbe appelé "miroir
principal".
Les rayons réfléchis par ce miroir viennent ensuite en frapper un second appelé " miroir diagonal" (miroir
secondaire) situé à 80cm du miroir principal.
Ce petit miroir plan, placé au centre du tube à 45 degrés, renvoie l'image formée par le miroir principal, sur le
côté où on l'observe avec l'oculaire qui joue le rôle de loupe.
Par suite de la courbure du miroir principal, les rayons de lumière sont courbés pour se concentrer en un point.
Le miroir principal d'un télescope doit être poli exactement selon la courbure appropriée afin de garantir le
point focal correct. Il est très important que les deux miroirs soient dans le bon alignement pour obtenir les
meilleurs résultats. (A vérifier régulièrement).
Ce télescope est muni d'une monture équatoriale qui permet le déplacement du tube et donc l'observation d'un
astre dans toutes les directions.
Partie A : Questions sur la notice
1. Que signifient les indications: Diamètre 114 mm, Focale 900 mm ?
2. Quel est le nom de la grandeur dont on donne la valeur en mm avec chaque oculaire ?
3. Dans la phrase suivante "Par suite de la courbure du miroir principal, les rayons de lumière sont courbés
pour se concentrer en un point".
a) Que représente ce point pour le miroir principal ?
b) Le mot « courbés » employé à propos des rayons lumineux est impropre. Expliquer ce que veut dire
l'auteur de la notice en l'utilisant.
Partie B : Analyse du fonctionnement : observation d'un astre.
Modélisation du télescope de Newton:
Dans tout l'exercice, nous modéliserons :
•le miroir principal par un miroir sphérique de sommet S et de foyer F'1
•l'oculaire par une lentille mince convergente de centre optique O2 et de focale f'2 et dont l'axe optique est
perpendiculaire à celui du miroir principal ;
•le miroir secondaire par un miroir plan dont le milieu M est placé sur l'axe optique du miroir principal et
sur l'axe optique de l'oculaire.
1.
Formation des images
Le télescope est pointé vers un astre avec l'oculaire de 20 mm. On assimilera l'astre à un objet (AB), situé à
l'infini et vu sous l'angle apparent θ, le point A étant situé sur l'axe du miroir principal.
Le miroir principal donne de l'objet (AB) une image (A1B1).
a) Dans le télescope "114/900", quelle est la valeur de la distance A1S ? Justifier brièvement.
b) (A1B1) joue le rôle d'objet pour le miroir secondaire qui en donne une image (A2B2)
Construire sur un schéma, sans échelle particulière, avec SM = 15 cm, MA1 = 3cm, et pour y voir quelque
chose O2F2 = 2cm , avec ce qui est indiqué ci-dessus, et avec l'image (A2B2). Justifier brièvement.
(A2B2) est examinée à travers l'oculaire qui en donne une image définitive (A'B') à l'infini.
S
M
O2
rayons lumineux issus de B situé à l'infini
B1
A1
α

c) Placer les foyers image F'2 et objet F2 de l'oculaire pour que l'image définitive soit rejetée à l'infini.
d) Construire deux rayons émergents de l'oculaire et issus de B2.
e) Construire, à travers la totalité de l'instrument, la marche du faisceau lumineux issu de B et limité par les
deux rayons incidents fléchés.
2. Grossissement
L'observateur qui regarde dans le télescope voit l'image définitive sous l'angle θ'. On définit le grossissement
dans le cas d'une vision à l'infini
G=θ '
θ
; θ' et θ sont exprimés en radian.
a) Établir que G est aussi égal au quotient de la distance focale du miroir principal par celle de l'oculaire. (Les
angles sont petits : sin θ = tan θ = θ (en rad)).
b) Quel oculaire doit-on choisir pour que le grossissement soit 150x ?
Partie C : Observation du Soleil.
Le Soleil est une étoile située à 149 597 870 km de la Terre dont le diamètre moyen est de 1 392 000 km. Il est très
dangereux d'observer directement le Soleil à travers l'oculaire : l'intensité lumineuse peut endommager
définitivement la rétine de l'œil.
Pour observer le soleil on place un écran à 50 cm derrière l'oculaire (on considérera cette distance comme
constante). On observe alors l'image du soleil sur l'écran, les tâches solaires étant parfaitement visibles.
1. Calculer la position de l'oculaire : comment placer les foyers image F'2 et objet F2 par rapport à A2B2 pour
que l'image définitive soit nette sur l'écran.
2. Calculer l'angle θ correspondant à l'angle sous lequel on voit le Soleil à l'oeil nu depuis la Terre.
3. Si on utilise l'oculaire de 12mm, calculer la taille de l'image du soleil sur l'écran.
Partie D : Comparaison de résolutions de deux télescopes.
Le télescope du mont Palomar (à 1800 m d'altitude aux États-Unis) est de type Newton: la lumière réfléchie par
le miroir principal est ensuite réfléchie par un petit miroir secondaire. Le miroir principal est parabolique mais
nous ferons l'approximation qu'il s'agit d'un miroir sphérique, de diamètre D = 5,08 m, de distance focale
f = 16,3 m. Le miroir secondaire est plan et situé à d = 14 m du sommet du miroir principal, et incliné à 45° sur
l'axe optique de celui-ci.
On veut observer à l'aide d'une lentille oculaire de distance focale f ' = 0,50 m.
Une qualité recherchée pour un instrument d'optique est sa capacité à discerner deux détails voisins, par
exemple, séparer une étoile double, voir un cratère lunaire de petite dimension ou encore des détails planétaires
subtils.
Les lois de l'optique géométrique font que deux points distincts A et B donnent deux images séparées. Mais
différents phénomènes (dont la diffraction des ondes) entraînent que l'observateur O ne peut discerner deux
images distinctes que si l'angle
AOB
est supérieur à l'angle (x appelé limite de résolution.
A et B donnent pour l'observateur placé en O deux images distinctes.
Schéma
On montre que, pour des points à l'infini et un instrument dont le diamètre de l'objectif est D, la limite de
résolution, exprimée en radians, pour une lumière de longueur d'onde lambda (en mètres) vaut
α=1,22×λ
D
;.
a) Calculer la limite de résolution α1 du télescope « 115/900 » étudié précédemment pour une longueur d'onde
de 500 nm.
b) Calculer la limite de résolution α2 du télescope du mont Palomar pour la même longueur d'onde.
c) On observe la Lune, située à 384400 km de la surface de la Terre. Calculer la distance entre deux points que
l'on peut distinguer sur la Lune avec le « 115/900 » et avec le télescope du mont Palomar (cela correspond à
la taille du plus petit détail que l'on puisse distinguer).
α
O
A
B