Formation des PLC2 de mathématiques Année 2008-2009

Formation des PLC2 de mathématiques
Année 2008-2009
Séminaire de didactique des mathématiques
Î Séance 6 : jeudi 12 mars 2009
[PLC2Maths0809_Seminaire6]
0. Le bulletin officiel .................................................................................................................. 1
1. Questions de la semaine ......................................................................................................... 1
2. Forum des questions ............................................................................................................... 6
3. Exposés ................................................................................................................................. 20
4. Le travail d’étude et de recherche (TER) : l’évaluation ....................................................... 20
L Ce jeudi après-midi, le GSF de Roland Pouget aura lieu sur le site de Rangueil (salle 8), à
partir de 14 h 15.
L En raison des mouvements sociaux, les cours prévus le jeudi 19 mars sont annulés. La
journée du jeudi 26 mars est réorganisée comme suit en quatre séances d’une heure et demie.
Groupe A Groupe B Groupe C
9 h – 10 h 30 Outils didactiques 4 Enseigner la statistique 3 TICE 2
10 h 45 – 12 h 15 TICE 2 Outils didactiques 4 Enseigner la statistique 3
13 h 45 – 15 h 15 Enseigner la statistique 3 TICE 2 Outils didactiques 4
15 h 30 − 17 h GDM
0. Le bulletin officiel
• Abonnement au Bulletin officiel
http://www.education.gouv.fr/cid2560/abonnement.html.
• Bulletin officiel n° 9 du 26 février 2009
Enseignements élémentaire et secondaire / Vie scolaire / Fournitures scolaires.
http://www.education.gouv.fr/cid23891/mene0900080c.html.
1. Questions de la semaine
1.1. La question de la semaine
PLC2Maths0809_Seminaire6 1

Noter la question sur une feuille de format A5, orientation paysage. Indiquer en haut de la
page la semaine, la date, ses prénom et nom ainsi que ses classes en responsabilité et les
initiales de son formateur référent. Merci !
Semaine 23
Jeudi 12 mars 2009
Aurore Dupin (2de et TPE 1re S, GC)
a) Lors du ramassage puis de la correction du dernier DM donné à mes élèves, l’un
d’eux était absent. À son retour, je lui ai demandé de me rendre son DM comprenant les
exercices initialement demandés augmenté d’un exercice supplémentaire de même
difficulté. Mon but était de vérifier que les notions en jeu étaient comprises et de lui
permettre d’avoir une note comme ses camarades. L’élève a pris cela comme une
sanction malgré mes explications. Comment aurais-je pu / dû gérer cette situation ?
b) Dans la construction de mon cours en statistique, je vois qu’il est conseillé un
« résumé numérique par une ou plusieurs mesures de tendance centrale », dont la classe
modale. Et là, surprise ! Dans mon manuel (Transmath 2de), je vois une définition de
la classe modale alors que dans le Déclic 1re ES, la définition est différente. Par
exemple, soit le diagramme suivant :
Dans le Transmath 2de, la classe modale est [a, b], la classe de plus grande aire. Dans
le Déclic 1re ES, la classe modale est [d, e], la classe la plus haute. Qu’en est-il ? Je ne
souhaite pas introduire une notion erronée !
1.2. Les dernières questions de la semaine et quelques « réponses express »
Les questions repérées par un pique bleu (♠) seront abordées dans le forum express. Les
éléments de réponse seront quelquefois apportés uniquement oralement.
Les questions repérées par un trèfle rouge (♣) sont abordées dans le forum des questions.
Î Sur la validation des compétences du C2i2e
http://portfolio.toulouse.iufm.fr
Un document sera prochainement déposé sur le BV qui fournira quelques indications
concernant les dépôts restant à réaliser.
• Comment peut-on savoir quand doit-on valider des compétences pour le portfolio ? Je n’ai pas
compris ce que l’on attend de nous.
♠ Quelle est la date limite pour l’évaluation du C2i2e ?
La date limite, à partir de laquelle il sera impossible aux stagiaires de déposer des documents sur
le portfolio, est fixée au 9 mai 2009. Cela dit, afin de réguler aussi bien le travail des stagiaires
a
b
c
e
d
PLC2Maths0809_Seminaire6 2

que celui des formateurs, une date limite a été fixée pour chacune des compétences. Elles sont
indiquées dans la colonne de droite du tableau des « Productions attendues », situé en bas de la
page de la compétence C8.
• Quel type de document faut-il déposer dans le portfolio ?
• Pourrions-nous avoir une formation ou des indications sur la façon d’intégrer des documents
dans le portfolio et sur la nature des documents à fournir ?
♠ Les documents que nous déposons sur le portfolio peuvent-ils être des documents tirés de stage
réalisés pendant l’année de préparation IUFM au CAPES ?
Non. On n’acceptera pour valider les compétences du C2i2e que des documents réalisés lors de
cette année de stage.
♠ Pour la validation des compétences C31 et C41, je n’ai pas compris quel travail doit être déposé
sur le portfolio.
Pour les compétences (au sens du cahier des charges) autres que la compétence C8 (qui est
validée par le C2i2e), aucun travail ne doit être déposé sur le portfolio. Seul l’un des groupes de
suivi (celui qui est dirigé par Roland Pouget) utilise le portfolio pour l’évaluation desdites
compétences.
♠ Pour la validation du C2i2e, faut-il faire une séance TICE lors de la 2e visite ?
Il n’est pas obligatoire de réaliser une séance utilisant les TICE lors de la 2e visite. C’est par
contre tout à fait possible (et souhaitable) dans le cas où leur utilisation s’avère pertinente.
• Comment utiliser le portfolio ?
• Comment déposer un document à partir de l’ENT ? (Séquence d’enseignement, activités,
devoirs, DS, …)
♠ Est-ce le sujet de bac blanc de terminale ES préparé en équipe au sein du lycée peut être déposé
sur le portfolio pour valider une compétence ?
Il est tout à fait possible d’utiliser un tel document, par exemple pour valider la compétence B12 :
« Contribuer à une production ou à un projet collectif au sein d’équipes disciplinaires,
interdisciplinaires, transversales ou éducatives. » Il faut bien entendu présenter le travail effectué,
mais ce conseil est valable pour tous les documents déposés.
♠ Dans une des compétences du C2i2e à valider, il est demandé un rapport sur la participation à
un projet pluridisciplinaire dans l’établissement. Cela veut-il dire qu’on doit dès à présent faire
partie d’un projet pluridisciplinaire dans notre établissement ? Que se passe-t-il s’il n’y en a pas ?
Cette question fait référence à la compétence B13 : « Concevoir des situations de recherche
d’information dans le cadre des projets transversaux et interdisciplinaires. » Dans le cas où l’on
ne participe pas à un projet pluridisciplinaire dans l’établissement, il est possible d’utiliser des
documents correspondant à des situations de recherche d’information qui auront été proposées à
la classe, du moment que ces situations se réfèrent à plusieurs disciplines (mathématiques &
économie ; mathématiques & histoire ; mathématiques & géographie ; etc.) Il faut alors bien
décrire l’organisation mise en place.
♠ [Par courriel en date du 26/02/2009] Je souhaite déposer sur le portfolio le document visant à
valider la compétence B12. Mon souci est le suivant : dois-je mettre quelque chose en particulier
dans la case « activité du référentiel professionnel » ? Est-ce que cela correspond au descriptif de
l’une ou l’autre des compétences (par exemple C1, C2, C3, ou B1, B12, etc.) ?
Tous ces champs sont en liaison avec des renseignements qui permettront de retrouver les fichiers.
Pour renseigner ce champ, même si c’est redondant, on peut indiquer la ou les compétences visées
par le travail effectué.
PLC2Maths0809_Seminaire6 3

Î Sur le stage de pratique accompagnée
• Pour notre rapport de SPA, pouvons-nous le déposer non signé sur le BV et le renvoyer signé
hors délai (après le 23 février) ?
♠ Le rapport de SPA doit-il être rendu manuscrit ou par mail ?
♠ Faut-il donner le rapport de SPA sous forme papier ou par mail ?
Le rapport de SPA doit être rendu sur support papier et sous forme électronique :
− il faut rendre au secrétariat une version sur support papier, à raison d’un exemplaire par
stagiaire : cet exemplaire figurera dans le dossier de validation ;
− il faut aussi déposer une version électronique de ce rapport sur le BV (dossier SPA), à raison
d’un exemplaire par binôme ou trinôme.
• En ce qui concerne le rapport de stage de pratique accompagnée, peut-on le faire de façon
individuelle s’il est difficile de trouver des disponibilités communes aux deux stagiaires et qu’il est
donc difficile de le faire à 2 ?
♠ Je n’ai pas rempli le quota d’heures du SPA.
Merci de signaler les cas particuliers, si ce n’est pas déjà fait, au secrétariat.
♠ Au sujet du rapport de SPA rédigé par le tuteur, on lui demande de renseigner : 1) le nombre
d’heures (du professeur stagiaire) en intervention devant les élèves ; 2) le nombre d’heures
« d’entretien » stagiaires-tuteur. Ma question est : où sont comptabilisées les heures de présence en
classe en observation ? Car pour le moment, ma tutrice m’a compté 3 heures d’intervention et 7
heures d’entretien. Elle ne savait pas où stipuler les heures d’observation simple.
Il semble qu’effectivement rien n’ait été prévu dans le modèle de document pour indiquer le
nombre total d’heures de travail.
Î Sur les projets (GSF de Roland Pouget)
• Je me pose […] beaucoup de questions en ce qui concerne le projet que l’on traite sur le
handicap :
− Comment doit-on le présenter ?
− Quelle doit-être le nombre de pages approximatif du rapport ?
− Doit-on y joindre un cahier de bord (présentant toutes nos heures de travail) ?
− Peut-on aller voir des centres (par exemple l’institut des jeunes aveugles) ? Et pour ce faire, a-t-
on besoin d’un papier de l’IUFM ou est-ce que je peux juste prendre contact directement avec eux
pour voir leurs méthodes de travail ?
Î Sur le travail d’étude et de recherche (TER) menant à la rédaction du mémoire
• Pourrait-on avoir plus d’exemples concrets sur l’organisation mathématique d’une séance ?
• Nous aurions besoin d’indications sur la façon de présenter l’organisation didactique de notre
mémoire.
♠ Est-ce un défaut si, en analysant une activité, on s’aperçoit que le moment exploratoire survient
après une suite de questions élémentaires mais longues à traiter, repoussant ce moment en fin de
séance (ce qui laisse ensuite peu de place pour les autres moments) ?
S’il s’agit de l’analyse d’une activité dans le cadre du mémoire, ce n’est pas cela qu’on va
évaluer : il vaut évidemment mieux que la séance observée ne soit pas « catastrophique », mais ce
n’est pas cette séance qui va être évaluée. C’est le travail d’étude et de recherche que le trinôme
PLC2Maths0809_Seminaire6 4

va effectuer − c’est-à-dire l’observation, l’analyse, l’évaluation et le développement − qui sera
l’objet d’une évaluation par le jury de soutenance.
♠ Pour le mémoire, est-il demandé de rédiger un nombre de pages minimum ?
Des précisions seront apportées lors de la prochaine séance du séminaire.
♠ Je n’ai toujours pas compris ce qu’allait être le développement dans le mémoire.
Cette partie du travail d’étude et de recherche sera abordée très prochainement.
• Comment prendre en compte dans l’organisation mathématique des questions préliminaires ?
Exemple : construction de points pour la droite d’Euler.
Î Sur les organisations mathématiques
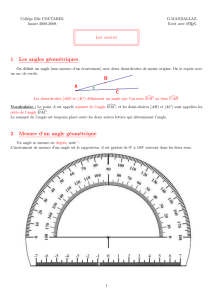
♣ En 6e, on aborde les angles sans parler d’orientation. Comment réagir si un élève nous demande
comment savoir si cet angle est l’angle rentrant ou saillant pour ABC ? (à part en dessinant
l’angle dont on parle).
A
B
C
♣ Quand peut-on faire des abus de notations ? « Carré de côté 5 cm ».
♣ Pour la démonstration du théorème de Pythagore, dans beaucoup de manuels on admet que
EFGH est un carré. Faut-il le démontrer ou est-il suffisant de l’admettre ?
c
c
c
c
• Lors de l’utilisation du théorème de Pythagore, faut-il raisonner avec des grandeurs (on se
retrouve alors avec AB2 = ...cm2 ) ou avec des mesures (on se retrouve alors avec AB = 3)?
• En ce qui concerne le théorème de Pythagore, faut-il faire intervenir les unités lors des calculs de
longueurs (pour la cohérence). Par exemple : « AB2 = 25 cm2 et donc AB = 25 cm2 = 5 cm. »
• Doit-on imposer les calculs avec les unités ? ou bien avec les mesures ?
• Comment introduire « les grandeurs et mesures » à des élèves qui n’ont pas fait de distinctions
entre ces notions l’année précédente ?
• Doit-on sanctionner les calculs effectués uniquement avec les mesures ? ou acceptons-nous les
deux formes de raisonnement ?
Les questions sur les grandeurs seront abordées ultérieurement.
Î Sur les organisations didactiques
• Est-on obligé de démontrer « la quatrième proportionnelle » en 5e ou peut-on la montrer
uniquement sur un exemple ?
PLC2Maths0809_Seminaire6 5