Redressement monophasé commandé

Redressement monophasé commandé C.P.G.E-TSI-SAFI
Mr BENGMAIH - 1 -
Redressement monophasé commandé
Introduction :
Un montage redresseur commandé permet d’obtenir une tension continue réglable à
partir d’une tension alternative sinusoïdale. L’utilisation de composants tels que les thyristors
permet de réaliser des redresseurs dont la tension moyenne de sortie peut varier en fonction de
l’angle de retard à l’amorçage.
I. Redressement monophasé simple sur charge résistive pure R :
On considère que le thyristor est parfait. φ est appelé angle de retard à l’amorçage. Il est
synchronisé sur le réseau. Il correspond à un temps de retard à l’amorçage
.
2
T
t
ϕ
ϕ
π
=.
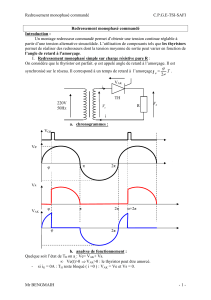
a. chronogrammes :
b. analyse de fonctionnement :
Quelque soit l’état de TH on a : Ve= VAK+ Vs.
• Ve(t)>0
⇒
VAK>0 : le thyristor peut être amorcé.
- si iG = 0A : TH reste bloqué ( i =0 ) : VAK = Ve et Vs = 0.
i
R
i
TH
V
AK
S
V
e
V
220V
50Hz
φ
VAK
VGK
Ve
wt
φ+2π
2π
2π
π
2π
π
φ
φ
Vs

Redressement monophasé commandé C.P.G.E-TSI-SAFI
Mr BENGMAIH - 2 -
- Si une impulsion de courant iG suffisante apparaît sur sa gâchette alors TH devient
passant et VAK =0, Vs = Ve et iD =
Ve
R
.
• Ve(t) =0
⇒
i =0A : le thyristor se bloque naturellement.
• Ve(t) < 0
⇒
VAK>0 : le thyristor ne peut pas être amorcé. Il est bloqué
même si une impulsion de courant apparaît sur sa gâchette.
Remarques :
• Vs, i et VAK ont la même période que Ve
⇒
2π rad.
• Le thyristor doit supporter en inverse VM.
• Le courant
S
V
i
R
=s’annule périodiquement, nous sommes en régime de conduction
discontinu.
• En pratique pour s’assurer qu’un thyristor s’amorce, on envoie sur sa gâchette un train
d’impulsions. c. valeur moyenne de la tension redressée :
Calculons la valeur moyenne <Vs> de vs(t) :
( ) ( ) ( )
2 2
0 0
1 1
. . sin .
2 2
TM
s S S
V
V V t dt V d d
T
π π
ϕ
θ θ θ θ
π π
= = =
∫ ∫ ∫
( )
cos
2
M
s
V
V
π
ϕ
θ
π
⇒= −
( ) ( )
(
)
1 cos
cos cos .
2 2
M
s M
V
V V
ϕ
π ϕ
π π
+
⇒= − + =
  .
Remarques :
• la valeur moyenne de la tension Vs peut être ajustée en fonction de l’angle de retard à
l’amorçage φ.
•
(
)
1 cos
.
2 .
S
D M
V
i V
R R
ϕ
π
+
= = .
Traçons l’allure de
(
)
S
V f
ϕ
= pour
0 2
ϕ π
≤ ≤
. Donc:0
M
S
V
V
π
≤ ≤ .
II. Redressement monophasé sur charge RL :
Avant l’instant d’application de l’impulsion de commande à t = t0, le thyristor est bloqué
0
i
⇒=
d’où : Vs = 0 ; mais lorsque l’impulsion est appliquée : Th est fermé
0
AK
V
⇒ =
( )
sin ( )
e M
di t
V V wt Vs Ri t L
dt
⇒= = = +

Redressement monophasé commandé C.P.G.E-TSI-SAFI
Mr BENGMAIH - 3 -
Si
( 0) 0
i t
= =
alors :
( ) ( )
( )
0
( )
L
22
( ) sin sin
L
Rt t
M
V
i t e wt
w R
ϕ ϕ
− −
⇒= + −
+
.
Donc le thyristor ne se bloquera que lorsque le courant s’annule.
Remarque : il y a apparition d’une partie négative au niveau de la tension d’entrée
qu’on peut éviter avec l’emploi d’une diode de roue libre.
III. Redressement monophasé double sur charge résistive pure R :
On prendra l’exemple d’un redresseur double alternance à deux thyristors et transformateur à
point milieu.
À t1 on amorce Th1 (modulo T)
À t1+T/2 on amorce Th2 (modulo T)
Ve
220V
50Hz
Vs
i
R
i
TH
VAK
L
-V
M
+V
M
t
VAK
V
e
T/2 t
0
+2T t
0
+T t
0
+V
M
2T T T/2
-V
M
+V
M
2T
T
T/2
-V
M
2T T T/2
t
t
t
V
s

Redressement monophasé commandé C.P.G.E-TSI-SAFI
Mr BENGMAIH - 4 -
R
i2
Th2
Th1
VT2
VT1
1
i
R
V
R
i
v
v
220V
50Hz
sin 2 50
R
M R
V
v V wt w f f Hz i
R
π = = = =
M
V
R
1
i
M
V
R
R
i
T t
1
-2V
M
t
t
t
1
+T/2
V
GK1
V
GK2
-VM
+V
M
+V
M
-V
M
+V
M
2T T t
1
2T T t
1
2T T T/2
T/2 t
1
+2T t
1
+T
t
1
+T/2
t
1
t
t
t
t
t
v
R
V
VT1

Redressement monophasé commandé C.P.G.E-TSI-SAFI
Mr BENGMAIH - 5 -
En posant θ = wt et θ
1 = wt1 :
• Pour
0
θ π
≤ ≤
:
(
)
1
0
V t
>
et
(
)
2
0
V t
<
:
Par conséquent :
1 1
0
TH H
V T
>⇒
peut être amorcé ;
2 2
0
TH H
V T
<⇒
ne peut pas être amorcé même en présence
d’impulsion.
Tant que
1
,
H
T
θ ϕ
<
et
2
H
T
sont bloqués :
1 2
0
R
i i i
= = =
;
0
R
V
=
;
1
0
T
V v
= >
;
2
0
T
V v
= − <
.
A
θ ϕ π
= <
, on amorce T
H1
, alors:
1
0
T
V
=
;
0
R
V v
= >
;
1R
v
i i
R
= =
;
2
0
i
=
;
2
2. 0
T
V v
= − <
.
• Pour
θ π
=
: v =0 : i
S
=i
TH1
=0
⇒
T
H1
se bloque naturellement.
• Pour
(
)
1
2 : 0
V t π θ π
≤ ≤ <
et
(
)
0
v t
<
:
Par conséquent :
1 1
0
T H
V T
< ⇒
ne peut être amorcé ;
2 2
0
T H
V T
> ⇒
Peut être amorcé.
Tant que
π θ ϕ π
≤ ≤ +
, T
H1
et T
H2
sont bloqués :
1 2
0
R
i i i
= = =
;
0
R
V
=
;
1
0
T
V v
= <
;
2
0
T
V v
= − >
.
A
2
θ π ϕ π
= + <
, on amorce T
H2
, alors:
2
0
T
V
=
;
0
R
V v
= − >
;
2R
v
i i
R
−
= = ;
1
0
i
=
;
1
2. 0
T
V v
= <
.
• pour
2
θ π
=
: v = 0 : i
S
=i
TH2
=0
⇒
T
H2
se bloque naturellement.
Remarques :
le courant i
R
s’annule : régime de conduction interrompu.
Chaque thyristor doit supporter en inverse une tension qui dépend de φ mais ≤ 2.V
M
.
Fonctionne seulement si φ≤π .
Valeur moyenne de la tension redressée :