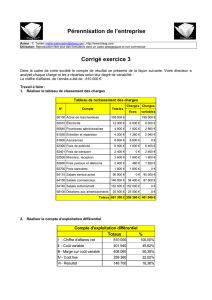
Rentabilité et Risque, Chap 11

Page 1
Rentabilité et Risque, Chap 11
Université Paris-Dauphine
Jacques HAMON 2013 Master 1
UE 106
1QuittersuiteLex <
<| >
Menu : le bêta (1)
1. Question : série sur le coefficient bêta ou sensibilité
2. Donnez trois expressions du bêta
3. Risque de marché (11-1 c)
4. Bêta et calculs sur historiques de cours (11-2 c)
5. Bêta de portefeuille (11-3)
6. Rentabilités et bêta (11-4)
7. Bêta et 4 scenarii (11-5 c)
8. Risque diversifiable & non diversifiable (11-6)
9. Bêta Alcatel en 2002 (11-7)
10. Bêta mensuels Renault et les autres, 1999-2000 (11-8c)
11. Bêta Axa en 1989-1990 (11-9)
12. Calcul du bêta d’un portefeuille (11-10)
Diapo
11-14
2QuittersuiteLex <
<| >
Menu : le bêta (2)
17. Blume à Paris (11-11)
18. Corrélations sur périodes adjacentes (11-12)
19. Bêta pour experts (11-13)
20. Bêta LVMH (11-14)
Extensions
20. Bêta et effet d’intervalle
21. Bêtas et longueur de la période de calcul ou stabilité du
bêta
22. Bêtas prévisionnel : analyse de scénari
23. Bêta et choix d’un indice
24. Bêta ajusté
Diapo
1-13

Page 2
Rentabilité et Risque, Chap 11
Université Paris-Dauphine
Jacques HAMON 2013 Master 1
UE 106
3QuittersuiteLex <
<| >
Questions, fin de chapitre 11
1. Le risque systématique d’un titre est-il égal à son bêta ?
2. Un portefeuille bien diversifié a-t-il un bêta nul ?
3. On sait que σ
=β ×σ +σ
. Cette identité implique-t-elle que l’identité suivante soit également
vérifiée, σ?=?β
×σ +σ?
4. Pour une action A, est de 0,9 et =40 %, l’action B a un bêta de 1,2 et une volatilité de 25 %.
De A ou B, quelle est l’action la moins risquée ?
5. Le bêta d’un portefeuille est-il égal à la moyenne pondérée des bêtas des titres en portefeuille ?
6. Au premier trimestre de l’an 2000, était-il possible de constituer un portefeuille d’actions tel que le
bêta du portefeuille soit nul ?
7. Le risque systématique d'un marché est-il le même d'un pays à l'autre ? Commentez.
8. Le risque systématique est-il constant au cours du temps dans un pays donné ? Commentez.
9. Fin février 2009, l’indice CAC40 touche 2 700 points. Vous vous souvenez de l’époque, pas si
lointaine, où il dépassait 6 000 et vous vous dites que le retournement de tendance arrive avec la
croissance. Bref vous êtes haussier. La connaissance du bêta des actions peut-elle vous être d’une
utilité quelconque dans la constitution de votre portefeuille ? Détaillez une démarche possible.
10. Fin février 2009, comment utiliser les connaissances vues dans ce chapitre pour constituer deux
portefeuilles différents dont on peut être à peu près sûr que l’un des deux figurera en très bonne
place dans le palmarès des fonds gérés collectivement à horizon de un an ?
Menu
Diapo
6QuittersuiteLex <
<| >
Bêta : calculs sur historiques de cours (11-2)
Ci contre, les cours de
trois actions et d’un indice
sur un an.
Mois Indice Cours de A Cours de B Cours de C
1 92 430 1020 712
2 91 420 1020 716
3 90 380 1021 718
4 94 385 1019 695
5 96 395 1020 692
6 101 430 1021 661
7 105 455 1020 660
8 105 476 1019 658
9 107 480 1022 630
10 109 510 1021 610
11 111 521 1025 610
12 121 580 1026 580
1. Calculer les βdes actions A, B et C.
Concluez en faisant apparaître les covariances (corrigé)
2. Calculez de la manière la plus simple possible le B d’un portefeuille composé de 25%
de A, 50% de B et 25% de C. Existe-t-il une autre méthode de calcul? (corrigé)
3. Peut-on combiner A, B et C pour obtenir un portefeuille zéro- β? (corrigé)
Existe-t-il une solution unique ? (corrigé)
Diapo Menu
À la main
Avec excel
En calcul matriciel

Page 3
Rentabilité et Risque, Chap 11
Université Paris-Dauphine
Jacques HAMON 2013 Master 1
UE 106
12 QuittersuiteLex <
<| >
Bêta de portefeuille (11-3)
1. Dans quelles proportions faut-il combiner les titres A et
B pour obtenir un portefeuille dont le taux de rentabilité
espéré sera de 20%? (corrigé)
2. Quel sera le βd’un tel portefeuille? (corrigé)
Titre
Taux
rentabilité
espéré
β
A 15% 0.82
B 28% 1.75
Diapo Menu
14 QuittersuiteLex <
<| >
Rentabilités
et bêta (11-4)
Au cours des 11 dernières années, on a relevé les données ci dessus (I l’indice; P
les cours, D les dividendes, RFle taux sans risque)
1. Calculez la moyenne, la variance et l’écart-type des taux de rentabilité du marché
(corrigé)
2. Calculez la moyenne, la variance et l’écart-type des taux de rentabilité du titre i (corrigé)
3. Calculez la covariance entre les taux de rentabilité du titre i et ceux du marché (corrigé)
4. Calculez le βdu titre i (corrigé)
Année I
m,t
D
m,t
/ I
m,t-1
P
i,t
D
i,t
/ P
i,t-1
R
f,t
1989 55.85 48
1990 66.27 0.0298 49 0.05 0.03
1991 62.38 0.0337 52 0.06 0.03
1992 69.87 0.0317 74 0.05 0.03
1993 81.37 0.0301 90 0.05 0.04
1994 88.17 0.03 102 0.05 0.04
1995 85.26 0.034 87 0.05 0.04
1996 91.93 0.032 78 0.05 0.05
1997 98.7 0.0307 81 0.05 0.05
1998 97.84 0.0324 71 0.06 0.07
1999 83.22 0.0383 70 0.05 0.06
Diapo Menu

Page 4
Rentabilité et Risque, Chap 11
Université Paris-Dauphine
Jacques HAMON 2013 Master 1
UE 106
16 QuittersuiteLex <
<| >
Bêta & 4 scenarii (11-5)
On dispose des observations suivantes concernant le taux
de rentabilité d’un titre i et du marché :
1. Calculez : E(Ri), E(Rm), σ²(Ri), COV(Ri, Rm) (corrigé)
2. Quelle est la sensibilité du titre i ? (corrigé)
3. Définissez et indiquez pour le titre i :
la valeur du risque total (corrigé)
la valeur du risque systématique (corrigé)
la valeur du risque spécifique (corrigé)
Etat Rm,t Ri,t
1 10% 9%
2 10% 9%
34% 4%
44% 2%
Diapo Menu
18 QuittersuiteLex <
<| >
Risque non diversifiable (11-6)
On vous donne les éléments suivants :
– Taux sans risque : 8%
– Taux de rentabilité observé sur le portefeuille i : 13%
– Risque total du portefeuille i : 50%
– Taux de rentabilité espéré pour le marché : 12%
– Risque du marché : 30%
– Covariance entre les taux de rentabilité du portefeuille i et du marché :
0.135
Quelle sont les valeurs
Du risque diversifiable du portefeuille?
du risque non diversifiable du portefeuille i? (corrigé)
Diapo Menu

Page 5
Rentabilité et Risque, Chap 11
Université Paris-Dauphine
Jacques HAMON 2013 Master 1
UE 106
20 QuittersuiteLex <
<| >
Alcatel (11-7)
1. Calculez le bêta d’Alcatel.Corrigé
2. Calculez le risque diversifiable d’Alcatel. Corrigé
3. Le bêta sur un an est-il significativement
différent de zéro ? Corrigé
4. Le bêta calculé avec les données des 6 premiers
mois est-il significativement différent de celui
calculé sur la deuxième moitié de l’année 2002 ?
Corrigé
5. Quel est le bêta en 2003 et en 2004?
Date en
2002 Alcatel CAC40
4-Jan. 14,42% 2,31%
11-Jan. -10,47% -3,55%
18-Jan. -7,58% -2,07%
25-Jan. -2,19% 1,55%
1-Fév. 2,99% -0,58%
8-Fév. -7,92% -4,66%
15-Fév. 2,73% 2,91%
22-Fév. -12,09% -3,37%
1-Mars 5,70% 4,48%
8-Mars 13,08% 3,52%
15-Mars -7,64% -1,14%
22-Mars -2,74% 1,19%
28-Mars 1,25% 0,67%
5-Avr. -1,54% -2,04%
12-Avr. -9,09% -1,91%
19-Avr. 6,21% 2,55%
26-Avr. -5,45% -2,11%
3-Mai -9,72% -1,23%
10-Mai 2,23% -1,03%
17-Mai 6,32% 2,48%
24-Mai -5,45% -2,24%
31-Mai -8,31% -2,50%
7-Juin -10,20% -5,60%
14-Juin -10,00% -2,74%
21-Juin -10,30% -3,26%
28-Juin -15,88% 0,59%
5-Juil. -15,66% -2,00%
12-Juil. 2,86% -3,36%
19-Juil. 4,17% -3,76%
26-Juil. -22,22% -10,33%
2-Août -3,24% 4,46%
9-Août -0,39% 4,80%
16-Août -1,38% -0,93%
23-Août 25,65% 6,57%
30-Août -13,88% -6,44%
6-Sep. -17,78% -6,68%
13-Sep. -8,78% 2,22%
20-Sep. -38,27% -9,68%
27-Sep. 2,00% 1,38%
4-Oct. 0,39% -3,52%
11-Oct. 8,59% -1,75%
18-Oct. 54,68% 15,79%
25-Oct. -15,12% -6,33%
1-Nov. 35,62% 3,07%
8-Nov. -2,02% -1,09%
15-Nov. 9,90% 3,18%
22-Nov. 1,31% 3,69%
29-Nov. 10,19% 1,15% Diapo
23 QuittersuiteLex <
<| >
Bêta mensuel (11-8)
A partir des taux de rentabilité mensuels ci-dessus
1. Calculez le bêta de FTE (France Telecom) et de Renault avec le Cac40 (corrigé)
2. Calculez le bêta de FTE et Ingénico avec le IT50 (corrigé)
3. Calculez le bêta de FTE, Renault et Saint-Gobain avec le IT50 (corrigé)
4. Les bêtas Renault et FTE avec le Cac40 sont-ils significativement différents avec
un risque d’erreur inférieur à5%? (corrigé)
Cac40 IT 50 StoXX FTE Renault Ingénico ST Gob
1-Apr-99 1.4% -2.0% 2.4% -12.7% -24.8% 0.7% 2.2%
3-May-99 6.2% 6.0% 6.1% 3.4% 21.3% 7.0% 12.5%
1-Jun-99 -2.1% 2.0% -3.9% -3.2% -7.3% -5.0% -5.5%
1-Jul-99 6.6% 7.8% 5.3% 1.2% 18.3% 4.6% 3.2%
2-Aug-99 -6.2% -2.6% -5.3% -10.9% 13.5% -7.6% 5.1%
1-Sep-99 6.6% 4.7% 3.1% 11.7% 6.1% 6.7% 9.0%
1-Oct-99 -0.4% 3.3% -2.2% 10.1% -1.7% 2.8% -3.4%
2-Nov-99 6.2% 9.4% 7.0% 11.7% -3.2% -5.6% -6.3%
1-Dec-99 9.1% 30.3% 9.6% 24.8% -11.0% 24.9% 0.9%
3-Jan-00 13.3% 38.4% 12.6% 17.3% 10.4% 76.2% 13.5%
1-Feb-00 -5.4% 6.7% -3.8% -0.1% 11.4% 43.8% -22.2%
1-Mar-00 10.0% 41.5% 6.8% 30.0% -22.4% 152.8% -0.8%
31-Mar-00 -0.5% -16.2% 1.4% 2.3% 2.4% -38.9% -6.7%
Diapo Menu