Extrait n°5 : 2001 Antilles Guyane

Physique Appliquée Annales Baccalauréat : Redressement (1996 à 2003) Tale GET
Page 1/32
Extrait n°1 : Métropole 2003
Partie B : Moteur à courant continu alimenté par un pont tout thyristors
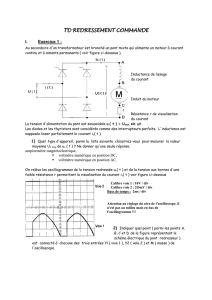
I Moteur à courant continu
On relève sur la plaque signalétique du moteur les indications suivantes
- Induit : 0,20 ; 20V ; 10 A.
- 160 W ; 1000 tr/min.
- Inducteur à aimants permanents.
- Machine compensée.
1. 1. On appelle E la force électromotrice du moteur et n sa vitesse de rotation exprimée en tr/min.
Montrer que l'on peut écrire E = k.n où k est un coefficient constant.
1.2. Pour le fonctionnement nominal, calculer 1. 2.
a. la puissance reçue par le moteur ; 1. 1. 2. b.
le rendement du moteur ;
1. 2. c. l'ensemble des pertes du moteur et en déduire la somme des pertes dans le fer et des
pertes mécaniques notée pc ;
1. 2. d. le moment du couple utile ;
1. 2. e. la force électromotrice.
1. 3. En déduire la valeur du coefficient k en précisant son unité.
II Pont tout thyristors
Le secondaire du transformateur alimente le pont dont le schéma est donné sur la figuré 2 de
l'annexe.
Les thyristors sont supposés parfaits. La commande des gâchettes n'est pas représentée. Une
sonde de courant de sensibilité 100 mV/A est utilisée pour visualiser à l'oscilloscope le courant
dans la charge. Simultanément, on visualise la tension u aux bornes de la charge. L'oscillogramme
obtenu est représenté sur la figure 3 de l'annexe 1.
La charge du pont redresseur est constituée de l'induit d'un moteur à courant continu à aimants
permanents et d'une bobine de lissage considérée comme parfaite.
La force électromotrice E du moteur est proportionnelle à la vitesse de rotation E = 1810–3n (E en V
et n en tr/min). La résistance de l'induit du moteur est R = 0,2 .
Le moteur entraîne une charge lui imposant un courant d'intensité supposée constante.
2. 1. Déterminer l'intensité i (supposée constante et égale à I) du courant dans la charge ainsi que
l'angle de retard 0 à l'amorçage des thyristors.
2.2. Représenter sur le document réponse 2 page :
2. 2. a. les chronogrammes de iTh1, iTh4 et i2 sur une période et en concordance de temps
avec la tension source u2 ;
2. 2. b. les intervalles de conduction des quatre thyristors sur une période.
2.3. Exprimer la tension u aux bornes de la charge en fonction de E, R et uL (tension aux bornes
de la bobine). Montrer que < u > correspond à la tension aux bornes de l'induit du moteur (<
u > désigne la valeur moyenne de la tension u).
2.4. La courbe < u > = f (0) est fournie sur la Figure 3 de l'annexe 2.
2. 4. a. Déterminer < u > pour le retard à l'amorçage de la question 2.1.
2. 4. b. En déduire la vitesse de rotation n du moteur.
Figure 1
u2
i2
iTh2
iTh4 iTh3
Th1
Th4
Th2
Th3
M
L
i = I
iTh1
u

Physique Appliquée Annales Baccalauréat : Redressement (1996 à 2003) Tale GET
Page 2/32
Figure 2
Calibre : 0,5 V/div
Zéros pour
les deux voies
Calibre : 10 V/div
Figure 3
0.0
5.0
10.0
15.0
20.0
25.0
010 20 30 40 50 60 70 80 90
<u>
(volts)
 (Degrés)

Physique Appliquée Annales Baccalauréat : Redressement (1996 à 2003) Tale GET
Page 3/32
Extrait n°2 : Métropole 2002

Physique Appliquée Annales Baccalauréat : Redressement (1996 à 2003) Tale GET
Page 4/32
Extrait 3 : Polynésie 2001
PARTIE A : Redressement
1 - Alimentation de l'inducteur.
Le circuit d'excitation d'un moteur à courant continu est alimenté par le circuit de la figure 2 de
l'annexe et permet d'obtenir une tension moyenne <u> = 160 V. Il est parcouru par un courant continu
Iex = 2A.
1 .1 . La tension appliquée à l'entrée du pont redresseur est une tension sinusoïdale v(t) de fréquence
50 Hz. Calculer sa valeur efficace.
1.2. Justifier que le courant d'excitation soit continu en précisant la nature du circuit d'excitation
(résistif, inductif, capacitif).
2 - Alimentation de l'induit.
Le circuit d'induit du moteur à courant continu est alimenté par le circuit de la figure 3 de l'annexe. La
tension d'alimentation du pont est v(t) = VMAX sin t, de fréquence 50 Hz. La tension moyenne <uc>
maximale est de 160 V. Le courant ic est continu. Sa valeur est : Ic = 22 A.

Physique Appliquée Annales Baccalauréat : Redressement (1996 à 2003) Tale GET
Page 5/32
2.1. De quel type de pont redresseur s'agit-il ?
2.2. Quel est l'avantage d'un tel pont par rapport au pont redresseur précédent.
2.3. Citer au moins un autre dispositif qui permettrait d'alimenter le moteur et d'obtenir le même
fonctionnement.
3 - Étude d'u n point de fonctionnement.
On note 0 l'angle de retard à l'amorçage en radian. Le thyristor Tl est amorcé pour 0<0<
Le thyristor T2 est amorcé avec un angle de retard à l'amorçage '0 = 0+ 
3.1. La valeur de l'angle de retard à l'amorçage 0 étant réglée à /4, compléter le tableau de
conduction des éléments du document réponse Figure 1. Hachurer les zones de conduction.
3.2. Indiquer l'allure de uc sur la Figure 2 du document réponse.
3.3. Dans quels intervalles a-t-on un phénomène de « roue libre » ?
3.4. Indiquer l'allure de l'oscillogramme de iT2 sur la figure 3 : la valeur de l'intensité dans l'induit étant
supposée constante et égale à Ic.
3.5. Indiquer sur la figure 4 du document réponse, un branchement de l'oscilloscope permettant de
visualiser simultanément uc et IT2.
4 - Valeurs particulières de 0.
4.1. On rappelle que < uc>
max
V
(1 + cos 0)
4.1 .1. Quelle est la valeur 1 de l'angle de retard à l'amorçage qui permet d'obtenir < uc> maximale ?
4.1 .2. Dans ces conditions, que vaut Vmax ?
4.1.3. Quelle est la valeur efficace V de v(t) ?
4.2. On veut obtenir < uc> = 40 V tout en maintenant Vmax à sa valeur précédente. Quelle
valeur 2 exprimée en radian doit-on donner à l'angle de retard à l'amorçage ?
Figure 2
Figure 3
DOCUMENT-REPONSE