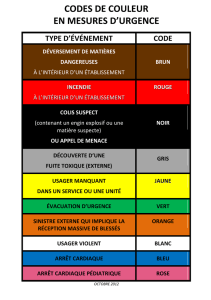
Fiche synthèse sur la régression linéaire multiple

SCI6060A – Cours 11 (25 mars 2011)
Professeure : Christine Dufour
Régression linéaire multiple
L'analyse de régression linéaire multiple permet d'examiner le lien entre une variable dépendante et plusieurs variables
indépendantes pour ultimement faire des prédictions. Par exemple, soit le ratio de documents par usager au sein des
bibliothèques membres de l’ARL
1
, le ratio de dépenses par usager et finalement le ratio d’emprunts par usager. Peut-on
expliquer le ratio documents par usager en fonction des ratios dépenses par usager et emprunts par usager? Si oui, comment?
Pour le savoir, il faut faire une analyse de régression linéaire multiple en utilisant le ratio documents/usager comme variable
dépendante (Y) et les ratios dépenses/usager et emprunts/usager comme variables indépendantes (X).
1
Source : ARL Statistics and Performance Measures, 1999 [http://www.arl.org/stats/arlstat/indi99.pdf]
Analyse de régression linéaire multiple dans Excel [Utilitaire d'analyse – Régression linéaire]
Résultats retournés par Excel avec l'utilitaire d'analyse Régression linéaire
Statistiques de la régression
Coefficient de
détermination
multiple 0,930931867
Coefficient de
détermination R^2 0,866634141
Coefficient de
détermination R^2 0,864164403
Erreur-type
50,07808443
Observations
111
ANALYSE DE VARIANCE
Degré de liberté
Somme des carrés
Moyenne des carrés
F
Valeur critique de F
Régression 2 1759990,41 879995,203 350,901228 5,65473E-48
Résidus 108 270843,97 2507,81454
Total 110 2030834,38
Coefficients
Erreur-type Statistique t Probabilité Limite inférieure pour seuil de confiance = 95%
Limite
supérieure
pour seuil de
confiance =
95%
Limite
inférieure
pour seuil
de
confiance =
95,0%
Limite
supérieure
pour seuil
de
confiance =
95,0%
Constante 8,549465992
9,76892105 0,87516993 0,38342363 -10,81422971 27,91316169 -10,8142297 27,9131617
RATIO
DEPENSES/
USAGER 0,144238628
0,0055569 25,9566937 3,1268E-48 0,133223898 0,155253358 0,1332239 0,15525336
RATIO
EMPRUNTS/
USAGER -4,42884773
5,48560875 -0,80735757 0,42123506 -15,30227562 6,44458016 -15,3022756 6,44458016
Coefficient de corrélation (r)
Valeur = 0,93, donc une relation forte entre les variables. On
ne parle pas ici de sens de la relation (directe ou inverse)
car ce n'est pas d'une droite dont il s'agit… mais d'un objet
linéaire à n dimensions, où n = nombre de variables
indépendantes + 1
Coefficient de détermination R^2
(carré du coefficient de corrélation)
Proportion de Y qui peut être expliquée par les X (pourcentage)
Plus c'est élevé, plus les X sont utiles pour expliquer Y
Ici : = 87% c'est-à-dire que les variations du ratio documents/usager s'expliquent
à 87% par les variations des emprunts/usager et des dépenses/usager.
Constante de la courbe
de régression (b0)
Coefficient de la variable
indépendante X1 (b1)
Ici, la courbe de régression serait (en utilisant les coefficients b0, b1 et b2): Y = b0 + b1X1 + b2X2 = 8,55 + 0,14X1 -4,43X2
Ce qui se traduit par : Ratio de documents/usager = 8,55 + 0,14 * Ratio dépenses/usager - 4,43 * Ratio emprunts/usager
Utilité? Pour faire des prédictions! Par exemple, quel ratio de documents/usager peut-on s'attendre pour une bibliothèque
ayant un ratio de dépenses par usager de 500 $/usager et un ratio d'emprunts/usager de 3 docs/usager ?
= 8,55 + 0,14 * 500 - 4,43 * 3 = 65,26 docs/usager.
Valeur critique de F
Permet de vérifier si le lien observé est significatif ou
simplement dû au hasard. Si plus petit ou égal au
seuil critique, c'est significatif; sinon c'est dû au
hasard. Habituellement on prend un seuil critique de
0,05 (5%). Ici : =5,65E-48 < 0,05 donc c'est
significatif, il y a bien un lien entre les deux
variables. On peut continuer l'analyse en toute
légitimité.
Coefficient de la variable
indépendante X2 (b2)
L’analyse de régression
linéaire multiple produisant
un objet linéaire en n
dimensions, Excel ne peut
le représenter directement
graphiquement. Il produit à
la place des graphiques en
deux dimensions, un par
variable indépendante,
mettant en lien la variable
dépendante et chacune des
variables indépendantes.
On ne cherche pas ici à
surimposer une droite.
RATIO EMPRUNTS/ USAGER Courbe de régression
0
100
200
300
400
500
600
700
800
900
01234567
RATIO EMPRUNTS/ USAGER
RATIO DOC/ USAGER
RATIO DOC/ USAGER Prévisions RATIO DOC/ USAGER
RATIO DEPENSES/ USAGER Courbe de régression
0
100
200
300
400
500
600
700
800
900
0 1000 2000 3000 4000 5000 6000
RATIO DEPENSES/ USAGER
RATIO DOC/ USAGER
RATIO DOC/ USAGER Prévisions RATIO DOC/ USAGER