Baccalauréat L spécialité La Réunion septembre 2007

Baccalauréat L spécialité La Réunion septembre 2007
Exercice 3 6 points
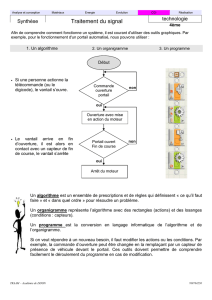
Une entreprise de recyclage récupère un lot de digicodes ayant tous un clavier identique à
ce-lui représenté ci-contre.
Chacun de ces digicodes a été programmé pour fonctionner avec un code constitué de deux
signes choisis parmi les douze figurant sur ce clavier.
Par exemple A0, BB, 43 sont des codes possibles.
Pour remettre en état de fonctionnement un tel digicode, il faut retrouver son code.
Pour faciliter une telle recherche, a été inscrit sur le boîtier de chaque digicode un nombre
R qui dépend du code. Ce nombre a été obtenu de la manière suivante :
• Le code est considéré comme un nombre écrit en base 12. A est le chiffre dix et B le chiffre 11.
• Le nombre R inscrit sur le boîtier est le reste de la division euclidienne du code, converti en base 10, par 53.
R est donc un nombre écrit en base 10 et tel que 0 R 53.
1° Combien y a-t-il de codes possibles ?
2° On suppose que le code d’un digicode est AB.
a) Ecrire en base 10 le nombre dont l’écriture en base 12 est (AB)douze.
b) Déterminer le nombre R inscrit sur le boîtier de ce digicode.
3° Sur le boîtier d’un digicode est inscrit le nombre R égal à 25.
Démontrer que (21)douze peut être le code de ce digicode.
4° On considère l’algorithme suivant :
Entrée :
R un entier naturel.
Initialisation :
L liste vide ;
Traitement :
Tant que 53 n + R  143, mettre dans la liste L la valeur de 53 n+ R puis ajouter 1 à n.
Sortie :
Afficher la liste L.
a) Faire fonctionner cet algorithme pour R = 25.
b) On suppose que le nombre R inscrit sur le boîtier d’un digicode est R = 25.
Quels sont les trois codes possibles de ce digicode ?
5° Dire si l’affirmation suivante est vraie ou fausse. Si l’affirmation est considérée comme étant fausse, en apporter
la preuve.
Affirmation : quelle que soit la valeur de R l’algorithme permet de trouver trois codes parmi lesquels se trouve le
code secret.
CORRECTION

Exercice 3 6 points Une entreprise de recyclage récupère un lot de digicodes ayant tous un clavier
identique à ce-lui représenté ci-contre. Chacun de ces digicodes a été programmé pour fonctionner avec
un code constitué de deux signes choisis parmi les douze figurant sur ce clavier. Par exemple A0, BB, 43
sont des codes possibles. Pour remettre en état de fonctionnement un tel digicode, il faut retrouver son
code. Pour faciliter une telle recherche, a été inscrit sur le boîtier de chaque digicode un nombre R qui
dépend du code. Ce nombre a été obtenu de la manière suivante : • Le code est considéré comme
un nombre écrit en base 12. A est le chiffre dix et B le chiffre 11.
• Le nombre R inscrit sur le boîtier est le reste de la division euclidienne du code, converti en
base 10, par 53. R est donc un nombre écrit en base 10 et tel que 0
R
53.
1° Combien y a-t-il de codes possibles ?
Il y a 12 choix possibles pour le premier signe et 12 pour le second donc il y a 144 codes possibles.
12  12 = 144.
2° On suppose que le code d’un digicode est AB. a) Ecrire en base 10 le nombre dont l’écriture en base 12 est (AB)douze.
(AB)douze = 10  121 + 11  120 = 131
b) Déterminer le nombre R inscrit sur le boîtier de ce digicode.
131 = 25 + 2  53.
3° Sur le boîtier d’un digicode est inscrit le nombre R égal à 25. Démontrer que (21)douze peut être le code de ce digicode.
(21)douze = 1  120 + 2  121 = 25.
(AB)douze et (21)douze ont le même reste dans la division en base 12.
4° On considère l’algorithme suivant :
Entrée :
R un entier naturel.
Initialisation :
L liste vide ;
Traitement :
Tant que 53 n + R  143, mettre dans la liste L la valeur de 53 n+ R puis ajouter 1 à n.
Sortie :
Afficher la liste L.
a) Faire fonctionner cet algorithme pour R = 25.
R
L
n
53  n + R
53  n + R  143 ?
R = 25
L = { }
0
25
oui
L = {25}
1
78
oui
L = {25, 78}
2
131
oui
L = {25, 78, 131}
L = {25, 78, 131}
b) On suppose que le nombre R inscrit sur le boîtier d’un digicode est R = 25. Quels sont les trois codes possibles de ce digicode ?
Tous les éléments de la liste ont pour reste 25 dans la division par 53, ils correspondent donc à
tous des codes possibles. 25 correspond à 21, 131 correspond à AB et 78 à 66
78
12
6
6
5° Dire si l’affirmation suivante est vraie ou fausse. Si l’affirmation est considérée comme étant fausse, en apporter la preuve.
Affirmation : quelle que soit la valeur de R l’algorithme permet de trouver trois codes parmi lesquels se trouve le code secret.
53  n + R 143 53  n 143 – R
Si R = 52 alors il faut déterminer les valeurs de n solution de l'inéquation 53  n 143 – 52
53  n 143 – 52 53 n 91.
Il n'y a que deux valeurs possibles pour n : 0 et 1.
R
L
n
53  n + R
53  n + R  143 ?
R = 52
L = { }
0
52
oui
L = {52}
1
105
oui
L = {52, 105}
2
158
non
L = {52, 105}