professeur

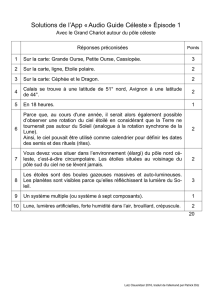
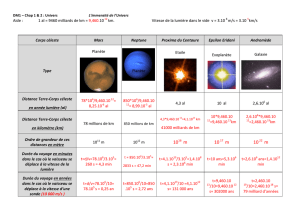
Nous nous sommes intéressés à la méthode utilisée par Kepler pour déterminer les orbites de la Terre et de Mars.
Cette méthode peut être exploitée en classe de Seconde au cours de l'enseignement d'exploration "Méthodes et
Pratiques Scientifiques" (thème : "Science et vision du monde") ou en Accompagnement Personnalisé.
Nous proposons, pour ce sujet, un diaporama expliquant la méthode de Kepler, ainsi que deux fiches élèves
illustrant cette méthode. Des documents geogebra viennent compléter ces fiches.
Ce diaporama est recommandé en introduction aux activités proposées.
La méthode de Kepler est ici expliquée avec des données actualisées (cf. Histoire de la Cosmologie, Régine
Eber, CRDP d'Auvergne 2003) .
Il est remarquable de constater que Kepler a pu étayer ses découvertes avec moins de valeurs et des durées entre
ses observations différentes de la période sidérale de Mars (temps nécessaire à Mars pour effectuer une révolution
autour du soleil, soit 687 jours, elle est de 365,256 jours pour la Terre).
Kepler a établi que l'orbite de la Terre est une ellipse dont le Soleil est un foyer mais en raisonnant d'abord sur une
trajectoire circulaire qu'il a ensuite réajustée de manière empirique. Dans le diaporama, la méthode est appliquée à
une trajectoire circulaire de la Terre autour du Soleil, l'excentricité de l'ellipse étant proche de 0 (La distance
centre-foyer est relativement faible) et on considère que les trajectoires de la Terre et de Mars sont coplanaires.
Prérequis :
Pour le repérage des astres dans l'univers, on choisit une direction de référence visant le point gamma (point
vernal : cf. complément en fin de fiche), on la note ici "direction
γ
".
On mesure l'angle
(
)
SMS ;
0
γλ = que fait la direction
γ
avec l'axe Soleil-Mars à une date donnée (ici
22/01/1978).
Une méthode "facile" d'obtention de
0
λ
consiste à mesurer, depuis la Terre évidemment, l'angle de cette direction
γ
avec l'axe Soleil-Terre-Mars lors d'une opposition Soleil-Mars (écart de 12 heures entre l'observation du Soleil
et celle de Mars dans le même méridien terrestre).
0
λ
étant établi (environ 122° dans l'exemple du diaporama), on retrouve cette même position de l'axe Soleil-Mars
par rapport à la direction
γ
tous les 687 jours (période sidérale de Mars).
Méthode de Kepler :
Ceci étant posé, pour connaître la position de la Terre par rapport au Soleil et à Mars, il suffit alors de prendre la
mesure de deux angles
(
)
TMT
M
; γλ = et
(
)
TST
S
; γλ = depuis la Terre à des intervalles de 687 jours.
Dans les diapositives du diaporama, le point jaune représente le Soleil S , le point bleu la Terre T et le point orange
la planète Mars M .

λ
0
λ
M
λ
S
λ
M
θ
β
θ = λΜλ0β = λ−− λ0
°
λ
λλ
λ °
°
λ
λλ
λ °
Dans la diapositive ci-contre :
On part donc d'une opposition
(alignement S-T-M ) visible le 22/01/1978.
Ce jour-là :
(
)
°≈=== 122;);(
0 M
TMTSMS λγγλ
et
(
)
°+== 180;
0
λγλ TST
S
[360°].
687 jours plus tard (le 10/12/1979) :
Mars est revenu à la même position (elle
a fait un tour), la Terre n'est plus alignée
avec S et M (1,88 tour autour de S ).
On a alors :
(
)
°≈= 122;
0
SMS γλ à nouveau
et on mesure depuis le Terre :
(
)
°≈= 158; TMT
M
γλ
,
et
(
)
°≈= 257;TST
S
γλ
.
On peut alors, en fixant S et M dans le plan et sachant que les vecteurs
γ S
,
γ M
et
γ T
sont colinéaires de même
sens, positionner T à cette date :
(
)
(
)
°+== 180;;
M
MTTMTM λγγ
[360°] et
(
)
(
)
[
]
°°+== 360180;;
S
STTSTS λγλ
, puis on réitère la
construction.
Kepler va plus loin en calculant les angles
β
et
θ
dans le triangle STM :
(
)
STSM ;= β
et
(
)
MTMS ;= θ
.
(
)
(
)
(
)
(
)
[
]
°+−°=+°+−=+== 360180;180;;;
00 S
TSTSTTSSMSTSM λλγλγγβ
,
(
)
(
)
(
)
(
)
(
)
[
]
°+−=+=+== 360;;;;;
0 M
TMTSSMMTTSMSMTMS λλγγγγθ .
( Avec la relation de Chasles et les égalités
(
)
(
)
[
]
π
π
2;;
+
=
−
vuvu
et
(
)
(
)
[
]
π
2;; vuvu
=
−
−
au programme
de Mathématiques de première S .)
On suppose connue l'orbite de la Terre.
Dans la diapositive ci-contre :
Le 18/05/1976, on mesure :
(
)
°≈= 237; STSL
T
γ
( obtenu à l'aide du calcul :
(
)
(
)
TSTSTTL
T
;180; γγ +°== ,
[
]
°
+
°
=
360180
S
λ
),
et
(
)
°≈= 121;TMT
M
γλ .
387 jours plus tard, Mars est revenue à
la même position, la Terre a effectué
1,88 tour (1 tour + 317° ou 2 tours – 43°)
et se trouve en position T '.
On recalcule :
°
≈
195'
T
L
(ce qui correspond presque à 237° – 43° : la trajectoire elliptique est quasi-circulaire), et on mesure
°
≈
118'
M
λ
.

On traçant les demi-droites d'origine T et T ' et formant respectivement les angles
M
λ
et
' M
λ
avec la direction
γ
,
on obtient une position de Mars.
En réitérant les observations et constructions avec des couples de dates distantes de 687 jours, on obtient des
positions différentes de Mars et donc sa trajectoire.
 !"
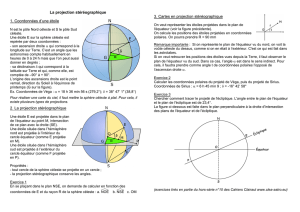
Cette activité permet de comprendre la méthode de Kepler en la simplifiant : la direction du Nord remplace la
direction
γ
, et la position de l'axe ( AB ) est toujours fixe par rapport au Nord (pas de période à prendre en
considération).
Par la mesure de deux angles pris depuis le bateau d'Ulysse (noté U ), on peut déterminer exactement les mesures
des angles du triangle ABU , ici :
(
)
AUAB ;= θ et
(
)
BUBA ;= β .
Pour des élèves de seconde, les angles orientés ne figurent pas au programme de Mathématiques, les élèves
peuvent toutefois s'appuyer sur le schéma pour les démonstrations.
 !#
Cette fiche a été réalisée d'après deux ouvrages de Kepler et expérimentée en Accompagnement Personnalisé en
classe de Seconde.
La première partie s'appuie sur l'ouvrage Mysterium cosmographicum (Le secret du monde) paru en 1596.
Elle présente la vision copernicienne de l'univers (modèle héliocentrique) et la modélisation de la position des
planètes du système solaire à l'intérieur des polyèdres réguliers : les solides de Platon (cf. diapo 2 du diaporama).
La seconde partie, qui est inspirée du traité Astronomie Nouvelle paru en 1609, présente également un problème
de localisation de bateau et une méthode de détermination de l'orbite de la Terre.
La différence avec la fiche élève 1 est que l'on ne cherche pas à déterminer les angles
θ
et
β
du triangle.
Pour la localisation du bateau, les mesures prises sont suffisantes pour le placer, sans calculs.
Pour l'orbite de la Terre, le soleil est remplacé par le point
α
(centre de l'ellipse) et M =
κ
.
Le calcul des données pour l'angle
α
κ
ˆ
T
a été fait en amont par Kepler, puisque l'angle Terre-Mars-alpha n'est
évidemment pas mesurable depuis la Terre.
On l'obtient par le calcul :
0
ˆ
λλθακ −==
M
T.
$%  
Nous présentons ici quelques définitions, glanées sur Wikipédia, qui donnent quelques précisions sur les termes
employés :
La sphère céleste est une sphère imaginaire dont le centre est occupé par la Terre. Ce concept astronomique,
hérité de l'Antiquité et du géocentrisme, permet de représenter tous les astres tels qu'on les voit depuis la Terre.
Ainsi, il est possible de positionner ceux-ci dans le ciel en leur attribuant des coordonnées uniques.
La partie visible de la sphère céleste, c'est-à-dire l'hémisphère surplombant l'observateur, est couramment
désignée par le terme voûte céleste .
Le système de représentation
Dans le système de représentation de la sphère céleste, la Terre est considérée comme immobile et c'est la sphère
céleste qui tourne autour de notre planète.
L'axe de rotation passe par les pôles géographiques, et ses intersections avec la sphère céleste déterminent les
pôles célestes. Ursae Minoris, plus connue sous le nom d'étoile polaire, est tellement proche du pôle nord
céleste qu'elle semble immobile dans le ciel.

Le grand cercle qui est l'intersection du plan équatorial avec la sphère céleste s'appelle l'équateur céleste. Cet
équateur partage la sphère céleste en deux hémisphères célestes nord et sud. D'une manière générale, on peut
projeter n'importe quel point de la Terre sur la sphère céleste ; la projection est l'intersection de la verticale passant
par ce point avec la sphère céleste. La verticale d'un point de la Terre, sauf pour les pôles, trace un parallèle sur
cette sphère au fur et à mesure de sa rotation.
Tous les astres peuvent être également représentés sur la sphère céleste, y compris le Soleil, et on appelle
écliptique le grand cercle qui est la projection de la trajectoire du Soleil sur la sphère céleste : c'est l'intersection
du plan de l'écliptique et de la sphère céleste.
L'inclinaison de l'axe de la Terre par rapport à l'écliptique fait que l'écliptique est aussi inclinée relativement à
l'équateur céleste. L'intersection de ces deux grands cercles est la ligne des équinoxes , qui coupe la sphère céleste
en deux points opposés qui sont les points équinoxiaux de printemps et d'automne. Quand le Soleil croise de la
sorte le plan équatorial, donc aux équinoxes, la durée du jour est égale à la durée de la nuit.
Le point équinoxial de printemps est aussi appelé le point vernal ou point Gamma . La direction de la ligne des
équinoxes de la Terre vers le point vernal désigne à l'infini une direction à peu près fixe* dans le système solaire
où elle fait office de référence pour le calcul de coordonnées astronomiques.
Un grand cercle passant par les pôles du monde, et dont le plan est dès lors perpendiculaire au plan de l'équateur
céleste, est appelé un méridien céleste.
* direction
γ
dans les explications du diaporama.
$&
- Mysterium cosmographicum (Le secret du monde), traité scientifique de Johannes Kepler (1596).
- Astronomia Nova (Astronomie Nouvelle), traité de Johannes Kepler (1609).
- Histoire de la Cosmologie, Régine Eber (CRDP d'Auvergne 2003)
- Cahiers Clairaut (bulletin de liaison quadri-annuel du CLEA : Comité de Liaison Enseignants Astronomes),
N°117 du printemps 2007, article de Blaise SIMON : "Comment Kepler a déterminé l'orbite de la Terre autour du
Soleil". L'article est téléchargeable à l'adresse : http://www.inrp.fr/Acces/clea/web/
- Logiciel Stellarium, logiciel gratuit d'observation de la voûte céleste, téléchargeable à l'adresse :
http://www.stellarium.org/fr/
- Les pommes de Newton, Jean-Marie Vigoureux (éditions Albin Michel Sciences).