Défis mathématiques

Dés mathématiques
Par Octavian Lecca, Académie DELFO
[email protected]
www.delfoacademy.com
Solutions aux pages 44 - 45
ENVOL no 145 — octobre-novembre-décembre 2008
8GRMS
Problème no 1
Trouvez les nombres naturels (a), (b), (c) et (d) dans les égalités :
a) 1000(d − 1) + 100(3 − c) + 10(1 − b) + a = 918;
b)
2,1 3, 2 0, 8 5, 4a b a b+ = +
si le chiffre (b) est le double du chiffre (a).
Problème no 2
Les résultats des opérations suivantes représentent les termes d’une suite :
Premier rang : (1 − 2) × (3 − 4) × (5 − 6) × ... × (99 − 100)
Deuxième rang :
( )
0 2 3
2
3 3 3 2 4 2 4
2 2 3 3
− − −
− × − ÷ × ÷ −
− × −
Troisième rang :
( )
( )
2
1aaaaaaa a
b b b b
++++++ ÷
÷+ + ÷
Quel rang représente le résultat des opérations suivantes :
( ) ( )
( )
98
19 17 17 19
999
2
3 17 19 19 17 3
7
6 6 6 7 7 6
× − ÷ − ×
÷ − − × −
?
Problème no 3
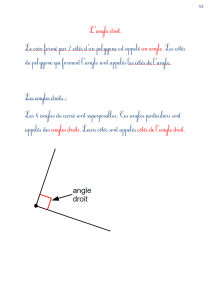
Étant donné un polygone régulier avec 30 côtés, trouvez :
a) la valeur de l’angle formé par deux côtés consécutifs;
b) la valeur de l’angle formé entre le premier et le cinquième côté;
c) si A, B et C sont 3 sommets consécutifs et si O est le centre du cercle
circonscrit au polygone,
OB
est perpendiculaire à
AC
;
d) deux côtés parallèles;
e) entre quels côtés on retrouve le plus petit angle et quelle est sa valeur?

Solutions des dés mathématiques
Par Octavian Lecca, Académie DELFO
[email protected]
www.delfoacademy.com
Solution du problème no 1
a) Si on fait la multiplication on obtient :
1000d + 100 × 3 + 10 × 1 + 1 × a -
(1000 × 1 + 100c + 10b + 1 × 0)
Cela représente la soustraction entre les nombres (d31a)
et (1cb0).
On peut écrire l’égalité de la manière suivante :
d 3 1 a
- 1 c b 0
9 1 8
On trouve facilement :
a = 8, b = 0, c = 4 et d = 2
b) Étant donné que le nombre des entiers à gauche de
l’égalité est le même que le nombre des entiers à
droite, nous pouvons les éliminer et réécrire l’égalité
uniquement avec les périodes (puisqu’elles sont de
deux chiffres partout). Donc :
(1a) + (b2) = (a8) + (4b)
Ou bien :
10 + a + 10b + 2 = 10a + 8 + 40 + b
9b – 9a = 36
Pour chaque (b), il y a 2 (a), donc on peut écrire :
9 × 2a − 9a = 36
On trouve :
a = 4 et b = 8
Solution du problème no 2
Premier rang : on observe qu’il y a 50 parenthèses,
chacune ayant la valeur (-1).
(-1)50 = 1
Deuxième rang : en appliquant premièrement les
exposants, on arrive a :
( )
( )
( )
1 9 27 4 4 ÷ 2 4
2 2 3 3
9 27 16 ÷ 2 4
2 6 3
36 36 3
8 4 12
4 3 7 7
− × − ÷ × − − − − =
− × −
− − ÷ − − − − =
− −
− −
÷ − − = ÷ =
− − −
Troisième rang :
( )
( )
2
2 2 2
1
7 3 3
1 1
3 7 7
aaaaaaa a
b b b b
a a
b b
++++++ ÷
÷ =
+ + ÷
÷
÷ = × =
÷
Calcul des opérations pour le rang inconnu :
( ) ( )
( )
98
19 17 17 19
999
2
98 98 99
999
3 17 19 19 17 3
7
6 6 6 7 7 6
3 1 3 3 3 3
6 6 7 1 7 7 7 7
−
× − ÷ − × =
÷ − − × −
× −
× = × =
− − × −
Comme la soustraction entre les nombres 1719 et 1917
représente la distance entre les nombres, la valeur de la
soustraction va être la même, peu importe le point de
départ. C’est seulement le signe qui va être différent.
Le résultat de la division entre deux nombres identiques
mais de signes différents est (-1).
La suite est :
0 1 2 99
3 3 3 3
7 7 7 7
Le dernier rang est le 100e rang.
ENVOL no 145 — octobre-novembre-décembre 2008
44 GRMS
Problèmes à la page 8

Solution du problème no 3
a) On applique la formule pour l’angle interne :
( ) ( ) 0
2 180 30 2 180 168
30
n
n
− × − ×
= =
b) Comme l’angle externe entre deux côtés consécutifs
est de 180 – 168 = 12° et comme entre le premier et le
cinquième côté, il y a 4 augmentations de 12°, l’angle
demandé est de 48°.
(une autre démonstration serait de construire des
parallèles aux 4 côtés consécutifs au sommet du premier
côté; l’augmentation de 12° pour chaque nouveau côté
serait évidente);
c) L’angle AOB est 360 ÷ 30 = 12°; le triangle AOC est un
triangle isocèle, avec l’angle O = 2 x 12 = 24°; l’angle
OAC = (180 – 24) ÷ 2 = 78°; si (D) est l’intersection entre
AC
et
OB
, alors la somme des angles intérieurs dans
le triangle AOD est de 180° (180° - 12° - 78° = 90°);
alors l’angle ADO est de 90°; OB est perpendiculaire
à AC;
ENVOL no 145 — octobre-novembre-décembre 2008 45
GRMS
d) Chaque côté du polygone forme un triangle isocèle avec
le centre (O). Les côtés parallèles du polygone sont
ceux qui ont les côtés de leurs triangles en prolongation,
parce que les angles alternes internes sont congrus. Les
côtés parallèles du polygone dans cette situation sont
les côtés opposés, par exemple le premier avec le 16e
côté. On peut aussi calculer combien de côtés il y a
entre les côtés parallèles en calculant combien de fois
12 entre en 180 : il y a 15 côtés entre les parallèles.
e) Entre un côté et le côté adjacent au côté parallèle au
premier, ce qui veut dire, entre le premier et le 14e ou
le 16e côté. L’angle est justement l’angle externe entre
deux côtés adjacents, qui est 12°.
36e SESSION DE
PERFECTIONNEMENT :
La mathématique, un parcours de choix
Cégep de Granby Haute-Yamaska, Granby
26 mai au 29 mai 2009
Visitez le site du GRMS pour plus de détails :
www.grms.qc.ca