dipole rc-cinétique chimique bac sc

Page 1
LYCEE ZAHROUNI
SERIE 7
Sciences physiques
OCTOBRE 2021
DIPOLE RC- CINETIQUE CHIMIQUE
Exercice 1
On dispose de deux béchers on introduit dans le 1er un volume V1= 25mL d’une solution (S1)
d’iodure de potassium de concentration molaire C1 et dans le 2éme un volume V2= 25mL d’une
solution acidifiée (S2) d’eau oxygéné de concentration molaire C2.
À la date t=0s, on mélange, en agitant, les contenus des deux béchers, la réaction totale qui se
produit est modélisée par l’équation :
Pour étudier la cinétique de cette réaction on réalise des prélèvements identiques de volume
VP=5mL chacun et on dose la quantité de diiode formé par une solution de thiosulfate de sodium
Na2S2O3 de concentration molaire C=0,5mol.L-1.
L’équation de la réaction de dosage rapide et totale est :
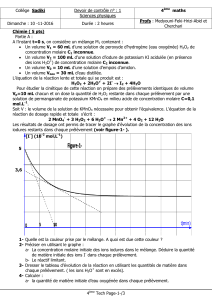
Les résultats du dosage ont permis de tracer la courbe traduisant la variation de n(H2O2) au cours du
temps figure 1
1°)
a- Donner la définition d’une réaction totale.
b- Quel autre caractère de la réaction étudiée
peut-on dégager à partir de la courbe.
2°)
a- Dresser le tableau d’avancement de la réaction
étudiée en utilisant les quantités de matière initiales
n0(I-) et n0(H2O2) dans chaque prélèvement.
b- Déterminer l’avancement final x
f et déduire n0(I-).
3°) Déterminer la concentration molaire de l’eau
oxygénée et celle des ions iodure dans le mélange à la
date t=0s. Déduire les valeurs des concentrations
molaires C1 et C2.
4°)
a- Définir le temps de demi-réaction . Déterminer sa valeur.
b- Déterminer le volume V de la solution de thiosulfate de sodium ajouté pour atteindre
l’équivalence à l’instant de date .
c- Si on réalise l’expérience en présence de quelques gouttes d’une solution contenant des ions
Fe2+, préciser, en justifiant, si ces affirmations sont vrais ou fausses
 le temps de demi-réaction ne varie pas.
 le volume V est supérieur à celui trouvé en b-).
5°) Tracer, en réalisant les calculs nécessaires, l’allure de la courbe d’évolution de n(H2O2) en
fonction du temps si on ajoute une masse m=3,32g d’iodure de potassium KI au mélange initial
sans changement de volume. On donne : masse molaire moléculaire MKI= 166 g.mol-1
-
2 2 3 2 2
H O + 2I 2H O I + 4H O
2- - 2-
2 2 3 4 6
I + 2S O 2I +S O
12
t
12
t
2
3
4
5
1
t(min)
n(H2O2) (10-3mol)
4
8
12
16
24
20

Page 2
Exercice 2
On réalise le montage schématisé ci-contre comportant :
 Un générateur idéal de tension maintenant entre ses bornes
une tension constante E
 Un générateur idéal de courant délivrant un courant
électrique d’intensité I0
 Un condensateur initialement déchargé de capacité C
 Trois conducteurs ohmiques de résistance respectives
R=2500Ω, R1 et R2 avec R1=R2
 Un commutateur K et un interrupteur K1 initialement ouverts.
I- A un instant t0 = 0, pris comme origine des temps, le
commutateur K est placé sur la position (1) et on
visualise, à l’aide d’un oscilloscope numérique utilisant la
même sensibilité pour les deux voies, la tension uMB(t)
aux bornes du condensateur (voie 1) et la tension uAB(t)
aux bornes de l’ensemble (résistor R, condensateur) (voie
2). On obtient les courbes uMB = f(t) et uAB = g(t) (Voir
figure 2)
1°) En utilisant les graphes de la figure 2
a-Etablir en fonction du temps l’expression des
tensions uMB(t) et uAB(t).
b-Déterminer la valeur de :
 L’intensité du courant I0 ;
 La capacité C du condensateur.
2°) A quel instant de date t1, uC = U1 = 2V.
II- À l’instant de date t1, pris comme nouveau
origine de temps, on ferme K1 et on bascule K de la
position (1) à la position (2).Un oscilloscope à mémoire
permet de visualiser, au cours du temps, l’évolution de
la tension uC aux bornes du condensateur. On obtient la
courbe représentée par la figure 3
1°)
a- Etablir l’équation différentielle vérifiée par uC(t).
b- La solution de cette équation différentielle s’écrit : uC(t) = A.eK.t + B.
Montrer que A = U1 – E ; B = E et K = -1/ 𝝉 où 𝜏 est la constante de temps du dipôle (RR2C).
c- Déterminer l’expression de uC à t = 𝝉.
2°) En exploitant la courbe de la figure 2, déterminer :
a- la valeur de E ;
b- la valeur de la constante de temps 𝝉 du dipôle (RR2C).. Trouver la valeur de R2
3°)
a- Déterminer l’expression de uR2(t).
b- Représenter, sur la figure 3 l’allure de la courbe qui traduit l’évolution de la tension uR2(t)
4°)
a- Déterminer, à 1‰ prés, la valeur de la durée t au bout de laquelle le condensateur devient
complètement chargé.
b- Déterminer l’énergie électrostatique emmagasinée par le condensateur à t >t
I0
(1)
(2)
(K)
R
C
A
B
E
K1
R1
R2
M
Figure 2
0 40 80 t(ms)
2
4
6
uC(V)
Figure 3