CCF Calcul numérique, repérage, proportionnalité

CERTIFICAT D'APTITUDE PROFESSIONNELLE
CCF Mathématiques : EXEMPLE
Calcul numérique, repérage, proportionnalité
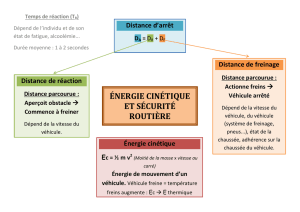
Un conducteur surpris par un événement imprévu ne modifie pas immédiatement la conduite de
son véhicule : il le fait toujours avec un temps de retard. Ce temps de retard s'appelle "temps de
réaction". Pendant ce temps, le véhicule parcourt à vitesse constante une certaine distance appelée
"distance de réaction". Ensuite, le conducteur appuie sur le frein : le véhicule parcourt alors la
"distance de freinage" jusqu'à l'arrêt complet.
I. Étude de la 1ère phase : la réaction
Dans cette partie, la vitesse reste constante et on peut utiliser la relation : d = v x t .
1. Un véhicule roule à la vitesse de 10 m/s : il parcourt ainsi une distance de 10 mètres en
1 seconde.
a) Calculer le nombre de secondes qu'il y a dans 1 heure.
b) Calculer la distance, en m, puis en km, parcourue par ce véhicule en 1 heure.
c) En déduire que la vitesse de 10 m/s correspond à la vitesse de 36 km/h.
2. Montrer que la vitesse de 90 km/h correspond à la vitesse de 25 m/s.
3. Le temps de réaction moyen d'un conducteur est t = 0,9 s.
a) Calculer la distance dR , en mètre, parcourue pendant ce temps de réaction moyen
par un véhicule roulant à la vitesse constante de 10 m/s.
b) Calculer la distance dR , en mètre, au dixième, parcourue pendant ce même temps de
réaction moyen par un véhicule roulant à la vitesse constante de 90 km/h.

4. Pour un temps de réaction moyen de 0,9 s, on a établi le tableau de valeurs suivant :
Vitesse du véhicule
en km/h
18
54
72
108
Vitesse v du véhicule
en m/s
5
15
20
30
Distance dR de réaction
en m
4,5
13,5
18
27
a) Placer dans le repère ci-dessous les points dont les coordonnées (v ; dR)
correspondent aux valeurs du tableau.
Distance de réaction dR (m)
30
20
10
0 10 20 30 vitesse v
(m/s)
b) On sait qu'une situation de proportionnalité est représentée graphiquement par des
points situés sur une demi-droite issue de l'origine des axes.
Dire, en justifiant la réponse, si votre représentation graphique indique que la
distance de réaction dR est proportionnelle à la vitesse v du véhicule.

II. Étude de la 2ème phase : le freinage
La distance de freinage d'un véhicule dépend de sa vitesse et de l'état de la route.
Dans le repère ci-dessous, la courbe  représente la distance de freinage d'un véhicule en
fonction de sa vitesse sur route sèche et la courbe  sur route humide.
Distance de freinage (m)
10 50 100 Vitesse (km/h)
1. Dire, en justifiant la réponse, si la distance de freinage d'un véhicule sur route humide
est proportionnelle à sa vitesse.
2. A l'aide de ces représentations graphiques, indiquer :
a) La distance de freinage, en m, d'un véhicule roulant à 90 km/h sur route sèche.
b) La distance de freinage, en m, d'un véhicule roulant à 90 km/h sur route humide.
c) La vitesse, en km/h, d'un véhicule qui, sur route humide, freine sur 100 m.
III. Étude d'un exemple complet
Un conducteur, roulant sur une route sèche à la vitesse stabilisée de 90 km/h, aperçoit
soudain un obstacle à 100 m devant son véhicule.
1. A l'aide des résultats précédents, indiquer :
a) sa vitesse, en m/s.
b) le temps de réaction moyen, en s.
c) la distance, en m, parcourue par le véhicule pendant ce temps de réaction moyen.
d) la distance de freinage, en m.
e) la distance d'arrêt totale, en m.
2. Conclure : le conducteur pourra-t-il arrêter son véhicule à temps ?
50
100
150
0