DEUX CONDENSATEURS FONT LA COURSE

DEUX CONDENSATEURS FONT LA COURSE
A. Les conditions de charge sont identiques (E = 5V et R1 = R2)
On veut comparer les temps de charge de
deux condensateurs de capacités
C1 = 1 mF et C2 = 2 mF.
I. Etude théorique
1. Pour un circuit RC série, donner la relation liant la tension Ur(t) à l’intensité i(t) puis celle
liant Uc(t) à la charge q(t).
2. Donner la relation liant l’intensité i(t) à la charge q(t) et en déduire celle liant Ur(t) et
Uc(t).
3. En déduire, dans un circuit RC alimenté par la tension E, l’équation différentielle vérifiée
par la tension Uc(t).
4. Vérifier que l’expression Uc(t) = E(1-et/τ) est solution de cette équation.
5. Que représente la grandeur τ, donner son expression et son unité.
II. Course à la charge
A l’instant t = 0, on ferme simultanément les deux interrupteurs.
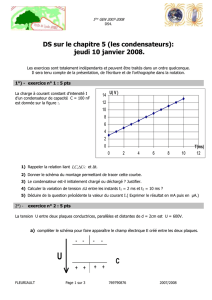
Sur l’annexe figure l’enregistrement de la tension U1(t) aux bornes du condensateur C1.
1. Déterminer, par la méthode de votre choix, la constante de temps τ1 de la branche 1.
2. En déduire la valeur de la résistance R1, puis celle de R2.
3. Calculer la constante de temps τ2 de la branche 2.
4. Tracer sur le graphique, l’évolution de la tension U2(t) aux bornes du condensateur C2.
5. Justifier quel condensateur sera le premier chargé ?
6. Calculer les énergies stockées dans les condensateurs C1 et C2 lorsque le régime
permanent sera atteint.
III. Course à la décharge
A la date t = 2s, on amène le générateur à 0V, celui-ci est alors équivalent à un fil.
1. Représenter sur le schéma précédent l’évolution des tensions U1(t) et U2(t).
2. Déterminer graphiquement la date à laquelle les tensions U1 et U2 sont égales.
3. Justifier quel condensateur sera le premier déchargé ?

B. Les conditions de charge diffèrent (E1 = 5 V, R1 = 1 k et E2  E1, R2’  R1)
On veut maintenant charger les
deux condensateurs de capacités
C1 = 1 mF et C2 = 2 mF de la
même énergie dans le même
temps.
K1 et K2 fonctionnent
simultanément et K reste ouvert
dans la première partie.
I. Charges simultanées
Sur l’annexe figure l’enregistrement de la tension U1(t) aux bornes du condensateur C1.
1. Quelle est la constante de temps τ1 dans la branche 1 ?
2. En déduire la valeur de la résistance R2’ pour obtenir la même durée de charge pour le
condensateur C2.
3. Quelle sera l’énergie stockée dans le condensateur C1 ?
4. En déduire la valeur de la tension E2 pour obtenir la même énergie stockée dans le
condensateur C2.
5. Tracer sur le graphique, l’évolution de la tension U2(t) aux bornes du condensateur C2.
6. Quelle durée minimale faut-il attendre pour que les régimes permanents soient atteints ?
II. Connexion des circuits
Les régimes permanents étant atteints, on ouvre les interrupteurs K1 et K2 puis on ferme
l’interrupteur K.
1. Quel sera le sens du courant dans le circuit formé ?
2. Quelle(s) grandeur(s) parmi : intensité, tension, charge, énergie, sera(seront) commune(s)
aux deux condensateurs lorsque le nouveau régime permanant sera atteint ?
3. Sachant que les énergies et les capacités s’ajoutent, déterminer la tension finale aux
bornes des condensateurs.

ANNEXES
A. Les conditions de charge sont identiques
B. Les conditions de charge diffèrent