ex 2, 3 et 5, PII

EXERCICES du chap PII
Données :
1al = 9,5.1015m
c = 3,0.108m.s-1
Exercice 1
L’étoile polaire se situe à 4,3.106 milliards de km de la terre. Convertir cette distance en
années lumières.
Exercice 2
L’étoile Eta Carina est à presque 7,500.103 al de la terre. Convertir cette distance en m puis
en km.
Exercice 3
Le soleil est à 1,50.102 millions de km de la terre. Déterminer la durée mise par la lumière du
soleil pour nous parvenir.
Exercice 4
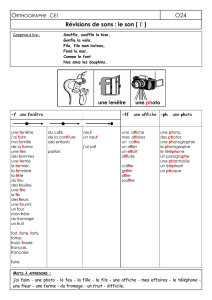
A travers une fenêtre, Antoine observe un
arbre qui se situe en face de sa maison. Il
recule jusqu’à ce que l’arbre ait la même
hauteur apparente que la fenêtre.
Il repère sa position et mesure, avec un
mètre, la distance d qui le sépare de la
fenêtre (d = 3,36m) puis la hauteur h de la
fenêtre (h=1,16m). Enfin, avec un décamètre, il mesure la distance D entre la fenêtre et
l’arbre (D=1,27.101m).
1) Schématiser la situation en utilisant un ou plusieurs triangles.
2) Déterminer la hauteur H de l’arbre en mètres.
3) Justifier le nombre de chiffres significatifs de votre résultats.
Exercice 5
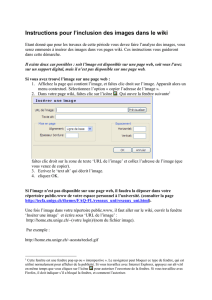
Zoé voyage à Paris et admire la tour Eiffel.
Elle souhaite estimer sa hauteur h. Pour cela,
elle prend la règle et la tient verticalement
bras tendu et vise la tour. La règle est à une
distance
l’= 6,0.101cm de son œil. En alignant le zéro de
la règle avec le pied de la tour, elle constate
que le sommet s’aligne avec la graduation h’ =
3,49.101cm. Elle se trouve à l = 5,5.10-1km de la tour Eiffel.
1) Convertir toutes les longueurs en m.
2) Schématiser la situation en utilisant un ou plusieurs triangles.
3) Déterminer la hauteur h de la tour Eiffel.
4) Justifier le nombre de chiffres significatifs de votre résultats
EXERCICES du chap PII
Données :
1al = 9,5.1015m
c = 3,0.108m.s-1
Exercice 1
L’étoile polaire se situe à 4,3.106 milliards de km de la terre. Convertir cette distance en
années lumières.
Exercice 2
L’étoile Eta Carina est à presque 7,500.103 al de la terre. Convertir cette distance en m puis
en km.
Exercice 3
Le soleil est à 1,50.102 millions de km de la terre. Déterminer la durée mise par la lumière du
soleil pour nous parvenir.
Exercice 4
A travers une fenêtre, Antoine observe un
arbre qui se situe en face de sa maison. Il
recule jusqu’à ce que l’arbre ait la même
hauteur apparente que la fenêtre.
Il repère sa position et mesure, avec un
mètre, la distance d qui le sépare de la
fenêtre (d = 3,36m) puis la hauteur h de la
fenêtre (h=1,16m). Enfin, avec un décamètre, il mesure la distance D entre la fenêtre et
l’arbre (D=1,27.101m).
4) Schématiser la situation en utilisant un ou plusieurs triangles.
5) Déterminer la hauteur H de l’arbre en mètres.
6) Justifier le nombre de chiffres significatifs de votre résultats.
Exercice 5
Zoé voyage à Paris et admire la tour Eiffel.
Elle souhaite estimer sa hauteur h. Pour cela,
elle prend la règle et la tient verticalement
bras tendu et vise la tour. La règle est à une
distance
l’= 6,0.101cm de son œil. En alignant le zéro de
la règle avec le pied de la tour, elle constate
que le sommet s’aligne avec la graduation h’ =
3,49.101cm. Elle se trouve à l = 5,5.10-1km de la tour Eiffel.
5) Convertir toutes les longueurs en m.
6) Schématiser la situation en utilisant un ou plusieurs triangles.
7) Déterminer la hauteur h de la tour Eiffel.
8) Justifier le nombre de chiffres significatifs de votre résultats