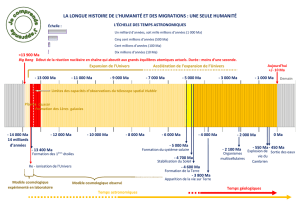
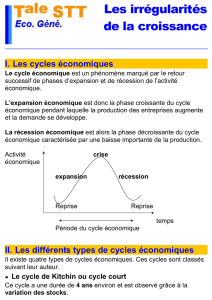
pression du milieu cosmique

PRESSION DU MILIEU COSMIQUE
CONSEQUENCES
Philippe Magne
Mars 2004

Introduction
Habituellement, la pression est définie comme une densité superficielle de force, ce qui
permet de calculer la force qui s’exercerait sur une paroi plane de surface connue.
Ajoutons que cette force ne peut exister que si la pression est plus grande d’un côté de la paroi
que de l’autre.
Dans l’univers uniforme, tous les endroits sont pareils et la pression est la même partout, il
n’y a pas de gradient de pression, aucune force comme celle évoquée ci-dessus ne peut se
manifester.
Alors, on peut se poser la question : comment la pression peut-elle affecter l’expansion ?
Pour répondre, il faut prendre conscience que la pression est une forme de l’énergie, laquelle
comme toutes les autres énergies, est source de gravitation à cause de l’équivalence masse
énergie exprimée par la célèbre formule E = m c²
Traduite dans le langage de la Relativité Générale, la pression contribue à courber l’espace-
temps comme le fait la présence de la matière.
D’une façon très simple on peut montrer le caractère énergétique de la pression P par
l’analyse dimensionnelle suivante :
Classiquement
2
Force F
PSurface L
( 1 )
Si l’on multiplie le numérateur et le dénominateur de cette fraction par une longueur L , on ne
change pas la dimension de P, on aboutit à :
23
F L F L Energie
PL Volume
LL
densité d’énergie ( 2 )
Champ de gravitation et Pression, conséquences
D’une manière générale le champ de gravitation peut s’écrire :
2
GM
RR
( 3 ) formule qui exprime une accélération négative
11
6.62 10G CUG 
M
= masse en kg
R
distance au centre de gravité en mètres
Si l’on considère un volume sphérique de rayon R la masse M est égale au produit de ce
volume par la densité . Etant donnée l’équivalence masse énergie il faut grever la densité de
la pression P convertie en masse
²
P
c

Plus exactement de
3² P
c
parce que le milieu est isotope et homogène, la pression existe dans
les 3 dimensions de l’espace ( équipartition de l’énergie )
3
43
3²
P
MR c
( 4 )
Pour alléger l’écriture faisons
1c
, le champ de gravitation s’écrit alors :
3
2
4( 3 )
3GR
RP
R
( 5 )
Voyons maintenant comment on peut mettre en évidence la contribution de la pression à la
dynamique de l’expansion. Pour cela il faut établir une relation où interviennent à la fois la
pression et la constante de Hubble.
On part de l’équation de Friedmann :
3
24
1²
3
22
GR kc
RR
( 6 )
Différentions cette équation par rapport au temps :
2
420
3Gd
RR R RR
dt
( 7 )
Bien noter que est une fonction du temps au même titre que R ( facteur d’échelle en
l’occurrence )
Portons l’expression de
R
( 5 ) dans cette expression, il vient :
2
44
( 3 ) 2 0
33
G G d
RR P R RR
dt
( 8 )
D’où l’on tire :
2
33
d
RR R PRR
dt
( 9 )
En multipliant par
R
les deux membre de cette dernière équation on aboutit à :
2 3 2
33
d
R R R PR R
dt
( 10 )

On aura reconnu dans cette expression les dérivées ci- dessous :
33
( ) ( )d R d R
P
dt dt
( 11 )
3
()dR
est une variation différentielle d’énergie en raison de l’équivalence masse énergie
3
()dR
a la forme d’une variation différentielle de volume
On retrouve ainsi l’équation d’état classique :
dE PdV
( dans la condition adiabatique ) ( 12 )
Dans la phase actuelle de l’expansion on peut admettre que la pression est nulle, mais il n’en
fut pas toujours ainsi comme nous le verrons plus loin.
Si la pression est nulle on a :
3
()
0
dR
dt
( 13 )
Ce qui exprime la conservation de la masse, d’où l’égalité
33
00
RR
= Cte , l’indice 0
signifiant que les paramètres sont pris au temps présent
0
t
Revenons maintenant à l’expression générale ( 10 ) pour introduire la constante de Hubble
2 3 2
33
d
R R R PR R
dt
( 14 )
Divisons tous les termes par
3
R
33
R d R
P
R dt R
( 15 )
RH
R
constante de Hubble ( constante partout dans l’espace, mais pas dans le temps )
Il vient alors
3 ( )
dHP
dt
( 16 )

Phases de l’expansion de l’univers
Trois sortes d’énergies interviennent par leur équivalent massique.
Par ordre d’entrée en « scène » :
 Le rayonnement électromagnétique ( EM ) du corps noir cosmologique à très haute
température à partir duquel se formèrent toutes les particules pendant son
refroidissement.
Ce rayonnement est encore perçu aujourd’hui comme bruit cosmique que l’on appelle
aussi Fond Diffus Cosmologique ( FDC ) ou Cosmic Microwave Background ( CMB )
Sa température a été mesurée avec précision, elle est de 2.725 K
 La matiére sous toute ses formes, noire non baryonique, noire baryonique et lumineuse
baryonique ( galaxies et étoiles )
 La quintessence ou énergie noire répulsive du vide découverte récemment ( de façon
indirecte ) en constatant que l’expansion s’accélère.
Nous verrons que cette composante a la particularité d’avoir une pression négative.
C’est une notion un peu difficile à comprendre, elle a le sens d’une contrainte en
expansion, la pression peut s’annuler bien que la densité ne soit pas nulle, ce qui peut
mettre sur la voie de son adoption.
Pression dans la phase où l’EM gouverne l’expansion
Pour mieux analyser son rôle on se place dans la condition où elle supplante les deux autres
énergies, c’est à dire lorsque l’univers primordial est uniquement composé de radiations EM,
les particules de matière naissante sont ultra relativistes et se comportent comme des photons,
on assimile le milieu à un gaz de photons.
Voyons maintenant en quoi la vitesse des particules intervient.
Dans un gaz, la vitesse du son est donnée grossièrement par la formule approximative :
1
2
P
v
est la densité du gaz ( 17 )
Nous pouvons aussi écrire cette équation en divisant les deux membres par la vitesse de la
lumière c
1
2
²
vP
cc
avec
2
c
densité d’énergie du gaz de photons ( 18 )