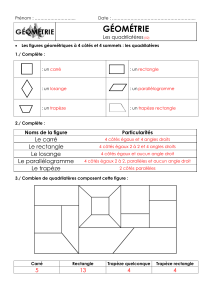
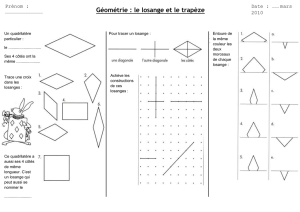
Suite de notre recherche du problème babylonien - 6a

- Suite de notre recherche du problème babylonien - 6a - Providence -
On est allés sur le site pour chercher des idées et on a lu les recherches de Thuir et de Lodève
 Nous en sommes là !
- Après une recherche historique pour plus d’informations sur Babylone / Mésopotamie grâce au
professeur d’histoire ( Pourquoi à cette époque les champs avaient-ils la forme de trapèze ? )
- Le professeur de technologie nous a apporté une chaîne d’arpenteur et des photocopies de
renseignements sur les méthodes de mesurage des arpenteurs, et les cordes à nœuds.
- Recherche de définitions sur des dictionnaires et sur des livres de Math : Partage équitable /
trapèze / formule d’aire…
- Le professeur de français a expliqué le sens du verbe « arpenter » dans l’expression trouvée
dans un livre qu’un élève était en train de lire : « des gens arpentaient les boulevards….. »
 Questions autour de :
- L’absence d’unités de mesure avec 7 et 17, après discussion, ce n’est pas l’auteur qui les a
oubliées, c’était inutile comme information !
- On n’arrive pas à savoir si c’est important que 7 et 17 se terminent par 7 ;
- On est gêné de ne pas avoir d’informations sur la hauteur du trapèze et sur la longueur des
côtés non parallèles, surtout pour faire les dessins ;
- Sur le dessin du problème, les côtés parallèles ne mesurent pas 7 et 17 cm.
 Procédures par construction sur papier quadrillé du champ avec 7 et 17 cm
- Tâtonnement par essais / erreurs – Découpage et recollage .
- Construction – positionnement divers de la largeur du milieu et à chaque fois dénombrement du
nombre de carreaux avec évaluation « des morceaux de carreaux »,qu’on assemble par collage ;
- Comment calculer l’aire d’un trapèze ? Et si on rabattait vers l’intérieur, les triangles qui sont sur
les côtés ?
 Etudes sur des cas particuliers de figures :
- Avec côtés obliques perpendiculaires aux bases ( les deux c’est pas possible ! )
- Avec côtés obliques égaux ;
- Avec axe de symétrie vertical ( c’est pas le problème ), ou horizontal ( c’est pas équitable )
 Conjecture autour de la mesure « logique » de cette largeur du milieu :
- Si le trait de la « largeur milieu » était vertical, le problème serait plus facile ;
- Le nombre cherché est obligatoirement compris entre 7 et 17 ;
- Affirmations proposées sur la largeur du milieu : 12 ( avec calcul ) / 13 ( sans explication) /
environ 13 / 13,2 … 10,56 avec calculs du type « âge du capitaine » /
- Premier raisonnement : C’est obligé qu’il faut couper plus haut que le milieu, 12 c’est pas bon
pour la largeur du milieu, parce que les deux morceaux sont pas égaux, il faut se rapprocher du
plus grand, de 17 , donc ce doit être plus de 12 , alors peut être 13 , ou entre 12 et 13 ?
 Formule de l’aire d’un trapèze proposée dans plusieurs écrits :
- Chaque champ se retrouve à présent avec la donnée suivante ; l’aire de chaque parcelle doit
être égale à 6h , avec h qui correspond à la hauteur du trapèze.
 On est en train de faire des essais de calculs avec cette formule d’aire, en prenant des
valeurs simples pour h, la hauteur du trapèze……
( 29/09/04 ) A bientôt