Sciences Physique

1
Sciences Physiques 2010 - S. Zayyani
Fiche de Cours
Unité : L’univers
Chapitre: 1 – Présentation de l’univers
L’Univers
Les trois échelles
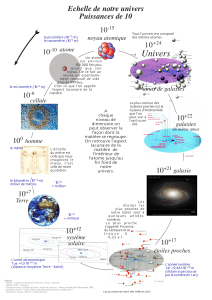
On peut classifier l’univers autour de nous selon trois échelles (scale) de taille :
i. Echelle atomique (ou microscopique)
ii. Echelle humaine
iii. Echelle astronomique (ou cosmique)
L’échelle atomique
Prenons l’exemple d’un atome d’hydrogène. (Quels sont les composants de cet atome ?)
Un atome d’hydrogène contient un seul électron en orbite autour du
noyau. est le diamètre du noyau, et est le diamètre de
l’atome. Les deux grandeurs sont de l’ordre de grandeur (en km) :
Calculons le rapport (ratio) de ces deux dimensions :
C’est-à-dire, le diamètre d’un atome d’hydrogène est 10 milles fois
plus grande que le noyau. (Pour visualiser ce rapport, si un atome
avait la taille du Stade de France, son noyau aurait environ la taille d’une tête d’épingle !)
Et, qu’est-ce qu’il y entre le noyau d’atome et sa couche électronique ? Rien ! Ou plus précisément, du vide.
Calculez le pourcentage du volume de cet atome qui est vide.
On voit que (selon le calcul ci-dessus) qu’en effet, un atome se compose entièrement (presque) du
vide. (Encore pour visualiser cela : La Terre est une sphère avec un rayon de 6500000 m. Si on supprimait le
vide intérieur de tous les atomes constituant la Terre, on pourrait les rassembler dans une boule de 150 m.)
Petit
Grand

2
Pour cette raison on dit que l’atome a une structure Lacunaire. (lacune = gap)
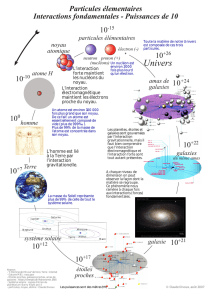
L’échelle astronomique
En général, concernant la distribution de la matière dans l’univers, on parle des régions de basse-densité (là où
il n’y a que du vide), et les régions de haute-densité (là où existent les galaxies et des nébuleuses. Prenons
maintenant le cas de la Terre dans le système solaire. Dans le système solaire, le Soleil et les planètes
occupent des volumes de matière extrêmement petits.
Question : Sachant que le rayon solaire est de    ; Rayon terrestre est de    ;
et Rayon d’orbite de la Terre est de , calculez le pourcentage du volume
d’espace entre la Terre et le soleil qui est vide. (Volume d’une sphère 
)
On voit, qu’en fait l’espace est presque totalement vide aussi. Le même vide existe entre les étoiles dans une
galaxie, et entre les galaxies eux-mêmes. Donc on voit que le remplissage de l’espace, à l’échelle
astronomique a une structure lacunaire.

3
La Lumière
On a appris en collège que la propagation de la lumière est rectiligne. Mais qu’est-ce que ça veut dire ?
Ça veut dire, la lumière se propage en ligne droite.
Mais maintenant on peut approfondir ce modèle de la lumière. D’abord on peut classifier les milieux traversés
par la lumière :
- Milieu transparent et homogène
- Milieu transparent et hétérogène
- Milieu opaque
Déjà, on peut définir un milieu (=medium) opaque comme un milieu qui ne permet pas la propagation de la
lumière. Donc la lumière se propage seulement dans les milieux transparents.
DÉFINITION : Un milieu homogène possède les mêmes propriétés physique et chimique en
chacun de ses points (eg. Air avec la même température, pression et
concentration partout). Donc un milieu homogène est un milieu dont les points
ne possèdent pas les mêmes propriétés (eg. Air chauffé).
Donc on peut améliorer maintenant notre modèle de la propagation de la lumière :
Dans le vide (=vaccuum) et dans tout milieu homogène et transparent la lumière se
propage en ligne droite (i.e. rectiligne). On modélise le trajet de la lumière entre
deux points par des segments de droite orientés dans le sens de la propagation. Ces
segments sont appelés Rayons Lumineux (= rays of lights, light rays).
Depuis les travaux de Michelson, Morley et Einstein on postule que la vitesse de la lumière dans le vide, notée
c, est une constante universelle, indépendant du référentiel dans lequel on la mesure (on rencontra cette
notion en Mécanique).
Question : Proposer quelques méthodes pour mesurer cette vitesse. Est-il possible de la faire sans faire
refléter les rayons lumineux ?
Selon la théorie d’Einstein, la vitesse de la lumière est la vitesse limite dans notre univers(=universe).
Année de Lumière
Mettons-nous à l’échelle astronomique. Voici quelques distances – assez courtes – à cette échelle :
- Soleil – Terre :  
- Soleil – Pluton :   (Pluton n’est plus une planète :< )
- Soleil – étoile la plus proche :   (l’étoile la plus proche = Proxima de Centaure)
- Soleil – Galaxie la plus proche :   (galaxie la plus proche = Andromède)

4
Evidemment, le choix du kilomètre n’est pas vraiment pratique pour distance de cette échelle (on ne mesurait
pas la distance Paris-Lyon en millimètre).
Donc on a besoin d’introduire une nouvelle unité de distance qui est plus adaptée à cette échelle. Une
première unité ‘astronomique’ est … l’Unité Astronomique !
Donc un objet à une distance de 10 u.a. est 10 fois plus loin que le soleil.
Mais, cette unité est toujours trop petite quand il s’agit des distances entres les galaxies ou quand il s’agit de
la taille de l’univers visible. Pour ces dernières on introduit une autre unité basée sur la vitesse de la lumière :
l’année de lumière (a.l.)(=Light Year).
DEFINITION: L’année de lumière est la distance parcourue par la lumière pendant un an dans le vide (donc à
une vitesse de     .     
Question : comment calculer cette distance ?
Solution : On se rappelle que la distance parcourue est liée à la vitesse grâce à la relation :
La vitesse est connue (la vitesse de la lumière, c), et le temps du parcours = un an. Mais d’abord il faut
convertir en secondes :
EXEMPLE : Donner les distances ci-dessus d’abord en UA, et puis en a.l.
Solution : Terre-Andromède :       
Terre-soleil :
Pluton-soleil :

5
Question : Pourquoi utilise-t-on une unité bizarre comme l’année de lumière au lieu d’une unité ‘plus
logique’ de base de 10 (comme Teramètre par exemple) ?
Réponse : La réponse simple : car c’est la convention, c’est tout. Mais ce n’est pas forcement le cas.
En fait selon la théorie d’Einstein, cette vitesse maximum est la vitesse max de transmission
d’information aussi, ainsi que la vitesse de passage du temps !!!
Donc en établissant une unité de longueur basée sur la vitesse de la lumière on établit une relation entre
distance et temps.
La clé est le fait que la vitesse de la lumière n’est pas infinie ! Cela veut dire que, la lumière d’une étoile située
à une distance de 2 a.l. , a besoin de 2 ans afin de nous parvenir (en fait non seulement la lumière mais toute
information sur cette étoile). Donc la lumière, ou notre image de cette étoile, est l’image de cet objet dans le
passé ; d’il y a deux ans !
D’où vient « Voir loin, c’est voir dans le passé ».
Cela est vrai pour tout objets que l’on voit, mêmes les objets à quelques mètre ou centimètre. La seule
différence étant le temps du parcours. Pour les objets terrestres, l’intervalle est tellement petit que l’on ne
peut pas l’apercevoir, et donc c’est en pratique instantané.
Maintenant, on peut calculer « la distance dans le passé » pour les objets précédents.
Soleil – Terre : 8 minutes
Soleil – Pluton : 6 heures
Soleil – Proxima : 4 ans
Soleil – Andromède : 1 million ans
(Conséquence ? Si le soleil s’explose, on ne va pas savoir avant 8 minutes. On va le voir comme d’habitude
jusqu’à 8 minutes après son explosion en réalité ! )
De plus, le plus loin que l’on regarde, le plus loin dans le passé, et donc le plus proche au moment de création
de notre univers. Pour le moments les objets le plus loin observes sont des Quasars, qui se trouvent à une
distance d’environ 12 – 15 milliards a.l. , c'est-à-dire on les voit comme ils étaient il y 12 – 15 milliard ans !)