Ae 5 effet doppler avec correction

Terminale S
AE 5_L’effet Doppler
M.Meyniel 1/5
Échelle de fréquence des sons
L’EFFET DOPPLER-FIZEAU
Objectifs : - Découvrir l’effet Doppler et le mettre en œuvre pour mesurer une vitesse.
- Réaliser une démarche expérimentale en utilisant de nouveau les logiciels de traitement de signaux.
Document 0 : L’effet Doppler-Fizeau
Changement apparent de la fréquence d'un signal […] reçu par un observateur mobile par rapport à une
source émettrice fixe ou bien par un observateur fixe par rapport à une source émettrice mobile. La variation
apparente de fréquence Δf est proportionnelle à la vitesse v relative entre l’observateur et la source le long du
chemin qui les sépare. L’effet Doppler est utilisé en astrophysique pour connaître la vitesse angulaire des étoiles car
leur mouvement, selon la perspective, provoque un déplacement des raies émises par rapport aux mêmes raies
émises par une source terrestre.
Le son émis par un mobile en mouvement semble plus ou moins aigu selon la vitesse à laquelle il se rapproche, et
plus ou moins grave selon la vitesse à laquelle il s'éloigne.
On détermine ainsi la vitesse d'un mobile émettant du son ou de la lumière, en mesurant le décalage de la
fréquence reçue par rapport à la fréquence émise.
On peut montrer que l’expression (à ne pas connaître) du décalage Doppler est : 
Avec VS : la vitesse de la source.
c : célérité de l’onde (pour le son dans l’air à 20°C : cSON = 340 m.s-1 ; pour la lumière : c = 3,0.108 m.s-1)
f1 et f2 : fréquence (en Hz) reçue lorsque la source se rapproche et lorsqu’elle s’éloigne.
D’après www.futura-sciences.com
Ici, nous allons chercher à mesurer la vitesse d’une voiture ainsi que celle d’une étoile.
I. Vitesse de la moto.
On dispose d’un fichier sonore d’une moto se déplaçant sur une route à une vitesse VS.
Problématique :
Le motocycliste est-il en infraction ?
Pour répondre à cette question, on pourra utiliser le logiciel Audacity®.
Vous proposerez pour cela un protocole détaillé (que vous présenterez à votre professeur), puis réaliserez
vos mesures pour enfin répondre à la problématique posée.
Sur votre compte-rendu, décrire précisément la description de la démarche expérimentale, les résultats
obtenus (reproduction des spectres en fréquence) et votre conclusion.
t (s)
U (V)
La moto s’approche… …………passe devant l’observateur……………… puis s’éloigne.
Zones à étudier
Repères sur le signal
Extrait sonore du son perçu par l’observateur

Terminale S
AE 5_L’effet Doppler
M.Meyniel 2/5
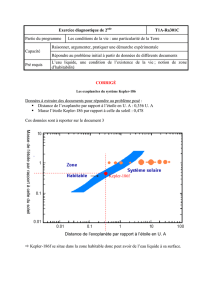
II. Détection d’exoplanètes.
Il est exceptionnel de détecter visuellement des exoplanètes à cause de la forte luminosité des étoiles
comparée à celle des planètes. De plus, à cause leur éloignement, la plupart des étoiles sont réduites à un
point lumineux, même avec un télescope puissant. Malgré tout, un millier d’exoplanètes a pu être détecté
par diverses méthodes comme la méthode des « vitesses radiales » qui utilise l’effet Doppler.
Le but de cette partie est de déterminer, dans un premier temps, la vitesse v (radiale) de l’étoile pour en
déduire dans un second temps, la période T de révolution de la planète ainsi que la masse M de l’étoile à
l’aide d’une des lois de Kepler (notion vue plus tard).
Document 1 : Décalage spectral
En appliquant l’effet Doppler sonore à la lumière, Christian Doppler (1803-1853), mathématicien et
physicien autrichien, suggère que la couleur des étoiles est une conséquence de leur mouvement par rapport à la
Terre. Le physicien et astronome français Hippolyte Fizeau (1819-1896) démontre en 1848 que la vitesse des étoiles
est trop faible par rapport à celle de la lumière pour que cet effet soit observable. Il conclut cependant que les raies
d’absorption d’un élément chimique sur le spectre d’une étoile en mouvement par rapport à la Terre doivent être
décalées par rapport à leur position sur le spectre du soleil. La mesure de ce décalage permettrait alors à remonter à
la vitesse de l’étoile dans la direction de l’observation : c’est la vitesse radiale.
Document 2 : Principe de la mesure
Cette prévision est confirmée en 1868 par l’astronome britannique William Huggins (1824-1910), qui
montre, en mesurant le décalage des raies de l’hydrogène, que l’étoile Sirius s’éloigne de la Terre à une vitesse de
46 km.s-1.
L’effet Doppler-Fizeau s’est plus récemment illustré dans la détection des exoplanètes, les planètes hors du
système solaire. En effet, le déplacement des raies sombres dans le spectre de l’étoile prouve la présence d’une
exoplanète massive autour de l’étoile.
La détermination de la vitesse radiale par le décalage Doppler permet de tracer la courbe de vitesse radiale
et ainsi de déterminer la présence d’une grosse planète ainsi que sa période de révolution.
Le décalage Doppler-Fizeau en longueur d’onde est donné par la relation : 
avec : Δλ = λ’-λ0 λ0 : longueur d’onde d’une raie de référence (dans le spectre du sodium) dans le spectre de raie
d’absorption d’une étoile fixe (Soleil),
λ' : longueur d’onde de la raie de référence dans le spectre de raie d’absorption d’une étoile mobile,
v : vitesse radiale de l’étoile par rapport à un observateur sur Terre,
c : célérité de la lumière dans le vide.

Terminale S
AE 5_L’effet Doppler
M.Meyniel 3/5
Pour bien comprendre le principe, rendez-vous sur le site : http://www.jf-noblet.fr/doppler/tp213.htm
1. Préciser l’origine des raies noires dans le spectre d’une étoile.
 Se connecter sur :
http://espacelycee.editions-bordas.fr/enseignant/anim/partie_1_sequence_4_activite_6_effet_doppler_fizeau
 Choisir le module « détection des exoplanètes », lire les informations données et cliquer sur « Application ».
On considère la planète 51 Pegasi b
 Déplacer le curseur pour déterminer avec précision la longueur d’onde
0 dans le spectre d’absorption du Soleil.
 Ensuite, sélectionner chaque spectre d’absorption de l’étoile et repérer la longueur d’onde ’ de la raie.
2. Proposer un protocole expérimental permettant de calculer la valeur de la vitesse (radiale) de l’étoile
pour tracer ensuite l’évolution de la vitesse (radiale) de l’étoile en fonction du temps (nombre de
jour) : « v = f (t) ». On pourra utiliser la fonction tableur du logiciel Latis-Pro®.
3. Commenter et interpréter l’allure de la courbe « v = f (t) ».
4. A partir de la courbe obtenue précédemment, déterminer approximativement la période de révolution
T de la planète.
5. La troisième loi de Kepler indique la relation suivante : 
avec : T : la période de révolution de la planète en seconde (s) ;
R : la distance étoile-planète en mètre (m) ;
G : la constante gravitationnelle : G = 6,67.10-11 USI ;
M : la masse de l’étoile en kilogramme (kg).
Sachant que le rayon de rotation de l’étoile avoisine les 590.106 m, en déduire la masse M de l’étoile.
Curseur déplaçable
λ
0
Spectre n°1
λ
Copie d’écran
légendée

Terminale S
AE 5_L’effet Doppler
M.Meyniel 4/5
Compte-rendu de l’effet Doppler
I. Comment mesurer de la vitesse d’une moto ?
Protocole expérimental :
 Ouverture de l’enregistrement sonore moto avec le logiciel Régavi.
 On sélectionne le début de l’enregistrement (avant le repère indiqué) et l’on transfert vers le logiciel Régressi la sélection.
 En cliquant sur l’onglet Fourier, on fait apparaître le spectre en fréquence correspondant.
 On utilise le réticule (icône Curseur) afin de déterminer la fréquence fondamentale f1 du signal. Un zoom (icône loupe)
amène plus de précision sur la mesure.
 On procède de la même façon avec la fin de l’enregistrement afin d’obtenir la fréquence f2.
Résultats et exploitation :
Les valeurs trouvées sont : f1 = 236 Hz & f2 = 210 Hz
La formule (3) permet d’obtenir la vitesse de la moto dans un
référentiel terrestre fixe :
Conclusion : Le motard respecte la limitation de vitesse puisque sa vitesse est inférieure à 90 km/h, la
limite imposée.
Rq : * Bien prendre un court intervalle de temps en début et fin pour être plus précis car on considère un grand intervalle de
temps entre le début et la fin ce qui amène plus de précision.
* Les sons ne sont pas purs puisque les enregistrements sont non sinusoïdaux et les spectres en fréquences présentent
plusieurs harmoniques.
II. Comment mesurer la vitesse radiale d’une étoile ?
1. Les raies noires proviennent des radiations absorbées par les gaz présents sur le trajet de la lumière =>
atmosphère de l’étoile et/ou de la Terre.
2.  Compléter le tableau avec les valeurs lues puis, avec l’aide des fonctions du tableur, calculer  = ’ -
0
 Toujours en utilisant les fonctionnalités du tableur,
calculer la vitesse radiale de l’étoile v en s’appuyant sur
la formule donnée dans le document 2. (La vitesse
radiale d’un objet est la composante de sa vitesse qui est
mesurée dans la direction de la ligne de visée de
l’observateur.)
Tableau de valeur :
 Tracer à l’aide du logiciel la courbe :
v = f (t) avec la vitesse en ordonnées
et le temps en abscisses
Graphique v = f (t) :
f
amplitude (mV)
f1 = 236 Hz
708 Hz
472 Hz

Terminale S
AE 5_L’effet Doppler
M.Meyniel 5/5
3. On retrouve une courbe sinusoïdale comme le mettait en avant la démonstration sur le site sous-entendant que
l’étoile se rapproche puis s’éloigne périodiquement de la Terre.
 Une exoplanète doit donc graviter autour d’elle-même !!!
4. Pour trouver la période de révolution :
- soit on utilise l’outil réticule pour déterminer la durée d’un motif : T = 365,764.103 s ;
- soit on regarde la modélisation de la courbe qui donne la fréquence :
modélisation : v(t) = 0.195 + 59.891 × sin(2 2.734-6 t + 1.573 )
 f = 2,734.10-6 Hz
 T = 1 / f = 365,7.103 s
5. On peut montrer que le rayon de rotation a une valeur proche de rPég. = 590.106 m.
En déduire la masse de l’étoile à l’aide de la troisième loi de Képler : 
E.L : M = 
 =   = 9,09.1026 kg « Unité / CS /Arrondi »
Bonus : Si on s’ennuie en toute fin de TP, on pourra chercher à justifier l’expression (3) d’après les
informations fournies.
Quand la moto se déplace, l’observateur perçoit une fréquence différente selon si la moto se
rapproche ou s’éloigne de lui :
- fréquence perçue par l’observateur au bord de la route pendant l’approche : 
 (1)
- fréquence perçue par le récepteur au bord de la route pendant l’éloignement : 
 (2)
=> Les fréquences f1 et f2 sont déterminées par des mesures à l’aide d’instruments. fS la fréquence du
son de la moto immobile est inconnue. La vitesse VS de la moto a pour expression : 
 (3)
Bonus : On effectue le rapport [f1 – f2 / f1 + f2] à l’aide des formules (1) et (2) pour simplifier fS et on retrouve la formule (3) :