Un algorithme d`approximation pour le probl`eme One
Un algorithme d’approximation pour le probl`eme
One-Warehouse Multi-Retailers
Jean-Philippe Gayon, Guillaume Massonnet, Christophe Rapine,
Gautier Stauffer
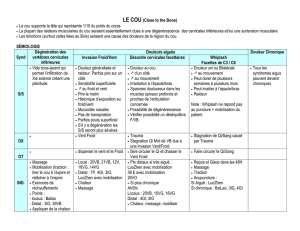
JFRO - mars 2013
1
2
R´eseau de distribution multi-´echelon
3
Le probl`eme OWMR
Retailerssupplier
0
1
N
Warehouse
External
•One Warehouse : un entrepˆot
•Multiple Retailers : Nd´etaillants, chaque d´etaillant idevant
satisfaire une demande dit `a la p´eriode t,
•Un horizon de temps discr´etis´e en Tp´eriodes.
•Chaque d´etaillant s’approvisionne aupr`es de l’entrepˆot,
•L’entrepˆot s’approvisionne aupr`es d’un fournisseur externe.
4
Coˆut d’une politique
i
K
0
h
i
h0
0Ki
•Coˆut fixe de commande Kipay´e si le site icommande
•Coˆut de possession hi
t(x)pay´e pour conserver une quantit´e x
en stock de la p´eriode t`a la p´eriode t+ 1 au site i
⇒minimiser le coˆut total du syst`eme sur l’horizon de temps
4
Coˆut d’une politique
i
K
0
h
i
h0
0Ki
•Coˆut fixe de commande Kipay´e si le site icommande
•Coˆut de possession hi
t(x)pay´e pour conserver une quantit´e x
en stock de la p´eriode t`a la p´eriode t+ 1 au site i
⇒minimiser le coˆut total du syst`eme sur l’horizon de temps
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
1
/
78
100%
