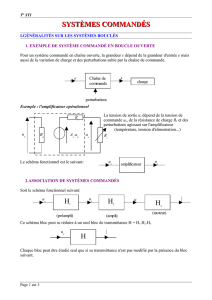
Système commandé en chaîne fermée

B.1.5 Notions de systèmes commandés en boucle fermé
1°) Systèmes commandés
1.1) Exemple
Un moteur à excitation séparée, il peut-être commandé par la tension u
appliquée à l’induit et la grandeur de sortie peut-être la vitesse angulaire.
1.2) Cas général
Tout dispositif, pour lequel le réglage d’une grandeur d’entrée E permet
l’obtention d’une grandeur de sortie S ne dépendant, en principe, que de E est un système
commandé.
On symbolise ce dispositif par un schéma unifilaire.
1.3) Fonction de transfert
Un système réel est modélisé par un système linéaire, qui est en général très
proche.
S = T . E avec T : fonction de transfert ou transmittance
2°) Système commandé en chaîne ouverte
2.1) Exemple
Le hacheur série permet d’alimenter le moteur M sous une tension réglable,
donc il permet d’ajuster sa vitesse de rotation.
Schéma unifilaire: hypothèse i = I = 0 A
Le rapport cyclique = k1 uc avec uc tension de commande.
Usmoy = et Usmoy =
Bernaud J 1/3
U0
us
i
LB
M
Charge
T
E S

B.1.5 Notions de systèmes commandés en boucle fermé
Détermination de la transmittance de la chaîne :
donc  est proportionnelle à uc.
En réalité, nous avons négligé la chute ohmique RI, nous avons donc
Pour une valeur de  déterminée, si la charge croît (le couple résistant
augmente), I augmente, donc K diminue car  U0 reste constant. Par conséquent le
moteur ralentit lorsque sa charge augmente, il faut provoquer une croissance de uc pour faire
croître.
2.2) Insuffisance de la chaîne ouverte
On voit que pour rendre cette correction automatique de la vitesse en
tenant compte de I, il faut corriger la tension de commande . Il faut ainsi adjoindre au système
précédent un ou des autres éléments permettant de contrôler .
3°) Système asservi en système bouclé
La chaîne précédente est appelée chaîne directe. L’élément permettant la
correction automatique est appelé chaîne de retour.
3.1) Chaîne de retour
Cette chaîne de retour peut-être fait par une dynamo-tachymètrique.
3.2) Opérateur de différence
Il peut-être constitué par un amplificateur de différence entre la tension
de retour et la tension d’entrée ( valeur de consigne) correspondant à la vitesse souhaitée.
Bernaud J 2/3

B.1.5 Notions de systèmes commandés en boucle fermé
3.3) Schéma fonctionnel de la boucle fermée
grandeur de
consigne
uc
Chaîne directe
Chaîne de retour
grandeur de
sortie
grandeur de
retour
ue
us
ur
H
K
3.4) Transmittance en boucle fermée
HK : fonction de transfert en boucle ouverte.
Si
1 1 HK
On a un système en contre-réaction ( réaction négative),
on fera de la régulation, le système sera stable.
Si
1 1 HK
On a une réaction positive, le système ne sera pas stable
on aura un oscillateur.
4°) Transmittance complexe
Si les grandeurs sont sinusoïdales et tous les éléments linéaires, on peut définir
des transmittances complexes et donc la transmittance complexe en boucle fermée.
Bernaud J 3/3
ue: tension
d’erreur
Exemple de
montage:
ur
uc
+
-