TD d`électrocinétique n 2 bis Méthode d`étude des réseaux linéaires

Lycée François Arago
Perpignan
M.P.S.I.
2012-2013
TD d’électrocinétique no2 bis
Méthode d’étude des réseaux linéaires
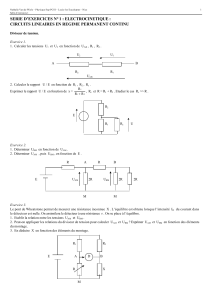
Exercice 1 - Analyse de la structure de réseaux.
Dans les quatre circuits, déterminer la résistance équivalente.
R1R2
R
Figure 1
R1RR2
Figure 2
RR2
R1
R3
Figure 3
RR2
R1
i=0
Figure 4
Exercice 2 - Utilisation des ponts diviseurs de tension.
1 . Déterminer la tension UBM en fonction de UAM .
2 . Déterminer les tensions UAM , puis UBM en fonction de E.
R
2R
UAM
R
2R
UBM 2RE
A B
M
Figure 5
Exercice 3 - Montage potentiométrique. Rendement en puissance.
On considère un potentiomètre dont le curseur C
mobile sépare le résistor Ren deux résistors xR et
(1 −x)R:
1 . Calculer en utilisant le théorème de Millman la
tension u′, puis en déduire l’intensité du courant i′.
2 . Retrouver l’expression de la tension u′par une
méthode plus directe en reconnaissant un montage
connu.
e e
i i
i′i′
r
u′r u′
xR
(1 −x)R
Figure 6
3 . Calculer la puissance reçue par r, notée P2, et la puissance fournie par le générateur, notée P1.
4 . Calculer le rendement en puissance du circuit : η=P2/P1.
A.N. :e= 24 V;R= 1,0kΩ ; r= 80 Ω ; x= 3/4.
1. et 2. Réponse : u′=xr
r+x(1 −x)Reet i′=x r+x(1 −x)Re
3. Réponse : P2=x2r
(r+x(1 −x)R)2e2
Penser à utiliser la formule du Pont Diviseur de Courantpour exprimer ien fonction de i′, on a
P1=r+xR
R(r+x(1 −x)R)e2
4. Réponse : η=x2rR
(r+xR) (r+x(1 −x)R)
S. Bénet 1

Exercice 4 - Pont de Wheatstone.
Le pont de Wheatstone permet de mesurer une résistance inconnue X. L’équi-
libre est obtenu lorsque l’intensité IDdu courant dans le détecteur est nulle.
On assimilera le détecteur à une résistance r. On se place à l’équilibre.
1 . Etablir la relation entre les tensions UAM et UBM .
2 . Peut-on appliquer les relations du pont diviseur de tension pour calculer
UAM et UBM ? Exprimer UAM et UBM en fonction des éléments du montage.
3 . En déduire Xen fonction des éléments du montage.
R1
R
R2X
E
D
A
B
Figure 7
1. Réponse : UAM =rID+UBM l’intensité IDétant orientée de Avers B.
2. Lorsque le pont est à l’équilibre, ID= 0. Réponse : UAM =R
R+R1
Eet UBM =X
X+R2
E
3. Réponse : X=RR2
R1
Exercice 5 - Étude d’un circuit linéaire.
On considère le circuit ci-dessous, comportant des résistors et des sources de tension ou de courant.
R
R
R
3R R
i
ue
e
η
1 . Déterminer les expressions de l’intensité du courant iet de la tension uen fonction des données de l’énoncé
1.1 . en utilisant uniquement les lois des mailles et les lois des nœuds, sans modifier le circuit ;
1.2 . en utilisant les lois d’association des dipôles linéaires et l’équivalence entre les représentations de Thévenin
et de Norton d’une source réelle afin de simplifier au maximum le montage ;
1.3 . en appliquant uniquement le théorème de Millman, sans modifier le circuit ;
2 . Calculer numériquement uet i, ainsi que la puissance reçue par le résistor parcouru par le courant d’intensité i.
Données : η= 50 mA ; e= 6,0 V ; R= 1,0 kΩ.
Réponse : i=η
2−e 6R
Exercice 6 - Générateur équivalent.
Donner les modèles de Thévenin et de Norton des
deux dipôles ci-contre.
2R
R
R
I
A B
Figure 8
R
R′
E
A B
Figure 9
S. Bénet 2/4

Exercice 7 - Circuit actif réductible à une résistance.
1 . Déterminer le modèle de Thévenin équivalent entre les bornes A et B.
2 . Donner la valeur de E pour laquelle le circuit est équivalent entre A et
B à une résistance pure dont on précisera la valeur.
A.N. :R= 5 Ω ; E1= 2 V;E2= 8 V.
E2
E1E
R
R
2R
R
2R
A
B
Figure 10
1. Le dipôle placé entre les bornes Aet Bpeut être représenté par son modèle de Thévenin caractérisé par :
Req =R, Eeq =E2−E1
4−E 2dirigé de Avers B
2. Le dipôle placé entre les bornes Aet Best équivalent à un résistor de résistance Rsi E=E2−E1
2
Exercice 8 - Association en parallèle.
Déterminer par les différentes méthodes de résolution l’inten-
sité du courant passant à travers la résistance R4.
E1
E2
R1
R2
R3R4
I0
Figure 11
Pour vous entraîner, retrouvez les résultats en utilisant toutes les méthodes du cours.
Réponse : I=R1R2R3
(R3+R4)R1R2+ (R1+R2)R3R4I0+E1 R1
+E2
R2dirigé vers le bas.
Exercice 9 - Calculs de résistances équivalentes.
Déterminer la résistance équivalente des réseaux suivants.
R R
R R
R RR
Figure 12
R R
R R R
R R
R R R
R R
Figure 13
R R
RRR
R R
RRR
R R
Figure 14
r
r
r
r
r r
Figure 15
S. Bénet 3/4

Exercice 10 - Équivalence triangle - étoile : théorème de Kennely.
1 . Déterminer r1,r2et r3en fonction de R1,R2et R3pour que les deux réseaux soient équivalents.
R3
R1R2
AB
C
Figure 16
r2
r3
r1
AB
C
Figure 17
2 . Applications
2.1 . Déterminer la résistance équivalente de l’as-
sociation de résistances identiques ci-contre.
R2R1
R1R2
R3
Figure 18
2.2 . Calculer l’intensité du courant qui circule dans la
résistance r.
A.N. :E1= 2,5V;E2= 3,0V;R= 10 Ω ; R= 2,0 Ω.
R R
E1rE2
R R
R
Figure 19
S. Bénet 4/4