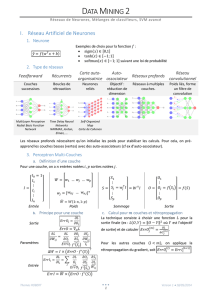
Vers un critère d`arrêt de Boosting basé sur la

Vers un critère d’arrêt de Boosting basé sur la diversité
des classifieurs
Nida Meddouri, Hèla Khoufi Zouari, Mondher Maddouri
Unité de Recherche en Programmation, Algorithmique et Heuristiques - URPAH
Faculté des Sciences mathématiques, physiques et naturelles de Tunis - FST
Université d’El Manar, Campus universitaire El Manar, 1060, TUNIS, TUNISIE
[email protected], hela.khoufi[email protected],
mondher[email protected]
RÉSUMÉ. Dans cette dernière décennie, plusieurs chercheurs se sont intéressés aux méthodes de
Boosting pour améliorer la performance des classifieurs. Néanmoins, l’ajout de classifieurs ne
garantit pas, toujours, cette amélioration mais induit plutôt un phénomène de sur-apprentissage.
Dans cet article, le rôle de la diversité sur la performance des ensembles de classifieurs est ex-
ploité au cours de l’apprentissage. Une mesure permettant d’évaluer cette diversité est utilisée.
L’étude expérimentale sur des bases différentes montre la relation entre la diversité des classi-
fieurs et la performance de Boosting.
ABSTRACT. In the last decade, many researchers were interested in Boosting methods to improve
the performance of classifiers. However, the addition of more classifiers does not always guar-
antee this improvement but rather induces a phenomenon of Over-fitting. In this paper, the role
of diversity on the performance of classifiers is exploited during learning process. To calculate
this diversity, QStatistic measure is used. The experimental study on different data sets shows
the relationship between classifier diversity and the performance of Boosting.
MOTS-CLÉS : Classification, Boosting, Ensemble de classifieurs, Diversité, Sur-apprentissage.
KEYWORDS: Classification, Boosting, Classifier ensembles, Diversity, Over-fitting.

1. Introduction
Avec le développement des outils informatiques, nous avons assisté ces dernières
années à un véritable déluge d’informations stockées dans de grandes bases des don-
nées scientifiques, économiques, financières, médicales, etc [LEF 01]. Le besoin d’in-
terpréter et d’analyser de grandes masses de données a suscité beaucoup d’intérêt.
Ainsi, la mise au point des nouvelles techniques d’analyse est devenue un réel défi
pour la communauté scientifique. Pour répondre à cette pénurie de connaissances sur
les données, de nouvelles méthodes d’extraction de connaissances ont vu le jour, re-
groupées sous le terme générique de la fouille de données ou Data Mining [BER 04].
La fouille de données est une thématique de recherche en pleine évolution visant à
exploiter les grandes quantités de données collectées chaque jour dans divers champs
d’applications de différents domaines, tels que les statistiques, les bases de données,
l’algorithmique, les mathématiques et l’intelligence artificielle [LEF 01]. On lui donne
d’autres appellations, comme par exemple extraction de connaissances dans les bases
de données ou encore exploration de données. L’extraction de connaissances dans les
bases de données (ou Knowledge Discovery in Databases -KDD), désigne le proces-
sus interactif et itératif non trivial d’extraction de connaissances implicites, précédem-
ment inconnues et potentiellement utiles à partir des données stockées dans les bases
de données.
L’idée sous-jacente de la fouille de données est donc d’extraire les connaissances
cachées à partir d’un ensemble de données. Le terme fouille de données regroupe
un certain nombre de tâches, telles que la prédiction,le regroupement et la classifi-
cation. Ces tâches peuvent être faites par plusieurs techniques, telles que les arbres
de décisions,les réseaux de neurones ou l’analyse de concepts formels [LEF 01].
Ces classifieurs sont souvent appelés weak learners puisqu’ils produisent des perfor-
mances faibles. Récemment, un grand nombre de travaux, en apprentissage supervisé,
ont porté sur les méthodes de dopage (Boosting) de classifieurs qui sont des approches
de fouille de données permettant d’améliorer les performances des classifieurs faibles
par la combinaison de leurs résultats. La simplicité de mise en oeuvre et les théorèmes
récemment édictés, relatifs aux bornes, aux marges, ou encore à la convergence du
Boosting sont deux raisons principales à cette large utilisation [FRE 97].
Boosting construit d’une manière séquentielle un ensemble de classifieurs de même
modèle. Chaque classifieur est généré en fonction des données d’apprentissage et de
la performance du classifieur précédent. Grâce à la construction ingénieuse de ces
données, le Boosting favorise la diversité des classifieurs [BRO 05]. Toutefois, il a été
constaté que l’ajout de classifieurs pourrait avoir des effets ’paralysant’ dans le sens où
cela ne conduit pas à une amélioration implicite de la performance de Boosting, mais
plutôt à sa dégradation [SHI 02] à cause du sur-apprentissage [KUN 02b] [BüH 07].
Cela s’explique notamment par l’échantillonnage répétitif des données d’apprentis-
sage à partir des distributions similaires. Nous nous demandons donc si nous pouvons
utiliser la diversité de classifieurs pour arrêter le Boosting au bon moment.

Dans la section suivante, nous présentons une méthode adaptative pour la géné-
ration de classifieurs [FRE 97] et nous discutons de leur diversité. Dans la section
3, nous proposons un nouveau critère d’arrêt de Boosting basé sur une mesure de
diversité des classifieurs. Une étude expérimentale est présentée dans la section 4 per-
mettant d’expliquer le rôle de la diversité des classifieurs dans AdaBoost.
2. Boosting et diversité des classifieurs
2.1. Boosting des classifieurs
L’idée générale d’AdaBoost est de construire un nombre Tfixe de classifieurs
séquentiellement [FRE 97]. Initialement, AdaBoost affecte des poids égaux aux ’N’
exemples d’apprentissage oide l’ensemble O={o1,o2, ..., oN}. Chaque oiest éti-
queté par la classe yitel que yi∈Y={1, ... ,k}et kest le nombre de classes.
L’initialisation de la distribution des poids D0se calcule comme suit :
D0(i) = 1
Npour i = 1, ..., N. [1]
Le vecteur des poids est initialisé en utilisant [2] :
w1
i,y =D0(i)
k−1pour i = 1, ..., Net y∈Y− {yi}.[2]
Pour chaque itération t,Wt
iest calculé de la façon suivante :
Wt
i=X
y6=yi
wt
i,y pour tout y 6=yi[3]
La distribution des poids est mise à jour en utilisant la formule [4] :
Dt(i) = Wt
i
PN
i=1 Wt
i
.[4]
Chaque classifieur ht, construit, attribue à chaque exemple oiune probabilité pt(oi,yi)
estimée pour chaque classe yi. Cette probabilité prend la valeur 1 si oiappartient
réellement à la classe yiet 0 s’il n’appartient pas à la classe yi. Trois cas se présentent :
– Si pt(oi,yi) = 1 et pt(oi,y) = 0, cela signifie que ∀y6=yi,hta prédit correctement
la classe de oi.
– Si pt(oi,yi)=0etpt(oi,y) = 1, cela signifie que ∀y6=yi,hta proposé une réponse
inverse pour oi.
– Si pt(oi,yi) = pt(oi,y), cela signifie que, la classe de oiest sélectionnée aléatoi-
rement entre yet yi.

A partir de cette interprétation, la pseudo-perte du classifieur htvia la distribution
des poids Wtest définie par [5] :
t= 0.5×
N
X
i=1
Dt(i)(1 −pt(oi, yi) + X
y6=yi
qt(i, y)×pt(oi, y)) [5]
avec :
qt(i, y) = wt
i,y
Wt
i
pour tout y 6=yi.[6]
L’erreur est donc :
βt=εt
1−εt
.[7]
Les vecteurs des poids des exemples sont aussi mis-à-jour selon βtpour tout i=1,..,N
et y∈Y− {yi}:
wt+1
i,y =wt
i,y ×β0.5×(1+pt(oi,yi)−pt(oi,y))
t[8]
Après la génération de Tclassifieurs, le résultat du Boosting est déterminé via :
hfin(oi) = arg max
y∈Y
T
X
t=1
log 1
βt
×pt(oi,yi).[9]
2.2. Sur-apprentissage et diversité des classifieurs
D’après l’article de [SEB 03], la mise à jour adaptative des données, visant à aug-
menter le poids de ceux mal appris par le classifieur précédent, permet d’améliorer
la performance de n’importe quel algorithme d’apprentissage, supposé faible. Néan-
moins, les capacités d’AdaBoost ont été remises en cause dès qu’il utilise des données
fortement bruitées. Pour éviter le sur-apprentissage, [SEB 03] propose une nouvelle
méthode dite iAdaBoost qui permet de modifier les poids des exemples d’apprentis-
sage dans AdaBoost en tenant compte des données bruitées. Dans [BüH 07], les au-
teurs ont étudié les fonctions d’erreurs dans Boosting pour justifier le phénomène du
sur-apprentissage et ont montré la lenteur du Boosting à atteindre ce phénomène.
Classiquement, l’arrêt du Boosting se fait a priori après Titérations prédéfinie.
D’autres critères d’arrêt ont été proposés tel que early stopping qui se base sur la
validation croisée [ZHA 05]. Néanmoins, aucun des critères cités ne tient compte de
la diversité des classifieurs au cours de l’apprentissage.
D’après l’article de [KUN 02a], les classifieurs devraient être différents les uns des
autres sinon la décision de l’ensemble ne sera pas meilleure que les décisions indivi-
duelles. Cette différence, appelée aussi diversité, a été étudiée dans plusieurs travaux
[BRO 10]. Dans [KUN 02a], il est constaté l’avantage de la diversité des classifieurs
linéaires sur la performance d’AdaBoost pour des problèmes à deux classes. En effet,
les résultats ont montré que la performance d’AdaBoost est à son maximum quand

les classifieurs sont très diverses. Cela explique qu’il y ait un lien entre la diversité
des classifieurs linéaires et l’erreur d’AdaBoost. De nombreuses mesures ont été éga-
lement proposées pour calculer la diversité entre les classifieurs. Mais, il est prouvé
qu’il n’y a pas une meilleure mesure de diversité bien qu’elles soient nombreuses.
Dans cet article, on propose d’utiliser le QStatistique pour calculer la diversité
entre les classifieurs nominaux [MED 10]. En effet de nombreuses études de diversité
[KUN 02a] [KUN 02b] recommandent vivement cette mesure puisqu’elle est simple
et a une valeur nulle pour les classifieurs indépendants ce qui facilite l’interpretation
de son utilisation. Cette mesure se calcule entre chaque paire de classifieurs hiet hj
en utilisant la formule [10] :
Qj,k =N11N00 −N10N01
N11N00 +N10N01 [10]
Sachant que Nvw (v={0,1} et w={0,1}) est le nombre des exemples oide l’en-
semble Oclassés correctement/incorrectement par les deux classifieurs hjet hk(pour
tout j= 1, ...,tet k= (j+1), ...,t) selon le tableau 1.
hkcorrect (1) hkincorrect (0)
hjcorrect (1) N11 N10
hjincorrect (0) N01 N00
N=N00+N01+N10+N11
Tableau 1. Le nombre d’accords et de désaccords entre deux classifieurs.
La diversité d’un ensemble de Tclassifieurs est calculée en faisant la moyenne des
diversités des différents paires.
Dans la section suivante, nous discutons un nouveau critère qui permet d’arrêter le
sur-apprentissage en se basant sur la diversité des classifieurs.
3. Contribution théorique
Dans les études de [KUN 02a] et [AKS 06], la mesure Qstatistique est utili-
sée principalement pour mesurer la diversité entre les classifieurs. La publication
[BRO 05] montre que les classifieurs indépendants peuvent offrir une amélioration re-
marquable des performances dans le Boosting. A partir des expérimentations menées
par [KUN 02a] et [KUN 02b] sur des échantillons différents de données, les auteurs
ont prouvé que la diversité négative des classifieurs mis en jeu est préférable. En plus,
avec un petit nombre de classifieurs, les ensembles générés sont très divers. Mais, plus
le nombre de classifieurs augmente, plus la diversité diminue.
Nous pensons que l’on peut arrêter le sur-apprentissage dans le Boosting en utili-
sant la mesure QStatistique puisque la variation de cette mesure devient stationnaire
lors du sur-apprentissage.