td :application du premier principe de la thermodynamique a la chimie

1
Thermodynamique Chapitre 1
TD : APPLICATION DU PREMIER PRINCIPE DE LA THERMODYNAMIQUE A LA
CHIMIE
Exercice 1: Enthalpie standard de formation du benzène
Enoncé :
1. Calculer l’enthalpie standard de formation du benzène liquide à 298K, connaissant à cette température :
-
combustionH°(C6H6(l))=-3265 kJ/mol - fH°(CO2(g))=-393 kJ/mol - fH°(H2O(l))=-286 kJ/mol
Correction :
6 C(graphite) + 3 H2(g) = C6H6(l)
|  ↑
| | 
| + 6 O2(g)  | - 7,5 O2(g)
↓ +1,5 O2(g) |
6 CO2(g) + 3 H2(g) --------------------> 6 CO2(g) + 3 H2O(l)
On a donc:    
Exercice 2 : Liaison C-H
Enoncé :
On donne à 298 K :
dissH°(H-H)=432 kJ/mol combH°(CH4(g))=-890,34 kJ/mol
fH°(H2O(l))=-285,84 kJ/mol subH°(C(graph))=705,15 kJ/mol fH°(CO2(g))=-393,51 kJ/mol
1. Calculer dissH°(C-H).
L’énergie de la liaison de la molécule diatomique AB (en eV), est l’équivalent microscopique de l’enthalpie standard de
dissociation de la liaison, notée
dissH°(T) (en J/mol), lorsqu’une mole de AB(g) donne deux radicaux A°(g) et B°(g) sans
interaction :
AB(g) = A°(g) + B°(g)
dissH°(T)=NA.e.El,AB=NA.e.DAB>0
Correction :
C(g) + 4 H(g) = CH4(g)
|  ↑
| | 
|  | - 2 O2(g)
↓ +1,5 O2(g) |
C(graphite) + 4 H(g) CO2(g) + 2 H2O(g)
| ↑
|  | 
|  | + O2(g)
↓ + O2(g) |
C(graphite) + 2 H2(g) --------------------> CO2(g) + 2 H2(g)

2
Exercice 3: Energie réticulaire
Enoncé :
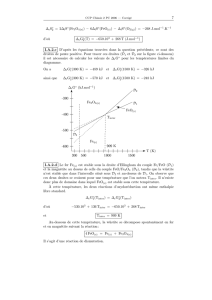
1. Calculer l’énergie réticulaire du cristal d’oxyde ferreux FeO compte tenu des données à 298K:
Formation de FeO :
fH°(FeO(s))=-267,94 kJ/mol
Energie de liaison de O2 :
dissH°(O2)=493 kJ/mol Sublimation du fer : subH°(Fe(s))=397,5 kJ/mol
Energie de 1ère ionisation du fer : EI1(Fe)=7,9 eV Energie de 2ème ionisation du fer : EI2(Fe)=16,18 eV
Energie nécessaire pour former O2-(g) à partir de O(g) : AE(O)=-8 eV
NA=6,02.1023 mol-1 e=1,6.10-19 C
On assimile l’énergie réticulaire Eret d’un cristal ionique à l’enthalpie standard de la réaction de dispersion au cours de
laquelle 1 mole de cristal est dissociée en ses ions constitutifs gazeux, sans interaction :
CxAy(s) = x Cp+(g) + y Aq-(g)
retH°=Eret.NA.e
Correction :
Valeurs macroscopiques des énergies microscopiques : -  
-   - 
Energie réticulaire macroscopique du cristal :
FeO(s) = Fe2+(g) + O2-(g)
|  ↑
| | 
| | - e-
↓ |
Fe(s) + ½ O2(g) Fe+(g) + O2-(g)
| ↑
|  | 
| 
 + 2 e- | - e-
↓  |
Fe(g) + O(g) --------------------> Fe(g) + O2-(g)
Energie réticulaire microscopique :  

3
Exercice 4 : Température de flamme
Enoncé :
1. Rechercher la température de flamme lors de la combustion du gaz de ville, constitué essentiellement de méthane dans
un excès d’air (assimilé au mélange O2/N2 avec n(N2)=4n(O2)). Pour l’application numérique, on considérera que
n(O2)=2.n(CH4)=2.n0
Données :
vapH°(298K,H2O(l))=43,84 kJ/mol combH°(298K,CH4(g))=-890,4 kJ/mol
Corps
O2(g)
CO2(g)
N2(g)
H2O(g)
H2O(l)
CPm° J.K-1.mol-1
30,0+4,2.10-3T
44,2+9,0.10-3T
27,9+4,3.10-3T
30+10,7.10-3T
75,5
Correction :
Il s’agit d’une température de flamme, on travaille sur des transformations isobares. Les enthalpies de combustion et de
vaporisation étant données à 298 K, on commence par réaliser la transformation chimique à Ti.
| Etat 1 Réaction | Etat 2 Echauffement | Etat 3
| Ti -----------> | Ti -------------------> | Tf
|  = 0 à Ti | f des produits | f
La transformation considérée étant adiabatique et isobare : 
Bilan de matière lors de la réaction (détermination de l’avancement final) :
mol
CH4(g) + 2 O2(g) = CO2(g) + 2 H2O(g)
N2
EI
n0
2.n0
0
0
8.n0
EF
0
0
n0
2.n0
8.n0
L’avancement final est donc : f = n0.
Variations d’enthalpie :  
Température de flamme :
Equation du second degré en Tf :  

4
Exercice 5 : Combustion du méthanol
Enoncé :
On réalise, dans un calorimètre adiabatique et sous pression constante, la combustion d’un échantillon de
méthanol liquide de masse m égale à 0,4867 g. En présence d’un excès de dioxygène, la réaction est totale et fournit
exclusivement du dioxyde de carbone gazeux et de l’eau liquide. La valeur initiale de la capacité calorifique à pression
constante du système (c'est-à-dire du mélange réactionnel avant réaction et du calorimètre) est notée CP=5,580.103 J.K-1.
Au cours de la réaction, la température de l’ensemble passe de 23,56°C à 25,54°C.
1. Etablir l’équation-bilan de la réaction et déterminer l’enthalpie standard de combustion correspondante.
Correction :
Equation de la réaction : CH3OH(l) + 3/2 O2(g) = CO2(g) + 2 H2O(l)
La pression étant constante lors de la réaction, il faut raisonner en enthalpie.
L’énoncé fournit la valeur de CP avant la réaction, il faut donc décomposer le processus réel de la façon suivante :
| Etat 1 Echauffement | Etat 2 Réaction | Etat 3
| Ti --------------------> | Tf ------------> | Tf
|  = 0 sans réaction |  = 0 à Tf | f
Variation d’enthalpie lors des deux étapes :  
Avancement final de la réaction :  
Le calorimètre est adiabatique et l’évolution isobare :  
Enthalpie standard de réaction à la température finale :