Université Paris Descartes — UFR Math-Info Année 2016

Universit´ e Paris Descartes —UFR Math-Info Ann´ ee 2016-2017
Licence 2e ann´ ee Environnement de Calcul Scientifique et Mod´ elisation
page web du cours : http://www.mi.parisdescartes.fr/˜moisan/ecs/
Exercices 34 `a 36
Exercice 34 (th´eor`eme des nombres premiers).
1) Ecrire une fonction t = test premier(n) qui prend en entr´ee un entier n>1 et renvoie
un vecteur tde bool´eens, de taille n, tel que t(k) est vrai si et seulement si kest premier (on
rappelle qu’un entier naturel k>2 est premier s’il n’est divisible que par 1 et lui-mˆeme).
On utilisera la m´ethode du crible d’Eratosth`ene pour construire t. V´erifier la fonction pour
n= 20, et estimer l’ordre de grandeur du n maximal atteignable en un temps raisonnable
(quelques secondes). On utilisera la commande stacksize une fois pour toutes afin de disposer
du maximum de m´emoire (RAM) possible.
2) Ecrire une fonction l = premiers(n) qui prend en entr´ee un entier n>1 et renvoie
dans le vecteur lla liste des nombres premiers compris entre 1 et n. V´erifier la fonction pour
n= 100.
3) Ecrire une fonction N = compte premiers(n) qui prend en entr´ee un entier n>1 et
renvoie un vecteur Nde taille ntel que N(k) soit ´egal au nombre de nombres premiers
compris entre 1 et k. V´erifier la fonction pour n= 20. Tester exp´erimentalement, en tra¸cant
(commande plot) le graphe de la fonction k7→ N(k) log(k)/k, le th´eor`eme des nombres
premiers, qui ´etablit que la limite de cette fonction vaut 1 quand ktend vers l’infini. La
convergence semble-t-elle rapide ?
Exercice 35 (conjecture de Goldbach).
La conjecture de Goldbach (datant de 1742, non d´emontr´ee `a ce jour, mais l’objet de
nouveaux r´esultats en 2013) pr´etend que tout entier pair sup´erieur ou ´egal `a 4 peut s’´ecrire
comme la somme de deux nombres premiers.
1) Ecrire une fonction N = goldbach ok(n) qui prend en entr´ee un entier n>1 et renvoie
un vecteur Nde bool´eens de taille ntel que N(k) est vrai ssi l’entier 2kpeut s’´ecrire comme
la somme de deux nombres premiers. On pourra utiliser le vecteur p = premiers(2*n) (voir
exercice 34), et la matrice Sde terme g´en´eral S(i,j) = p(i)+p(j) (autrement dit, N(k) est
vrai ssi l’un au moins des termes de Svaut k). A l’aide de la fonction goldbach ok, tester la
conjecture de Goldbach jusqu’`a l’entier le plus grand possible. Le facteur limitant est-il le
temps de calcul ou la quantit´e de m´emoire requise ?
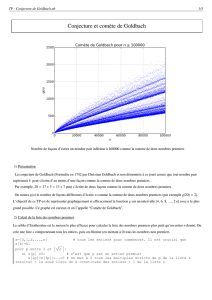
2) Plus g´en´eralement, ´ecrire une fonction N = comete goldbach(n) qui prend en entr´ee un
entier n>1 et renvoie un vecteur Nde taille ntel que N(k) soit ´egal au nombre de fa¸cons
d’´ecrire l’entier 2kcomme somme de 2 nombres premiers. Tracer par la commande
clf;plot(N,’.’,’markersize’,1)
le graphe de la fonction k7→ N(k), appel´e “com`ete de Goldbach”.
1

Exercice 36* (conjecture de P´olya).
´
Ecrire une fonction N = nombre facteurs(n) qui prend en entr´ee un entier n>1 et renvoie
un vecteur Nde taille ntel que N(k) soit ´egal au nombre de facteurs premiers de k. Ecrire
ensuite une fonction L = Liouville(n) qui prend en entr´ee un entier n>1 et renvoie un
vecteur Lde taille ntel que L(k) soit ´egal `a la somme pour i= 1 `a kdes (−1)N(i)avec les
notations pr´ec´edentes. Tracer le graphe de L(appel´ee fonction de Liouville) calcul´ee pour
n= 1000,10000,100000, et tester aussi loin que possible la conjecture de P´olya, qui pr´etend
que L(k)60 pour tout entier k>1.
2