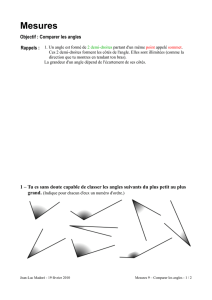
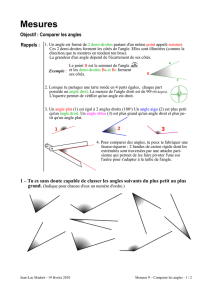
Angles - La tache

Sommaire
1 Rappels et définitions. 2
2 Angles adjacents. 4
3 Angles supplémentaires et complémentaires. 6
4 Angles opposés par le sommet. 8
4.1 Définition................................ 8
4.2 Propriété des angles opposés par le sommet. . . . . . . . . . . . . 9
5 Angles alternes-internes. 10
5.1 Définition................................ 10
5.2 Propriétés des angles alternes-internes. . . . . . . . . . . . . . . . 11
6 Angles correspondants. 12
6.1 Définition ............................... 12
6.2 Propriétés des angles correspondants. . . . . . . . . . . . . . . . . 13
1

Chapitre 1
Rappels et définitions.
sommet deux côtés
Figure 1.1 – Angle
Dans cet exemple, le sommet de cet angle est Aet ses côtés sont les segments
[AB]et [AC]
Remarques
– Cet angle est marqué (c’est le petit arc de cercle vert)
– Les deux côtés de cet angle sont des segments.
– La mesure de cet angle est plus grande que 90°, c’est un angle obtus.
– Cet angle s’appelle
\
BAC ou
\
CAB (le sommet est toujours au milieu de
la notation).
2

Cours sur les angles - classe de cinquième
Voici un autre exemple d’angle.
Figure 1.2 – Angle
Le sommet de cet angle est Aet ses côtés sont les demi-droites [Aa)et [Ab)
Remarques
– Cet angle est marqué (c’est le double petit arc de cercle orange)
– Les deux côtés de cet angle sont des demi-droites (aet bne sont pas des
points mais le nom des 2 demi-droites).
– La mesure de cet angle est plus petite que 90°, c’est un angle aigu.
– Cet angle s’appelle
d
bAa ou
d
aAb (le sommet est toujours au milieu de la
notation).
3

Chapitre 2
Angles adjacents.
Deux angles sont adjacents si ils ont un sommet en commun et si ils sont
de part et d’autre d’un côté en commun.
Figure 2.1 – Angles adjacents
Dans cette figure, les angles
\
BAC ou
\
CAD sont adjacents,
car ils ont le sommet A en commun et ils sont de part et d’autre du côté [AC].
4

Cours sur les angles - classe de cinquième
Certaines figures sont trompeuses.
Figure 2.2 – Angles non adjacents
Dans cette figure, les angles
\
BAD ou
\
CAD ne sont pas adjacents,
car ils ne sont pas de part et d’autre du côté commun [AD]
Figure 2.3 – Angles non adjacents
Dans cette figure, les angles
\
BAC ou
\
EAD ne sont pas adjacents,
car il n’ont en commun que le sommet A.
5