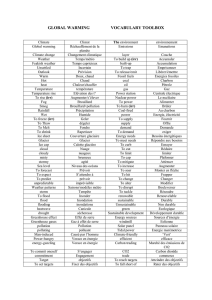
Représentations de Weil pour les groupes de similitudes et

UNIVERSITÉ PARIS-SUD 11
FACULTÉ DES SCIENCES D’ORSAY
THÈSE
Présentée pour obtenir
LE GRADE DE DOCTEUR EN SCIENCES DE
L’UNIVERSITÉ PARIS-SUD XI
Ecole doctorale: Mathématiques de la région Paris-Sud
Spécialité: Mathématiques
par
Chun-Hui WANG
Représentations de Weil pour les groupes de similitudes
et changement de base
Soutenue le 03, Juillet, 2012 devant la Commission d’examen:
M. Guy Henniart (Directeur de thèse)
Mme. Colette Moeglin (Rapporteuse)
M. Brooks Roberts (Rapporteur non présent)
Mme Laure Blasco (Examinatrice)
Mme Corinne Blondel (Examinatrice)
M. Laurent Clozel (Examinateur)
M. Paul G´ erardin (Examinateur)

Thèse préparée au
Département de Mathématiques d’Orsay
Laboratoire de Mathématiques (UMR 8628), Bât. 425
Université Paris-Sud 11
91 405 Orsay CEDEX

Résumé
La présente thèse s’inscrit dans le cadre de travaux sur la représentation de Weil. Elle con-
siste en trois parties. Aux chapitres 2 et 3, on généralise la correspondance de Howe aux groupes
de similitudes sur un corps local non archimédien de caractéristique résiduelle impaire. Aux
chapitres 4 et 5, on répond dans beaucoup de cas à une question, soulevée par V. Drinfeld, sur
la représentation de Weil de GS p8(F) de restreinte à un groupe GL2(A), où Aest une algègre
étale sur un corps local ou fini F. D’autre part, au chapitre 5, on montre que sur un corps fini,
les représentations de Weil sont compatibles au changement de base au sens de Shintani-lift.
Mots-clefs : groupe de similitudes, représentation de Weil, correspondance de Howe, change-
ment de base.
The representation of Weil for the similitudes groups and base change
Abstract
This present thesis is working on the Weil representation. It consists of three parts. In
chapter 2 and chapter 3, we generalize the Howe correspondance for the similitudes groupes
over the non archimedien field with odd residual characteristic. In chapter 4 and chapter 5, we
answer one question, raised by V. Drinfeld, about the restriction of the Weil representation of
the group GS p8(F) to GL2(A) where Ais an étale algebra over a non archimedien field or a
finite field F. On the other hand, in the chapter 5, we prove that in finite field case, the Weil
representations are invariant under the operator of base change in the sens of Shintani-lifting.
Keywords : similitude group, Weil representation, Howe correspondence, base change .

Remerciements
Je voudrais avant tout remercier mon directeur de thèse Guy Henniart, qui m’a proposé ce sujet et qui a dirigé
cette thèse. Je le remercie vivement pour ses aides pendant ces quatre dernières années, ainsi que ses idées, et ses
nombreuse remarques sur cette thèse.
Je tiens à remercier Colette Moeglin pour avoir accetpé de rapporter ce travail, et pour ses cours et son beau
livre sur ce sujet.
Je tiens à remercier Brooks Roberts pour avoir accetpé d’écrire un rapport sur cette thèse et ses articles sur ce
sujet.
Je remercie également Laure Blasco, Corinne Blondel, Laurent Clozel, Paul Gérardin de faire partie de mon
jury de thèse.
Je voudrais exprimer ma gratitude envers le Programme ALGANT et l’université Paris Sud qui m’ont fourni
les finances quand je fais mathématiques en Master et en Thèse.
Je remercie les membres du département mathématique à Orsay, plus particulièrement à Gérard Laumon pour
son encouragement, à Jean-Marc Fontaine et David Harari pour leurs cours, à la secrétaire Valérie Lavigne et aux
membres de bibliothèque pour leurs aides.
Je tiens ensuite à remercier les professeurs chinois : Xiaonan Ma(Paris 6, France), Yangbo Ye(Iowa, les États-
Unis), Tian Ye(CAS, Chine), Linsheng Yin(Tsinghua, Chine), pour leurs encouragements et aides.
Je voudrais remercier aussi les doctorants ou ex-doctorants : Ramla Abdellatif, Brembilla Caroline, Yinshan
Chang, Ke Chen, Li Chen, Miaofen Chen, Zongbin Chen, Marco De Ieso, Yiwen Ding, Ziyang Gao, Hatem Hajri,
Yong Hu, Yongquan Hu, Xun Jiang, Zhi Jiang, Arno Knet, Tingyu Lee, Wen-Wei Li, Xiangyu Liang, Chengyun
Lu, Shu Shen, Xu Shen, Shenghao Sun, Zhe Sun, Shun Tang, Jinglong Tong, Haoran Wang, Shanwen Wang, Hao
Wu, Guodong Zhu.

Table des matières
1 Préliminaires généraux 14
1.1 Les sous-groupes de Howe réductifs de S p(W) ........................... 14
1.2 Le groupe métaplectique M p(W)................................... 15
1.3 Les paires duales de Howe pour M p(W)............................... 18
1.4 Le groupe métaplectique de similitude GM p[B](W) ......................... 24
1.4.1 La constitution de Barthel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
1.4.2 Lecasgénéral ........................................ 26
1.5 LesreprésentationsdeWeil...................................... 27
2 La propriété du graphe 29
2.1 Le plus grand quotient du groupe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.2 Les quotients pour le produit de deux groupes . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.3 Les représentations de graphe forte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
2.4 Les représentations de bigraphe forte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
2.5 Appendices .............................................. 41
2.5.1 Le Théorème de Clifford(I)Casabélien........................... 41
2.5.2 Le Théorème de Clifford(II)Cascyclique.......................... 44
3 Représentations de bigraphe forte de groupes similitudes 45
3.1 Un sous-groupe intermédiaire Γde M p(W) ............................. 45
3.2 DesLemmes ............................................. 51
3.3 Constitution des représentations de bigraphe forte . . . . . . . . . . . . . . . . . . . . . . . . . . 53
3.3.1 Lecasdesgroupesscindés.................................. 53
3.3.2 ExemplesI .......................................... 56
Cas(1) ............................................ 56
Cas(2) ............................................ 57
Cas(3) ............................................ 57
Cas(1)’............................................ 57
Cas(2)’............................................ 57
3.3.3 Le cas des groupes non scindés . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
3.3.4 ExemplesII.......................................... 60
Cas(1) ............................................ 61
Cas(2) ............................................ 61
Cas(3) ............................................ 61
Cas(1)’............................................ 61
Cas(2)’............................................ 62
3.4 Appendice............................................... 62
3.4.1 Définition de H2(G,A).................................... 62