IV Les Nombres premiers Jumeaux

IV,1
Titre IV
Les Nombres Premiers Jumeaux

IV,2
IV.1 Introduction
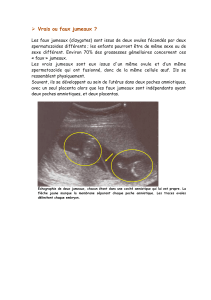
Ces fameux nombres jumeaux valent un titre à part. Tant d’illustres mathématiciens s’y sont intéressés ! Et même,
toute paléo interprétation mise à part, on en trouve deux paires sur l’os d’Ishango.
IV.2 Rappel
IV.2.1 Ecriture des nombres jumeaux
Tout nombre premier étant évidemment premier par rapport à 2 et à 3 peut aussi s’écrire sous la forme
6q
η +
;
1 η = ±
est en effet le seul reste possible de la division par 6 d’un nombre qui n’est divisible ni par 2 ni par 3. Les
nombres premiers en 2 et 3 se regroupent donc par paires dont la différence vaut 2. On dit qu’ils sont jumeaux ;
chaque couple de jumeaux comporte un cadet (
61
q−
) et un aîné (
61q+
) ayant le même paramètre q.
Ces couples sont strictement premiers si et seulement si cadet et aîné sont tous deux strictement premiers
IV.2.2 Les jumeaux sont premiers entre eux, qu’ils soient strictement premiers ou non.
Cf. titre II.2.3
IV.2.3 Critère de primalité
Cf. titres II.6.1à 4
Un nombre aîné
6 17q+≥
est premier si et seulement si
( )
premiermod(6 ) 6 61qi i i q
ηηη
≤
≠ + ∀+ 
+
Un nombre cadet
6 15q−≥
est premier si et seulement si
()
premier
mod(6 ) 6 61qi i i q ηηη ≤
≠− + ∀ + 
−
Ainsi, des jumeaux
61q±
seront tous deux premiers si et seulement si
()
premiermod(6 ) 6 61
qi i i q ηηη ≤
≠± + ∀ +  +
IV.3 Quantité illimitée des jumeaux premiers.
Les jumeaux composés ou non sont premiers entre eux ; on dit encore qu’ils sont indépendants, ou encore étrangers
l’un par rapport à l’autre. D’autre part, cadets et aînés de même paramètre ont une répartition voisine si bien qu’ils se
côtoient sans cesse. Sans constituer une preuve formelle, ces propriétés constituent la raison profonde de la quantité
illimitée des jumeaux premiers : indépendance et voisinage les laissent libres de former, ou non, des couples de
jumeaux premiers, indéfiniment.
Nous allons en donner une preuve rigoureuse.

IV,3
IV.3.1 Application du critère de primalité aux jumeaux premiers
Nous invitons le lecteur à consulter le titre précédent que nous résumons ci-dessous.
Deux nombres jumeaux
61
q±
, déjà premiers en 2 et 3, seront aussi premiers par rapport à
35,..., k
pp=
si et
seulement si leur paramètre commun q vérifie les conditions ci-dessous :
( ) ( )
,,
mod 6 | 6
ii k
qr i r i i p
ηη
ηη ≡ + ≠± ∀ + ≤
Cette double condition exprime que le reste de la division du paramètre q par tout nombre premier
6i η +
inférieur
ou égal à
k
p
doit être différent en valeur absolue du paramètre i de ce nombre premier. Pour des raisons de
symétrie nous choisissons des restes
i
r
η
par excès ou par défaut ; ils peuvent donc être positifs ou négatifs et leur
valeur absolue restera inférieure à la moitié (moins
1
2
) du diviseur premier (donc impair)
6i
η
+
.
Nous utilisons pour
i
r
η
ou
j
r
, le même type de notation que pour
i
p
η
; ainsi
ij
rr
η
=
est le reste de la division de q
par
6
j
ip η
+=
.
Il y a chaque fois
62i η +−
restes admissibles dont les valeurs successives sont
( ) ( )
3 ,..., 1 ,iii
η − + −+ −
( )
, 1 ,...,0,..., 1, iii −− −+
( )
, 1,..., 3ii η ++
Par exemple :
615 1| 1 2,
i
i ir
η
−= = ⇒ − −=,0, 1+ou 2
6 1 7 | 1 3, 2, 1
i
i ir
η
+
+= = ⇒ =−− −10,
,+2 ou 3
6 1 11 | 2 25,4,3,
,
i
i ir
η
++
−= = ⇒ = −− −−1, 0, 1, 2
,−++3, 4 ou+5,++
L’existence de deux jumeaux
61q±
premiers par rapport à
3
5,...,
k
pp=
relève donc du théorème des restes
chinois, car
( )
( )
()
33
44
mod 5
mod 7
......................
mod 6
jk
qr p
qr p
qr p j
η
η
≡=
≡=
≡=+
(4.1)
les deux valeurs
i±
étant, chaque fois, interdites au reste
i
r
η
de la division du paramètre q par les nombres premiers
successifs
6i η +
.
Posant
3
k
jk
j
p
=
= Π
∏
, les congruences (4.1) ont une solution commune
mod
nk nk k k
q re≡⋅ Π
et le nombre de
solutions
6
nk
q
η +
premières jusqu’en
k
p
est égal à
()( )( ) ( )
5 2 7 2 11 2 .......... 2
kk
Np=−− − −
(4.2)
dans chaque intervalle fermé inférieurement d’extension
k
Π
.
Lorsque
k
p
augmente indéfiniment,
k
N
augmente encore plus vite.

IV,4
A chaque vecteur
nk
r
et donc à chaque paramètre
nk
q
correspond
• soit un couple de jumeaux strictement premiers,
• soit un couple de jumeaux tous les deux premiers par rapport à
5,..., k p
seulement, mais dont l’un au
moins est multiple de facteurs supérieurs à
k
p
(ce que nous abrégeons en disant que ces jumeaux sont
premiers jusqu’en
k
p
seulement).
Ces couples ont pour expression
( )
6 1 mod
nk k
q±Π
.
Ainsi dans l’intervalle
( )
0,
k
Π
, on trouve
k
N
paramètres de couples de jumeaux qui sont, soit premiers, soit
multiples de facteurs supérieurs à
k
p
.
Dans tous les autres intervalles
()
()
()
,1 0
kk
xx xΠ +Π ∀ >
on trouve la même quantité constante
k
N
de
paramètres de couples de jumeaux premiers jusqu’en
k
p
, certains de ces jumeaux pouvant être strictement
premiers. Cela n’a rien d’étonnant puisque l’on ajoute des multiples de
k
Π
à des nombres qui ne sont pas
divisibles par 2,3, 5,…et
k
p
. Les nombres jumeaux premiers jusqu’en
k
p
ont aussi leur horloge !
IV.3.2 Infinitude des couples de jumeaux strictement premiers
Démonstration :
D’après l’expression (4.2) appliquée à chaque intervalle d’extension
k
Π
( )()( ) ( )
5 2 7 2 11 2 .......... 2
kk
Np=−− − −
,
les nombres premiers
k
p
et les quantités
k
N
de jumeaux premiers jusqu’en
k
p
sont en bijection par l’intermédiaire
de leur ordinal k avec les nombres entiers k.
L’ensemble des quantités
k
N
est donc équipotent avec celui des nombres entiers. La limite de
k
N
est ainsi égale
à
0
ℵ
de même que celle de k et de
k
p
.
Plus prosaïquement, lorsque l’entier k devient infini, le nombre premier
k
p
d’ordinal k devient infini ; les nombres
premiers jusqu’en
k
p
deviennent strictement premiers et leur quantité
k
N
devient infinie.
Les couples de jumeaux premiers sont en quantité infinie
0
ℵ
IV.4 Densité limite des nombres premiers jumeaux
Le plus grand nombre aîné lié à l’intervalle
1
6
k
ik
p= Π
∏
a pour valeur
61
k
Π+
et dans chacun des intervalles
successifs de grandeur
6k Π
la densité des couples de jumeaux
61
nk
q±
premiers par rapport à
2,3,5,..., k p
s’écrit
() ( )( ) ( )
2
2
6 1 1 6 1 2 5 1 2 7 ..... 1 2 1 2 1
k
kk k k ii
dN p p
=
= Π+ = − − − = −
∏
(4.3)
Cette densité varie de
1/6
pour
( )
d'indice 32
k
pk= =
à 1,162 % pour,
( )
d'indice 379 75
k
pk= =

IV,5
Les nombres premiers les plus bas
( )
3,5,7,11,13
font plonger rapidement cette densité ; elle décroît ensuite
lentement de façon asymptotique vers zéro comme on peut le constater sur le graphique ci-dessous
Comparons, en effet, cette densité à celle de l’ensemble des nombres premiers laquelle s’écrit :
( )
2
111
2
k
i
i
p
=
−
∏
(4.4)
Effectuant le rapport des deux densités, on trouve
( )
22
12 11 1
11
kk
ii
ii
i
pp
p
= =
−= −−
−
∏∏
Ce rapport tend vers zéro car chacun de ses facteurs est inférieur à son correspondant dans (4.4) et comme la
densité des nombres premiers tend vers 0, la densité limite des jumeaux premiers jusqu’en
k
p
tend aussi vers 0,
mais infiniment plus « vite ». Or lorsque
k
p
tend vers l’infini, les jumeaux premiers jusqu’en
k
p
deviennent tous
premiers.
Il s’ensuit que pour les grandes valeurs de
k
p
il existe encore des couples de jumeaux premiers même si le rapport
de leur densité à celle des nombres premiers devient petit ; ceci provient de leur raréfaction qui est « affine » de
celle des nombres premiers.
Théorème :
La densité limite des jumeaux premiers est infiniment plus petite que celle des nombres premiers.