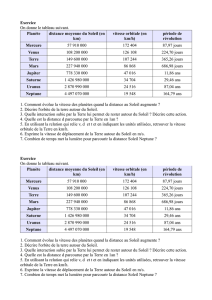
Mise en page 1

Quand la musique est bonne. Les planètes résonnent!
Un cas spectaculaire de résonances stables
Les planètes, entre elles et avec les autres corps, échangent de l’énergie. Et cela engendre plutôt des instabilités, catastrophique
dans le cas de la résonance 2:1 entre Jupiter et Saturne. N’y a-t-il pas de stabilité possible pour les corps du système solaire ?
Si : si l’on raisonne avec plus de 2 corps et que les effets des résonances peuvent se compenser avec les frottements.
Le cas le plus spectaculaire est celui de 3 satellites de Jupiter : Io, Europe et Ganymède. Ils sont tous les trois en résonnances
1:2:4. On peut croire que cela va être encore pire : si les trois s’alignent, les effets sur la plus lointaine, Ganymède, doivent être
démultipliés ? Et bien non ! Cela s’explique en tenant compte de toutes les résonances et des effets de marée.
Le scénario : les chercheurs pensent qu’il s’est déroulé ainsi : Io, en effet de marée avec Jupiter, tend à s’éloigner de celle-ci. Jusqu’à
ce qu’elle rencontre la résonance 2:1 avec Europe. Elle communique alors une partie de son énergie à Europe, jusqu’à ce qu’Europe,
à son tour, entre en résonance 2:1 avec Ganymède et lui transfère de l’énergie. L’énergie gagnée par chacun des satellites
ne sert donc pas à l’éloigner de sa position, elle est transférée sur le corps suivant.
Pour qu’un tel système reste en résonance stable, il faut tenir compte de plusieurs évènements qui dissipent ou diluent l’énergie
en trop :
• Io, soumise aux effets de marée conjoints de Jupiter et d’Europe, perd de l’énergie par “frottement”. Son intérieur est littéralement
malaxé par les effets de marée. Elle est ainsi le siège d’un volcanisme intense. Dans une proportion moindre, Europe et Ganymède
subissent des effets de marée, et leur intérieur est également chauffé, ce qui explique les failles dans leur surface de glace et
la possibilité qu’elles renferment un océan liquide souterrain.
• les trois satellites sont en décalage de phase et ne se retrouvent jamais
tous les trois en conjonction. Chaque fois que 2 se rencontrent,
le troisième est à l’opposé. Le transfert d’énergie ne se fait donc
pas d’un seul coup d’Io à Ganymède, mais de proche en proche.
• la rencontre Io-Europe se fait au périhélie d’Io et à l’aphélie d’Europe.
Et la rencontre Europe Ganymède se fait au périhélie d’Europe.
Ainsi Io a tendance à gagner en excentricité (ce qui est compensé par
la perte par effet de marée qui stabilise cette excentricité).
Europe, elle, a tendance à gagner de l’excentricité devant Io et à en
perdre devant Ganymède.
• Ganymède est de loin le plus gros des satellites, son inertie fait donc
que l’énergie qu’elle reçoit est difficilement convertie en mouvement.
• le processus est en cours : il va se poursuivre avec la captation de
Callisto en résonance 1:8 avec Io.
D’autres exemples
On peut noter plusieurs résonances de ce type dans les systèmes satellitaires, où les résonances orbitales se maintiennent grâce
à l’effet atténuateur d’autres résonances (notamment les effets de marée). Citons :
• les satellites de Saturne : 2:1 pour les couples Mimas-Téthys et Encelade-Dioné, et 4:3 pour Titan-Hypérion
• le système de Pluton-Charon, avec leurs satellites en résonance 1:1:3:5:6.
Quand les petits se planquent des gros
On a vu dans les cas de Jupiter et de la ceinture d’astéroïdes,
que les petits corps étaient éjectés des harmoniques de révolution
des grosses planètes. Dans la plupart des cas, il est vrai, les planètes
“font le ménage” dans les ceintures, mais il reste quelques corps qui
se calent dans des niches de résonances protégées :
• les Plutinos sont des objets de la ceinture de Kuiper ayant des
caractéristiques orbitales proches de Pluton : demi-grand axe,
excentricité, inclinaison. Ils sont tous en résonance 2:3 avec Neptune.
Pourquoi ne sont-ils pas éjectés ? Une forte inclinaison de leur orbite,
et un périhélie loin de celui de Neptune font qu’ils ne se rapprochent
jamais beaucoup de la planète : 17 UA au plus près. Neptune n’est
pas assez proche pour avoir un effet efficace. De plus, ces corps
s’approchent d’Uranus à 11 UA ce qui ajoute un effet contrant celui
possible de Neptune.
• les Troyens contre les Grecs. La résonance la plus stable est
la résonance 1:1 au point de Lagrange : le corps est sur la même orbite
que la planète mais décalé de 60° en avant ou en arrière. Ce sont des
zones de stabilité gravitationnelle forte, et toute une population de petits
corps s’y confine, protégés de toute autre influence.
Les planètes géantes ont chacune leurs cortèges de Grecs et de Troyens.
• les quasi-satellites : ce sont tous les corps qui font un tour du Soleil pendant que leur planète en fait 1 également : ce sont
des satellites en résonance 1:1. Les planètes en capturent en général un ou plusieurs pendant un certain temps (en milliers d’années,
ce qui est très court à l’échelle astronomique), puis les libèrent. Cruithne est en ce moment en résonance 1:1 avec la Terre.
Les planètes aussi sont en résonance
Les planètes géantes : c’est Jupiter qui donne le La, avec Saturne en 2:5, Uranus en 1:7 et Neptune en 1:14 (Uranus et Neptune
sont quasiment en 1:2).
Les planètes telluriques : Vénus et la Terre sont de masses équivalentes et mènent la danse. Elles sont ensemble en résonance
8:13, et le couple Terre Mars en 15:8.
Un avenir stable ?
Le système solaire a connu de profonds bouleversements dans le passé. Se dirige-t-il maintenant vers une douce seconde moitié
de vie, sans changement notable ? Pour les planètes géantes, probablement, mais pour les telluriques, c’est moins clair…
Jacques Laskar a réalisé une simulation prenant en compte toutes les influences mutuelles de planètes, paramètres et perturbations,
y compris la Relativité. Résultat : dans 1 % des cas, un événement catastrophique peut intervenir avant la fin de vie du Soleil :
échange d’orbite, éjection voire collision entre deux planètes. En fait, c’est l’excentricité de Mercure, assez importante, qui pourrait
amener des perturbations qui se propageraient à toutes les planètes internes.
1
c.c. Chetvorno
Faisons le calcul pour Jupiter et une sonde de 2 tonnes
Pour une même énergie cinétique échangée, on voit bien que la vitesse acquise par la petite sonde,
n’a rien de commun avec à la vitesse perdue par la grosse planète. Imaginons une sonde
de 2000 kg, profitant de la vitesse de Jupiter, et échangeant avec elle une énergie correspondant
à une augmentation de vitesse de v. L’énergie cinétique gagnée par le vaisseau est égale à l’énergie
cinétique perdue par Jupiter : ½ m v² =½MV² donc la vitesse perdue est .
M=2.1027 kg donc V =vx10-12
Jupiter perd mille milliards de fois moins de vitesse que le vaisseau n’en gagne. Si la sonde gagne
5 km/s, Jupiter perdra dans le même temps 5 µm/s. À l’inverse, si la sonde passe devant l’astre,
elle sera ralentie.
Pour comprendre en détail et tester le phénomène avec un jeu
À quel moment l’impulsion donnée au vaisseau est-elle la plus efficace ? Testez-le avec l’animation
sur cette page web :
http://www.sciences.univ-nantes.fr/sites/genevieve_tulloue/Meca/Planetes/transfert.html
Et pourquoi ne pas faire balancer l’électricité ?
Une résonance peut être mécanique, liée à la vibration propre des composants (comme dans
la musique), elle peut être liée à un champ gravitationnel (la balançoire), mais elle peut aussi
être électrique. Un circuit bien connu est celui mettant en série et en circuit fermé un condensateur
et une bobine.
Un condensateur électrique s’apparente à deux plaques parallèles qui peuvent accumuler
les charges électriques +d’un côté et - de l’autre. Une fois les plaques chargées, il peut se
comporter comme un générateur et fournir un courant. Inversement, le condensateur
peut recevoir un courant pour que ses plaques se chargent.
Une bobine est un fil enroulé sur lui-même dans lequel circule un courant. Mais quand un courant
circule, la bobine crée automatiquement un courant inverse.
Dans notre circuit, le condensateur, initialement chargé, se décharge dans la bobine, qui, au fur et
à mesure que le courant augmente, produit un courant inverse qui va recharger le condensateur.
On peut alors faire l’analogie avec la balançoire : le potentiel gravitationnel est alors
remplacé par la tension U aux bornes des composants (la tension électrique est d’ailleurs
appelée “différence de potentiel électrique”) et la vitesse par le courant qui circule.
Le condensateur joue le rôle d’accumulateur d’énergie potentielle. La bobine celui de la
“force de rappel” analogue à la force de gravitation de la Terre pour la balançoire.
Dans un tel circuit électrique, l’intensité du courant oscille avec une fréquence propre qui dépend
des caractéristiques de la bobine et du condensateur. Ces circuits sont utilisés notamment pour
filtrer les fréquences et ne laisser passer que celles qui sont proches de la fréquence de résonance
du système.
Comme aucun composant n’est parfait, il faut tenir compte des résistances électriques de chacun
d’eux, qui ont pour effet d’amortir le signal, et de faire perdre de l’énergie au circuit (sous forme
de chaleur), comme les frottements pour notre balançoire.
© NASA
23
456
789
10 11 12
1
/
1
100%

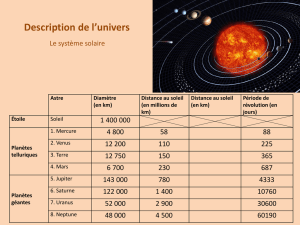




![syst solaire 4.ppt [Lecture seule]](http://s1.studylibfr.com/store/data/004573526_1-4d465d29ebcff0b08ba4dee35c865982-300x300.png)