IN201 : 5 – Algorithme de Dijkstra

IN201 : 5 – Algorithme de Dijkstra
Author : Christophe Garion <[email protected]>
Public : SUPAERO 2A
Date :
Résumé
Ce TP sert de récapitulatif aux quatre premières séances du cours IN201. Il consiste à concevoir et implanter un
système permettant de trouver un plus court chemin dans un graphe en utilisant l’algorithme de Dijkstra.
1 Objectifs
Les objectifs de ce TP sont les suivants :
– vérifier que vous êtes capable de proposer une solution de conception simple en utilisant le langage UML ;
– vérifier que vous êtes capable d’implanter une classe en respectant les principes énoncés en cours ;
– vérifier que vous êtes capable de tester une classe via JUnit.
2 Présentation du problème
Si une des grandes questions existentielles qui vous taraudent est de savoir comment touver un chemin minimal de votre
chambre au Batens histoire de profiter au maximum de votre lit douillet tout en évitant d’arriver en retard, ça tombe bien,
ce TP est pour vous.
Les problèmes de recherche de plus court chemin sont des problèmes bien connus en mathématiques et en informatique
depuis très longtemps. La représentation du chemin à parcourir se fait classiquement en utilisant un graphe composé de
nœuds représentant des points géographiques. Les nœuds peuvent être reliés entre eux deux par deux par des arcs, la
présence d’un arc entre deux nœuds signifiant que l’on peut passer d’un nœud à l’autre. On place sur chaque arc un poids,
représenté par un réel positif, qui représente le coût de passage d’un nœud à l’autre par ce chemin.
En utilisant cette modélisation, il existe de nombreux algorithmes permettant de trouver un plus court chemin dans un
graphe : algorithme de Dijkstra, A*, algorithmes de programmation dynamique etc [1]. La plupart de ces algorithmes
partent d’un nœud de départ et cherchent les nœuds accessibles à partir de ce dernier en suivant les arcs.
Notre application a pour but de trouver le plus court chemin entre la R3 et le CI d’après le graphe présenté sur la figure 1.
3 Conception d’une solution
On va chercher à modéliser le problème en utilisant une conception orientée objet. On ne s’intéresse absolument pas à
l’aspect algorithmique du problème pour l’instant. On propose d’utiliser les classes suivantes pour résoudre le problème :
– une classe Noeud qui modélise les nœuds du graphe ;
– une classe Arc qui modélise les arcs du graphe ;
– une classe Probleme qui modélise un problème particulier, i.e. un graphe avec un nœud de départ et un nœud d’arrivée ;
– une classe Solver qui permet de résoudre des problèmes grâce à un algorithme particulier.
1. dans un premier temps, écrire un diagramme UML représentant les différentes relations qui existent entre ces classes ;
2. affiner ce diagramme en utilisant des navigabilités et visibilités et en proposant une vue plus «implantation »de votre
solution. On supposera que pour les besoins de l’algorithme de résolution, on a besoin étant donné un nœud donné de
connaître les arcs qui partent de ce nœud ;
3. proposer enfin un diagramme de classe UML détaillé faisant apparaître attributs et opérations pour les classes Noeud,
Arc,Probleme et Solver. On supposera que les objets créés n’ont pas besoin d’être modifiés au cours du programme.
Dans ces diagrammes détaillés, on ne fera pas apparaître les éventuels détails d’implantation en ce qui concerne les
multiplicités de type *(choix d’un tableau, d’un objet de type ArrayList etc.). On utilisera la syntaxe UML suivante :
nomAttribut : TypeAttribut [n]
qui précise que nomAttribut est un attribut «contenant »nobjets de type TypeAttribut (cette syntaxe n’impose
pas que cet attribut soit ensuite implanté sous la forme d’un tableau).
Revision b81747b, Wed Oct 31 23:03:40 2012 +0100, Christophe Garion. 1/4

IN201 5 – Algorithme de Dijkstra SUPAERO 2A
Muzak
R3
R2
RU
R1 Foyer Mirage
Machines
`a caf´e
Machines
`a caf´e
CI
Parking
Piscine
2
4
2
31
2
2
1
5
50
4
3
25
3
2
2
25
4
Figure 1 – Où l’on s’aperçoit qu’il ne vaut mieux pas passer par le foyer pour aller en TP d’informatique
2/4

IN201 5 – Algorithme de Dijkstra SUPAERO 2A
4 Implantation de la solution
Vous allez devoir écrire les quatre classes Noeud,Arc,Probleme et Solver et les tester avec JUnit. Toutes les classes
devront appartenir au paquetage fr.supaero.pathfinding. Le solver que vous allez écrire va utiliser l’algorithme de
Dijkstra, présenté ci-dessous sur l’algorithme 4.1. La «fonction »distance permet de trouver la distance minimale du
nœud de départ à un nœud donné et la «fonction »précédent permet de donner pour chaque nœud le nœud précédent
qui assure un plus court chemin.
Algorithme 4.1 : L’algorithme de Dijkstra pour calculer le plus court chemin dans un graphe d’un nœud de départ donné
à un nœud arrivée donné
entrées : un graphe G, un nœud de départ nd et un nœud d’arrivée na
sortie : une séquence Sreprésentant le plus court chemin de nd àna dans le graphe
1noeuds ←ensemble des nœuds du graphe ;
2pour chaque n∈noeuds faire
3distance [n] ← ∞ ;
4pr´ec´edent [n] ←null ;
5fin
6distance [nd ]←0;
7tant que noeuds 6=∅faire
8x←nœud dans noeuds tel que distance [x] est le minimum pour les nœuds appartenant à noeuds ;
9si distance [x]=∞alors
10 retourner null ;
11 fin
12 si x = na alors
13 construire une séquence Sde na ànd en utilisant pr´ec´edent ;
14 retourner S;
15 fin
16 enlever xde noeuds ;
17 pour chaque n∈noeuds tel que xest lié par un arc dànfaire
18 nouvelle distance ←distance [x]+valeur de d;
19 si nouvelle distance <distance [n]alors
20 distance [n]←nouvelle distance ;
21 pr´ec´edent [n]←x;
22 fin
23 fin
24 fin
25 retourner null ;
Un programme applicatif construisant le graphe présenté en figure 1et demandant le plus court chemin entre le nœud «R3 »
et le nœud «CI »vous est fourni sous forme compilée. Une classe de test JUnit de la classe Solver vous est également
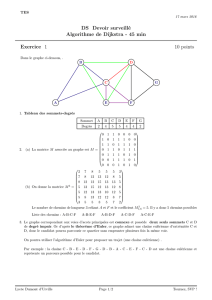
fournie sous forme compilée. Elle utilise le graphe présenté sur la figure 2pour tester votre solution. Les différentes méthodes
de test de la classe vous permettront de mieux cerner les éventuels problèmes de votre algorithme (voir également la javadoc
de la classe).
3/4

IN201 5 – Algorithme de Dijkstra SUPAERO 2A
n1 n2 n3
n4 n5
n6
3
2
1
1
15
1
1
Figure 2 – Le graphe utilisé par la classe de test JUnit de Solver
Pour que tout le monde parte de la même solution, nous vous fournissons le diagramme détaillé de chaque classe. Vous devrez
implanter vos classes (Noeud,Arc,Probleme,Solver) en respectant ces diagrammes si vous voulez que le programme de
test et la classe de test JUnit fournis fonctionnent (n’oubliez pas d’ajouter JUnit comme bibliothèque dans votre projet pour
que les tests fonctionnent). Vous trouverez sur le site les squelettes des classes que vous devez développer sous forme d’un
autre fichier JAR (lisez http://www.tofgarion.net/lectures/IN201/eclipse.php pour comprendre comment importer
des fichiers sources avec Eclipse). Vous disposez également de la classe Solver compilée pour vous permettre d’avancer
dans votre TP. N’oubliez pas d’enlever de votre CLASSPATH ou de votre projet Eclipse l’archive JAR la contenant lorsque
vous allez développer votre propre classe Solver.
Vous pouvez évidemment écrire des spécifications pour préciser le comportement de vos méthodes. Par contre, vous ne
pourrez utiliser ni jmlc ni jmlrac, car nous utilisons les types génériques qui ne sont pas compatibles avec JML.
En ce qui concerne l’implantation de l’algorithme et lui seulement :
– vous devez calculer l’ensemble des nœuds du graphe à partir du problème que vous avez ;
–∞sera représenté par la constante Double.POSITIVE_INFINITY ;
– pour stocker des séquences, on choisira d’utiliser des instances de java.util.ArrayList ;
– pour stocker des ensembles, on choisira d’utiliser des instances de java.util.HashSet. Cette classe s’utilise comme
ArrayList :
– paramètrage de la classe avec le type d’objet contenu (notation java.util.HashSet<Noeud> par exemple)
– méthodes add et remove
– par contre, pas de méthode permettant de retrouver ou de placer un élément à un index particulier comme pour
ArrayList (car il s’agit d’un ensemble)
– les «fonctions »distance et précédent seront codées par des tables de correspondance (ou tableaux associatifs)
représentées en Java par des objets de type java.util.HashMap<K,V> qui est une collection particulière. Dans une
instance de HashMap, on associe des clés de type Kà des valeurs de type V. Pour distance, on aura donc une
HashMap<Noeud,Double> 1et pour précédent une HashMap<Noeud,Noeud>.
La classe HashMap fournit un certain nombre de méthodes utiles :
–put(K key, V value) qui associe l’objet value à la clé key. Si la clé a déjà été utilisée, l’objet associé est remplacé
par le nouvel objet
–get(K key) qui renvoie un objet de type Vcorrespond à la clé key
La documentation javadoc de la classe sur le site de Oracle [2] vous fournira plus de détails.
5 Travail à rendre
Vous avez plusieurs documents à rendre :
– lorsque vous avez fini votre conception sur papier, vous la remettez à votre PC(wo)man avant d’aller en TP ;
– à la fin de la séance, vous renvoyez vos classes à votre PC(wo)man ;
– vous renvoyez le TP complet (sans les diagrammes de conception) jeudi soir.
Références
[1] T.H. Cormen et al. Introduction à l’algorithmique. 2eéd. Dunod, 2004.
[2] Java API specifications.url :http://download.oracle.com/javase/6/docs/api/index.html.
1. Double est une classe représentant des réels. Elle permet d’encapsuler le type primitif double dans des objets.
4/4