TP n 12 – Représentations graphiques et applications

Lycée Jean Bart – PCSI – Année 2013-2014 – 8 & 15 avril 2014
TP n012 – Représentations graphiques et
applications
Objectifs du TP
Le but de cette séance est de commencer à vous faire découvrir les différentes représentations graphiques réa-
lisables grâce à Python, pour pouvoir les appliquer dans un proche avenir à des problèmes issus de situations
concrètes (par exemple : résolution d’équations différentielles par la méthode d’Euler).
Comme toujours, n’oubliez pas de sauvegarder votre travail. Par ailleurs, vous aurez besoin lors de cette séance de
télécharger des fichiers sur le site, dont voici l’adresse : www.pcsijbmath.sitew.fr.
1. Graphiques en Python : la bibliothèque matplotlib
Le but de cette section est de vous familiariser avec les représentations graphiques à l’aide de Python. Comme
vous vous en doutez sûrement, il est possible de créer avec Python les mêmes types de graphiques que votre calcu-
latrice (eg courbe représentative d’une fonction, histogramme, etc. . . ) mais aussi d’autres variétés de diagrammes
que vous avez déjà rencontrés cette année ou que vous serez amenés à utiliser prochainement (eg portrait de phase,
champ de vecteurs, représentations graphiques 3D).
Comme vous vous en doutez aussi, les fonctions permettant de générer un graphique en Python sont contenues dans
une bibliothèque, poétiquement nommée matplotlib ∗. Plus précisément, la bibliothèque matplotlib est tellement
vaste que nous nous servirons dans un premier temps que d’une partie, une sous-bibliothèque appelée †pyplot .
Pour pouvoir utiliser les fonctions de cette bibliothèque, il convient en premier lieu de l’importer. Cela se fait
comme d’habitude par le biais de la commande “import”, avec une petite variante cependant :
import matplotlib.pyplot as plt
Toutes les fonctions contenues dans “pyplot” doivent a priori être précédées de “matplotlib.pyplot” pour être
utilisées. . . ce qui rend la syntaxe extrêmement lourde. Pour l’alléger, le “as plt” de la ligne ci-dessus permet de
remplacer “matplotlib.pyplot” par “plt”. Un petit dessin valant mieux qu’un long discours, voici un premier exemple
de graphique en Python :
Décryptons rapidement ces instructions :
äplt.axis définit la fenêtre d’affichage ‡. Sa syntaxe est : plt.axis([Xmin, Xmax, Ymin, Ymax,])
äplt.plot permet de tracer un nuage de points, dont on donne la liste des abscisses puis la liste des ordonnées.
L’instruction ’ro’ en fin de commande correspond à la couleur (’r’ pour rouge) et au style des points (’o’
pour un joli rond). Les autres couleurs disponibles sont par exemple :
∗. Un peu “d’étymologie informatique” : “mat” comme maths ; “plot” comme tracé (notons au passage que le mot “plot” a une
incroyable quantité de sens possibles en anglais suivant le contexte) ; et “lib” comme library qui signifie bibliothèque.
†. Non moins poétiquement que précédemment.
‡. Comme le “range” de votre calculatrice.

2PCSI — Année 2013-2014 — Informatique: TP — 8 & 15 avril 2014
+b pour bleu ;
+g pour vert ;
+c pour cyan ;
+m pour magenta ;
+y pour jaune ;
+k pour noir ;
+w pour blanc §.
Dans l’hypothèse où ces couleurs ne vous suffiraient pas, vous pouvez les définir en RGB, c’est-à-dire sur 3
octets écrits en hexadécimal via l’instruction : macouleur = ’#ee01f8’. Le rouge correspond alors au code
’#ff0000’, le vert au code ’#00ff00’ et le bleu ’#0000ff’. Pour des exemples plus nuancés, consulter sur le
web n’importe quelle palette de couleurs RGB.
Quant au style des points, on peut donc choisir des ronds avec ’o’, des croix droites avec des ’+’ ou des ’x’.
äplt.show permet comme son nom le suggère d’afficher le graphique créé.
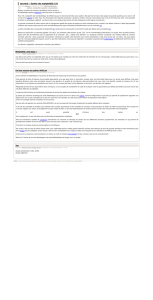
Pour aller un peu plus loin dans la description des possibilités graphiques de cette bibliothèque, voici un exemple
plus consistant (le fichier source est téléchargeable sur le site).
§. A éviter sur un fond blanc.

PCSI — Année 2013-2014 — Informatique: TP — 8 & 15 avril 2014 3
Exercice 1. — Télécharger sur le site le fichier source de l’exemple ci-dessus (appelé exemple2.py), et vous
l’approprier. . . C’est-à-dire essayer de modifier les différents paramètres (couleur, dimensions de la fenêtre, style
des points, listes des abscisses, légendes. . . ) pour comprendre l’utilité de chaque instruction de ce petit programme.
Exercice 2. — Maintenant que vous maîtrisez tous les paramètres de pyplot, tracer, sur le même graphique :
a) la courbe représentative de la fonction cosinus, sur [0,3], avec un pas de 0,1 ;
b) la courbe représentative de la fonction inverse, sur [1,5], avec un pas de 0,2 ;
c) la courbe représentative de la fonction exponentielle, sur [0,4], avec un pas de 0,01 ;

4PCSI — Année 2013-2014 — Informatique: TP — 8 & 15 avril 2014
Exercice 3. — (Nuages de points). Ecrire un programme demandant à l’utilisateur :
1) les coordonnées de 3 points, et qui place ces trois points dans un graphique.
2) un entier N, les coordonnées de Npoints, et qui place ces trois points dans un graphique.
Exercice 4. — (Mouvement brownien). Il s’agit ici de modéliser le mouvement aléatoire d’une particule
en suspension dans un fluide, appelé mouvement brownien. La modélisation proposée est la suivante :
äA l’étape 0: la particule (le point) a pour co-
ordonnées (0,0) (tant qu’à choisir une origine
dans le plan, autant qu’elle facilite les calculs
ultérieurs).
äDe l’étape nà l’étape n+ 1 : la particule
parcourt un segment de longueur 1, dans une
direction formant un angle aléatoire θn(com-
pris entre 0et 2π) avec l’axe (Ox).
äLe nombre d’étapes (donc de segments par-
courus par la particule) sera un entier Nsaisi
au clavier par l’utilisateur.
2. Approximation aux moindres carrés : droite de régression
Nous avons vu en cours sur un exemple comment détermi-
ner la droite approchant “au mieux” (au sens des moindres
carrés) les 3 points du plan de coordonnées (0,0),(1,1) et
(2,1).¶
Le but est de généraliser cette construction, et de construire
un programme donnant la droite de régression (“y=ax +b”)
pour un nuage de points quelconques du plan. Pour cela, il
“suffit” de généraliser les calculs vus en cours à un nombre
de points quelconques, et d’obtenir aet ben traduisant la
nullité d’un produit scalaire.
Dans l’hypothèse où vous ne sauriez pas comment faire pour y parvenir, voici un énoncé utile :
Propriété — Soit (xi, yi)i=1,...,n un nauge de npoints du plan. La droite de régression de ce
nuage de points a pour équation y=ax +b, où aet bsont solutions du système :
(n
∑
i=1
xi)a+nb =
n
∑
i=1
yi
a(n
∑
i=1
x2
i)x+b(n
∑
i=1
xi)=
n
∑
i=1
xiyi
Exercice 5. — A l’aide de cette propriété, écrire un programme construisant la droite de régression associée
à un nuage de npoints du plan (nétant choisi par l’utilisateur), et faisant apparaître sur le même graphique le
nuage de points et la droite de régression. Ce travail pourra être décomposé en plusieurs étapes, par exemple :
äSaisie de n, et des coordonnées des npoints ;
äCalcul des différentes sommes intervenant dans le système de la propriété ci-dessus ;
äRésolution du système (utilisez ce que vous avez déjà fait !) ;
äGraphiques.