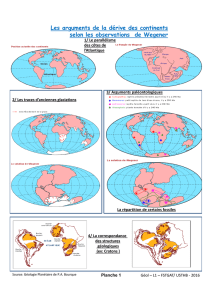
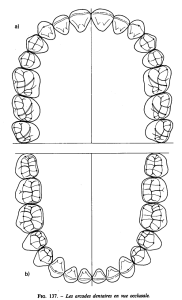
ENS option MP

ENS option MP
Planche 1 Informatique
Soit A un alphabet (fini).
Montrer que {ww, w ∈A∗}n’est pas rationnel.
Soit B= (Q, q0, F, δ) un automate fini d´eterministe complet (δest une fonction de Q×Adans
Q). Pour tout mot wde A∗, on note fwla fonction de Qdans Qd´efinie par fw(q) = δ(q, w).
Soient Lun langage rationnel et fune fonction de Qdans Q.
Montrer que Lf={w, fw=f}est rationnel.
Montrer que R(L) = {w, ww ∈L}est rationnel.
Montrer que S(L) = {w, w|w|∈L}est rationnel.
Montrer que T(L) = {w, w2|w|∈L}est rationnel.
On dit qu’un sous-ensemble Ede Nest hh parfaitement p´eriodique ii s’il existe n0et pdans Ntels
que pour tout n>n0,n+p∈E⇔n∈E.
`
A l’aide de cette notion, g´en´eraliser (montrer, par exemple, que U(L) = {w, w22|w|∈L}est
rationnel).
Planche 2 Ulm - Lyon - Cachan
Soient Fune application de classe C1sur Rn, `a valeurs dans Rn,Let Pdeux applications de
classe C1sur R`a valeurs dans Mn(C), telles que ∀x∈Rn, dL(x)F(x)=L(x)P(x)−P(x)L(x).
Soit x, d´efinie sur R`a valeurs dans Rn, la solution de l’´equation diff´erentielle x0(t) = Fx(t)
avec, pour condition initiale, x(t0) = x0.
Montrer que ∀k∈N,trLx(t)k est constant.
Montrer que le spectre de Lx(t)ne d´epend pas de t.
Planche 3 Ulm - Lyon - Cachan
Soit n>1. On munira Mn(C) d’une norme judicieusement choisie. Montrer que ∃r > 0,∃C > 0,
tels que, pour tout couple (A, B) de matrices inversibles, si kA−Ink6ret kB−Ink6r,
alors 
ABA−1B−1−In 6CkA−Ink.kB−Ink.
On dit qu’un sous-groupe Gde GLn(C) est discret si, pour tout lde G, il existe ε > 0 tel que
G∩B(l, ε) = {l}.
Soient Aet Bdeux matrices inversibles non permutables, telles que Asoit diagonalisable `a
valeurs propres simples et ∃r > 0, kA−Ink6ret kB−Ink6r. D´eduire de la question
pr´ec´edente que si rest assez petit, le groupe engendr´e par Aet Bn’est pas discret.
Planche 4 Ulm - Lyon - Cachan
On donne un entier n>0 et, dans I=[0,1],n+ 1 points distincts x0, . . . , xn. Si fest continue
de Idans R, on d´esigne par kfk∞la borne sup´erieure de fsur I.
Montrer que, si fet ε > 0 sont donn´es, il existe un polynˆome Q∈R[X] tel que kf−Qk∞6ε
et ∀`∈ {0, . . . , n}, f(x`) = Q(x`).
Donner des exemples de sous-espace vectoriels de Mn(R) dont seul l’´el´ement nul soit diagonal-
isable. Peut-on en majorer la dimension ?
Planche 5 Ulm Lyon - Cachan
Que peut-on dire des matrices sym´etriques ?
Soient Aet Bsym´etriques d’ordre n, de valeurs propres respectives (λi) et (µi).
Montrer que
n
X
i=1
(λi−µi)26tr(A−B)2.
Planche 6 Ulm Lyon - Cachan
Montrer que si Aest carr´ee d’ordre 2, r´eelle et de trace nulle, il existe Bde diagonale nulle
orthogonalement semblable `a A.
Montrer cette propri´et´e dans le cas g´en´eral (on pourra utiliser f(M) = max
i,j (mii −mjj )).
L’officiel de la taupe num´ero  Page c MMXII ´ Editions Officiel de la Taupe

Planche Sup 7 Ulm
On note Gnl’ensemble des polynˆomes de Cn−1[X] de terme constant nul et de coefficient du
terme de degr´e 1 non-nul.
Pour tout (P, Q)∈G2
n, montrer qu’il existe un unique polynˆome P∗Qtel que Xndivise
P◦Q−P∗Q.
Montrer que (Gn,∗) est un groupe.
Soit Nune matrice nilpotente de taille n; montrer que, pour tout l∈N∗, il existe Nlnilpotente
de taille ntelle que (In+Nl)l=In+N. Montrer que Nltend vers 0 quand ltend vers +∞.
Planche 8 Ulm
Soit Gun sous-groupe ab´elien de SLn(C).
Montrer que l’adh´erence Gde Gest un sous-groupe ab´elien.
Caract´eriser Glorsque Gest un sous-groupe monog`ene de SLn(C).
Planche 9 Lyon
Si pest continue de Rdans Ret int´egrable sur R+, montrer que y00 +py = 0 admet des solutions
non born´ees.
Planche 10 Lyon
On donne l’´equation diff´erentielle y0=y2−x; ´etudier la solution maximale (I, φ) du probl`eme
de Cauchy (x0, y0) avec x0>0 et |y0|6√x0; on montrera que sup I= +∞, que inf I∈R, que
φtend vers −∞ en sup Iet inf I.
Tracer l’allure g´en´erale d’une telle solution.
Montrer qu’il n’existe pas ε > 0 tel que φ(x)>ε−√xpour xassez grand.
Planche 11 Lyon
Pour P∈C[X] et r > 0, montrer que m(r) = sup
|z|6r|P(z)|est atteint en un point de module r.
Planche Sup 12 Lyon
Soit fcontinue, positive et born´ee de Rdans R.
On note mf(x, t) = 1
2tZx+t
x−t
f(u)duet Mf(x) = sup
t>0
mf(x, t).
Montrer que f(x)6Mf(x)6sup
x∈R
f(x).
Montrer que si fest uniform´ement continue, Mfl’est aussi.
Montrer que si fest continue, Mfl’est aussi
Planche Sup 13 Cachan
Que dire des solutions de u00 =−favec u(0) = u(1) = 0, o`u f∈ C0([0,1],R) ?
Soient N∈Net h=1
N+ 1 ;∀nde [1, N], on pose Fn=f(nh). On note Fle vecteur de
coordonn´ees Fnet u, de coordonn´ees (u1, . . . , uN) v´erifiant :
∀n∈[1, N],(H)−1
h2(un+1 −2un+un−1) = Fn,u0=uN+1 = 0.
Donner le rapport avec les solutions de l’´equation diff´erentielle et trouver u.
Mettre (H) sous la forme Au =F, o`u Aest une matrice carr´ee.
Montrer que si AX est `a coefficients n´egatifs, alors Xl’est aussi, puis en d´eduire que Aest
inversible et que les coefficients αij de Asont positifs et v´erifient 0 <X
i,j
αij 61
8·
L’officiel de la taupe num´ero  Page c MMXII ´ Editions Officiel de la Taupe

Planche 14 Cachan
Le but de l’exercice est de montrer qu’une fonction continue sur une partie convexe compacte C
d’un espace vectoriel E, `a valeurs dans C, admet un point fixe.
On choisit d’abord E=Rn, et Cla boule unit´e ferm´ee centr´ee en 0.
En supposant que l’on dispose d’un th´eor`eme du point fixe pour toute fonction C1, continue de
B(0,1) ferm´ee dans B(0,1−ε) ferm´ee (pour tout ε > 0), montrer qu’il en est de mˆeme pour une
fonction C1, continue de B(0,1) ferm´ee dans B(0,1) ferm´ee.
Montrer que l’on peut g´en´eraliser aux fonctions seulement continues.
Montrer que l’on peut g´en´eraliser `a un compact convexe.
Planche 15 Cachan
Soit Aune matrice de taille nantisym´etrique r´eelle. Montrer que les solutions de X0=AX
vivent dans un espace affine dirig´e par l’image de Aet qu’elles ont une norme constante.
On choisit n= 3 : montrer que les solutions parcourent des cercles (en entier).
Planche 16 Cachan
Pour z0donn´e dans C, on d´efinit une suite (zn) par zn+1 =z2
n+co`u c∈C. Montrer que l’ensemble
Kcdes complexes z0tels que la suite (zn) soit born´ee est compact (on pourra montrer dans un
premier temps que si |z0|>2 + |c|la suite (|zn|) tend vers +∞).
ENS option PC
Planche 17
Volume de Sn={(x1, . . . , xn)∈Rn, xi>0,
n
X
i=1
xi<1}.
Planche Sup 18
Soit P∈R[X] non constant ; montrer que si aest racine multiple de P, alors aest racine de P0.
Trouver tous les P∈R[X] tels que ∀x∈R, P (x)P00(x)6P02(x).
Planche 19 Ulm - Lyon
Caract´eriser l’ensemble Edes matrices sym´etriques et positives.
Soit uune application de classe C1sur R`a valeurs dans E.
Montrer que, si tr(u0+u2)>0, alors ∃(a, b)∈R∗2
+tel que ∀t∈R, l’une des valeurs propres λ(t)
de u(t) est sup´erieure ou ´egale `a a
b+t·
Imaginer une application utelle que l’une au moins des valeurs propres de u(t) soit plus petite
que a
b+t·
Planche 20 Ulm - Lyon
On d´efinit fde classe C1sur R2par f(x, y) = x&yo`u & est une loi associative, poss`ede un
neutre not´e e, et pour laquelle tout ´el´ement est inversible.
Montrer qu’il existe un C1-diff´eomorphisme φde Rdans R, tel que φ(x&y) = φ(x) + φ(y) (on
pourra supposer que φexiste et on cherchera `a l’exprimer en fonction de f).
Planche Sup 21 Ulm - Lyon
On dit qu’une famille Fde vecteurs d’un R-espace vectoriel Ede dimension finie n>1, est en
position g´en´erale, si toute famille de nvecteurs distincts de Fest une base de E.
Donner un exemple de famille infinie en position g´en´erale sur R2puis sur Rn.Rnpeut-il se
d´ecomposer comme r´eunion finie d’hyperplans ?
Planche 22 Lyon - Cachan
Montrer que h, born´ee et de classe C1de R2dans R, telle que ∃(a, b)∈R2,∀(x, y)∈R2, h(x, y) = a∂h
∂x +b∂h ∂y ,
est nulle.
Que se passe-t-il si on remplace aet bpar des fonctions de xet y?
L’officiel de la taupe num´ero  Page c MMXII ´ Editions Officiel de la Taupe

Planche 23 Lyon - Cachan
Soient uet φde classe C1de Rdans C, 2π-p´eriodiques. Montrer que l’´equation v(x)−z
2πZ2π
0
u(x−t)v(t)dt=φ(x)
admet une unique solution pour chaque zpris dans un ensemble `a d´eterminer.
Planche 24 Lyon
Soit φde classe C∞de Rdans Rdont toutes les d´eriv´ees successives sont born´ees. Donner la
limite en +∞de I(λ) = Z+∞
−∞
e−λx2φ(x)dx.
En donner un ´equivalent en +∞et un d´eveloppement asymptotique.
´
Ecole Polytechnique option MP
Planche 25
I) Soit Aune matrice sym´etrique r´eelle d’ordre net Wun sous-espace de Rnde dimension ktel
que pour ∀w∈W, twAw > 0. Montrer que Aa au moins kvaleurs propres strictement positives.
Soit Aune matrice sym´etrique r´eelle d’ordre n. Montrer l’´equivalence entre les deux propositions
suivantes :
Aest d´efinie positive.
Tous les mineurs principaux de A(les d´eterminants des sous-matrices carr´ees extraites de Aen
gardant les mˆemes indices de ligne et de colonne) sont strictement positifs.
II) Soit (un) une suite d´efinie par r´ecurrence : u0et u1sont dans Z/pZ(pentier naturel
quelconque), et ∀n, un+2 = 2un+1 +un(les op´erations d’addition et de multiplication se font
donc dans Z/pZ). Cette suite peut-ˆetre ˆetre p´eriodique ?
Planche Sup 26
On consid`ere la suite de Fibonacci d´efinie par u0= 0, u1= 1 et un+1 =un+un−1pour n>1.
D´eterminer unen fonction de n.
Montrer que, pour (n, p)∈N2, on a p|n⇒up|un.
Montrer que, pour (p, q)∈N2, on a up∧q=up∧uq.
Planche Sup 27
I) Soient nmatrices A1, . . . , Ande GLn(Z), S={A1, . . . , Ak}; on suppose que ∀i∈[1, n], AiS=S.
Montrer que trk
X
i=1
Ai≡0 [k].
Soit Gun groupe multiplicatif fini de Mn(R).
Montrer que si trX
A∈G
A= 0, alors X
A∈G
A= 0.
II) Montrer que l’´equation xn+nx = 1 admet une solution unique xn∈R∗; trouver la limite
et un ´equivalent de (xn).
Donner la nature de la s´erie X
n>0
n!1
n−xn.
Planche 28
Soit Aune partie de C. Pour n>1, on note Pn,A l’ensemble des polynˆomes unitaires de degr´e
n`a racines dans A.
Pour z /∈A, minorer {|P(z)|, P ∈Pn,A}.
Montrer que si Aest ferm´ee, Pn,A l’est aussi.
Que dire de Pn,A si Aest compacte ? Ouverte ?
Planche 29
I) Soit Qune forme quadratique, et φla forme polaire associ´ee. Trouver une condition n´ecessaire
et suffisante pour que le cˆone isotrope de Qsoit ´egal au noyau de φ.
II) Soit Aune matrice sym´etrique telle que ses coefficients diagonaux soient ses valeurs propres.
Montrer que Aest diagonale.
L’officiel de la taupe num´ero  Page c MMXII ´ Editions Officiel de la Taupe

Planche Sup 30
On dit qu’une suite (un) est hh presque de Cauchy ii si :
∀ε > 0,∃N∈N,∀n > N, |un+1 −un|< ε.
Trouver une suite presque de Cauchy qui ne soit pas de Cauchy.
Soient Iun intervalle de R, (an) et (bn) deux suites de Itelles que lim
n→+∞|an−bn|= 0. Montrer
qu’il existe une suite (xn) presque de Cauchy, telle que ∀k∈N,∃j∈N,(ak, bk) = (xj, xj+1).
Montrer que f, de Idans R, est uniform´ement continue si et seulement si elle transforme toute
suite presque de Cauchy en une suite presque de Cauchy.
Si, de plus, Iest born´e, montrer que fest uniform´ement continue si et seulement si elle transforme
toute suite de Cauchy en une suite presque de Cauchy.
Donner un exemple de fonction continue mais pas uniform´ement continue.
Montrer que la fonction hh racine ii est uniform´ement continue sur R+.
Construire une suite presque de Cauchy dont l’ensemble des valeurs d’adh´erence soit Rtout
entier.
Montrer que l’ensemble des valeurs d’adh´erence d’une suite presque de Cauchy est un intervalle.
Planche 31
I) On note Sla sph`ere unit´e de R3,A1,...An,B1,...Bn,C1,...Cn, des points de S.
Montrer qu’il existe P∈Stel que
n
X
k=1
P A2
k=
n
X
k=1
P B2
k=
n
X
k=1
P C2
k.
Quel est l’ensemble des solutions possibles dans chaque cas ?
II) Montrer que f, d´efini sur Ω = {(x, y)∈R2, x2+y2>1}par f(x, y) = 1
2x+x
x2+y2, y−y x2+y2,
est un C1-diff´eomorphisme et d´eterminer son image.
Planche 32
Montrer que, si (Sn) est une suite de matrices de Mn(K), commutant 2 `a 2 et toutes nilpotentes,
il existe un vecteur Xnon nul v´erifiant ∀n∈N, SnX= 0.
Soit (Sn) une suite de matrices de Mn(K), commutant 2 `a 2 et qui poss`edent un vecteur propre
commun ; montrer qu’il existe un vecteur propre commun a la suite (tSn).
Planche 33
I) Donner la nature de la s´erie de terme g´en´eral f(n), o`u fest C1de [1,+∞[dans R∗
+et telle
que lim
t→+∞
f0(t)
f(t)=−∞.
Donner un ´equivalent du reste de la s´erie.
II) Que dire d’une matrice Atelle que, pour toute matrice Pinversible, P A est sym´etrique ?
Planche 34
I) Pour n∈N∗, on note a(n) le plus grand diviseur premier de n. Donner la nature de X1
na(n)·
II) On dit que deux permutations de Sn,c1et c2sont conjugu´ees, s’il existe une permutation s
telle que c1=s◦c2◦s−1.
Soient c1et c2deux cycles, P1et P2leurs matrices associ´ees ; montrer que c1et c2sont conjugu´es
si et seulement si P1et P2sont ´equivalentes.
Mˆeme question si c1et c2sont deux permutations quelconques.
Planche Sup 35
I) On note u, v, w les racines de X3+pX +q∈C[X] ; trouver le polynˆome unitaire de degr´e
minimal dont u2+v2,v2+w2, et w2+u2sont les racines.
II) R´esoudre dans M2(R), X2=0−1
1 0 .
L’officiel de la taupe num´ero  Page c MMXII ´ Editions Officiel de la Taupe