Chapitre 6 LE POTENTIEL PERIODIQUE

Chapitre 6
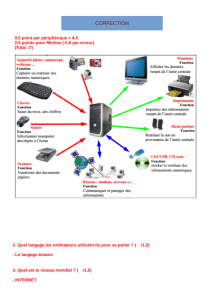
LE POTENTIEL PÉRIODIQUE
6.1 Le double puits de potentiel
Considérons une particule de masse msoumise à l’énergie potentielle V(x)dont
le graphe est représenté sur la Þgure 6-1.
Figure 6-1.
Si dest assez grand, chacun des puits peut être étudié indépendamment de l’autre.
Les puits étant identiques, ils présentent des spectres d’énergie identiques. Soit El’une
des valeurs du spectre. Une particule piégée dans le premier puits avec l’énergie Eapour
fonction d’onde u1(x).La particule piégée dans le second puits avec la même énergie E
est décrite par la fonction d’onde u2(x).Les fonctions u1et u2représentent deux états de
même énergie. Elles se déduisent de l’étude générale des fonctions uE(x)du paragraphe
5.2. Les densités de présence, ρ1et ρ2,correspondant à deux solution de même énergie E,
sont représentées sur la Þgure 6-1. Toute combinaison linéaire de u1et u2est une fonction
propre de l’hamiltonien ˆ Hpour la valeur propre E. Cette valeur propre se trouve donc
dégénérée d’ordre 2†.
Lorsque la distance 2d, entre les deux puits diminue le potentiel se présente sous
la forme d’un puits de potentiel unique présentant en son milieu une barrière de potentiel
(voir la Þgure 6-2 a). Nous assimilons cette barrière de potentiel à la fonction W0δ(x)où
l’on a posé W0=Rd+ε
−d−εV(x)dx =2dV
0,tandis que δ(x)est la fonction généralisée de
Dirac.
†Les résultats généraux du paragraphe 5.3 page 74 ne sont pas remis en cause car, en toute rigueur, il
n’y a dégénérescence que pour d→∞.

78 Le potentiel périodique
a a
x
Vx()
- a a
x
EE
∞∞
W x
0
δ
()
a) b)
V
0
Figure 6-2.
Nous considérons le cas où l’énergie Esatisfait la relation 0<E<<V
0.Dans
ces conditions, par souci de simpliÞcation, nous admettons que V0est pratiquement inÞni.
L’énergie potentielle est alors la fonction V(x)de la Þgure 6-2 b),telle que
V(x)=½∞pour |x|>a
W0δ(x)pour |x|<a
Soit uE(x)une fonction propre de l’hamiltonien pour la valeur propre E. La
fonction uEsatisfait l’équation
−~2
2mu00
E(x)+V(x)uE(x)=Eu
E(x)(6.1)
Les conditions de continuité en x=±aimposent la condition uE(±a)=0.
Aucune condition de continuité n’est imposée sur la dérivée de uEpour les raisons déjà
évoquées page 35 (§2).
En x=0on impose la continuité de la fonction uE.Pour obtenir la condition
imposée sur la dérivée de uEon intègre l’équation 6.1 entre −εet εoù εest une quantité
positive arbitrairement petite :
−~2
2m(u0
E(ε)−u0 E(−ε)) + W0uE(0) = 0 ⇒u0 E(ε)−u0 E(−ε)=2mW0
~2uE(0) (6.2)
Les solutions de l’équation 6.1 s’écrivent sous la forme
uE(x)=
0pour |x|>a
uI(x)pour −a<x<0
uII (x)pour 0<x<a
avec
uI(x)=Aeikx +Be−ikx
uII (x)=Ceikx +De−ikx (6.3)
où l’on a posé k:= √2mE
~,tandis que A, B, C et Dsont des constantes arbitraires, reliées
entre elles par les conditions de passage.
La fonction δ(x)est une fonction paire, par conséquent l’opérateur parité com-
mute avec l’hamiltonien. Nous cherchons donc les fonctions uEqui sont soit paires soit
impaires.

Le double puits de potentiel 79
Solutions impaires : αet ϕétant des constantes arbitraires, nous posons
uII (x)=αsin (kx +ϕ),ce qui est l’expression la plus générale de uII (x),écrite sous une
forme différente de l’expression 6.3. La fonction cherchée étant impaire, on en déduit par
symétrie uI(x)=αsin (kx −ϕ)
Lesconditionsdecontinuitéenx=±as’écrivent sin (ka +ϕ)=0.En x=0,il
vient
uII (0) = αsin (ϕ)=uI(x)=αsin (−ϕ)
On peut donc poser ϕ=0,la constante αétant de signe arbitraire. On vériÞe alors que
la condition 6.2 est satisfaite.
Ainsi la solution cherchée est de la forme
uE=αisin (kx)pour −a<x<aavec
sin (ka)=0
Le coefficient constant est ici noté αi.
De la relation sin (ka)=0on déduit les valeurs possibles de Eassociées aux
solutions impaires de l’équation aux valeurs propres de l’hamiltonien : Eni=n2×π2~2
2ma2
où nest un entier arbitraire.
Solutionspaires: Nous posons ici uII (x)=αcos (kx +ϕ)et, pour des raisons de
parité, uI(x)=αcos (kx −ϕ).On peut toujours considérer que ϕappartient à l’in-
tervalle [−π/2,π/2] et que αest une constante arbitraire car deux fonctions d’ondes
proportionnelles décrivent le même état physique.
Lesconditionsdecontinuitéenx=±as’écrivent : cos (ka +ϕ)=0.Les condi-
tions de continuité en x=0s’écrivent u0
II (0) −u0 I(0) = 2mW0
~2uE(0) ,soit
−2αk sin ϕ=2mW0
~2αcos ϕ. On obtient
tan ϕ=−mW0
~2k
Supposons la relation mW0
~2k>> 1.On en déduit ϕ'−π/2,plus précisément ϕ=−π
2+θ
avec θ<<π.
tan θ=~2k
mW0
'θ
et donc
uI(x)=−αpsin (kx −θ),u
II (x)=αpsin (kx +θ)avec
sin (ka +θ)=0
Ici, la constante αest notée αp.
De la relation sin (ka +θ)=0,on déduit Enp =n2×π2~2
2ma2µ1−2θ nπ ¶où
nous avons négligé les termes de l’ordre de θ2.Dans les mêmes conditions on trouve
θ=nπ~2
maW0
et Enp=n2×π2~2
2ma2µ1−2~2 maW0¶

80 Le potentiel périodique
E
p
E
i
u
1paire
u
1impaire
x
x
a
)
b
)
-a a
-a a
Figure 6-3.
Le spectre de l’hamiltonien est représenté sur la Þgure 6-3 a). Pour les solutions
impaires, le spectre est celui du puits inÞni. C’est presque le même spectre pour les
solutions paires ; cependant, la dégénérescence qui serait présente pour θ=0est levée
(θ=0signiÞeW0=∞ou encore d=∞).
Sur la Þgure 6-3 b) nous avons représenté les fonctions u1paire et u1impaire,fonctions
d’onde paire et impaire de plus basse énergie (n=1)pour αp=αi,en supposant θ
négligeable.
Considérons le cas où la particule est initialement décrite, à l’instant t=0,par
la fonction d’onde ψ0=u1paire +u1impaire.Au cours du temps ψ0évolue :
ψ(t, x)=e−iE1pt/~u1paire (x)+e−iE1it/~u1impaire (x)
=e−iE1it/~³e−i(E1p−E1i)t/~u1paire (x)+u1impaire (x)´.
Il est toujours loisible de multiplier la fonction d’onde par une constante (indé-
pendante de x); la nouvelle fonction d’onde ainsi obtenue décrit le même état physique.
Nous considérons donc la fonction d’onde
Ψ(t, x)=eiΩtu1paire (x)+u1impaire (x)(6.4)
avec ~Ω=(E1i−E1p)=n2π2~4
2m2a3W0
avec, ici, n=1A l’instant t=π/Ωla fonction
d’onde est Ψ=−u1paire (x)+u1impaire (x).
Les fonctions Ψ(0,x)et Ψ(π/Ω,x)sont représentées sur la Þgure 6-4 pour αp=
αi:
Ψ(0,x)=u1paire (x)+u1impaire (x)et Ψ(π/Ω,x)=−u1paire (x)+u1impaire (x)
Figure 6-4.

Le double puits de potentiel 81
Initialement la particule est dans le puits de droite. La théorie classique prédit
que la particule reste à droite car elle ne peut pas traverser la barrière W0δ(x)qui est
inÞniment haute. La théorie quantique prévoit que la particule peut passer dans le puits
de gauche par effet tunnel. C’est effectivement ce qui se passe. On vériÞe aisément que la
fonction d’onde 6.4 est une fonction périodique de période 2π/Ω.Le passage d’un puits à
l’autre s’effectue en un temps π
Ω=πθ ~2 ma2.
Le modèle précédent décrit qualitativement la molécule d’ammoniac NH3.
H
HH
N
Vx()
x
Figure 6-5.
Dans la position d’équilibre stable, les trois noyaux d’hydrogène, H, forment un
triangle équilatéral qui déÞnit un plan P. Par raison de symétrie, la théorie classique
prévoit l’existence de deux positions d’équilibre stables sur axe perpendiculaire à P, de
part et d’autre de P. Cette propriété se traduit par l’existence de deux puits de potentiel
séparés par une barrière dans le plan P.
La fréquence d’oscillation par effet tunnel d’une position d’équilibre à l’autre est
une caractéristique de la molécule d’ammoniac. Celle-ci peut donc servir de référence pour
asservir un oscillateur micro-ondes qui déÞnit un étalon de temps précis.
Considérons de nouveau la Þgure 6-1. Le cas particulier qui vient d’être étudié
conduit aux résultats suivants. Lorsque d=∞(c’est à dire θ=0)les spectres de l’énergie
des solutions paires et impaires sont les mêmes. Par contre, la dégénérescence se lève
lorsque ddécroît (c’est à dire lorsque la barrière devient quelque peu transparente).