UFR Sciences

Les trois exercices sont indépendants. Documents interdits. Calculatrice autorisée.
I - Recherche d’exoplanètes
Partie A : préambule
On considère un ensemble de deux corps célestes assimilés à des points matériels 𝐸 et 𝑃, de
masses respectives 𝑀 et 𝑚 et de centre de masse 𝐺. On suppose que ce couple est isolé et qu’il ne
subit aucune interaction extérieure. On note 𝑟=𝐸𝑃 la distance relative entre les deux corps.
1) Rappeler l’expression de la force de gravitationnelle 𝐹
!→! exercée par le corps de masse 𝑀
sur le corps de masse 𝑚 ? Faire un dessin.
𝐹
!→!=−𝒢"#
!!𝑟
2) Écrire les équations du mouvement satisfaites par chacun des deux corps dans un référentiel
galiléen d’origine 𝑂. En déduire le mouvement du centre de masse 𝐺 dans ce référentiel. Que
peut-on dire du référentiel barycentrique 𝑅∗ ?
𝑀!!!"
!!!=!𝐹
!→! et 𝑚!!!"
!!!=!𝐹
!→! avec 𝐹 !→!=−𝐹 !→!. On en déduit que !!!"
!!!=0 et
donc que le centre de masse 𝐺 est immobile ou a un mouvement rectiligne uniforme par
rapport à 𝑂.
𝑅∗ est galiléen.
3) Déterminer les positions 𝐺𝐸 et 𝐺𝑃 des deux corps par rapport à leur centre de masse 𝐺 en
fonction de 𝑟 ? En déduire les vitesse𝑠!𝑣! et 𝑣! des deux corps dans 𝑅∗ en fonction de 𝑣=!!
!" .
𝐺𝐸 =−!
!!!
𝑟 et 𝐺𝑃 =!
!!!
𝑟.
𝑣!=−!
!!!
𝑣 et 𝑣!=!
!!!
𝑣.
4) Il est possible d’étudier le mouvement relatif des deux corps à partir de l’équation du
mouvement dans le référentiel barycentrique 𝑅∗ d’un point matériel virtuel 𝑉. Donner cette
équation sans la démontrer et préciser la masse, la position et la vitesse de ce point matériel 𝑉.
𝜇!!
!"
=𝐹
!→! avec 𝜇=!"
!!!. La position de V est définie par 𝑟 et sa vitesse, par 𝑣.
On supposera dans la suite que la trajectoire de 𝑉 dans 𝑅∗ est circulaire.
5) Rappeler l'expression de l'accélération du point matériel virtuel 𝑉 dans la base intrinsèque ou
dans la base polaire pour un mouvement circulaire. En déduire que la norme de la vitesse de
𝑉 est une constante et que la relation entre la période de rotation T de ce point et la distance 𝑟
s’écrit
ANNÉE 2015-2016
Examen terminal 1ère session
16 décembre 2015
LICENCE Sciences et Technologie – 2ème année
Examen terminal
ECP31
Physique du mouvement II
Durée 1,5 heure
UFR Sciences

𝑟!
𝑇!=𝒢𝑚+𝑀 4𝜋!.!
Comment appelle-t-on la constante 𝒢 qui intervient dans cette relation ?
𝑎=!!
!
𝑁+!"
!"
𝑇=−𝑟𝜔!𝑢!+𝑟!"
!"
𝑢!. On en déduit, en projetant sur 𝑇 que 𝑣 est constante.
La projection sur 𝑁 donne la relation demandée.
𝒢 est la constante gravitationnelle, ou constante universelle de gravitation, ou constante de
Newton, ou constante de Cavendish.
6) Donner les caractéristiques des trajectoires 𝐸 et 𝑃 dans le référentiel barycentrique. Dessiner
qualitativement ces trajectoires et placer le centre de masse et les vecteurs vitesses des deux
corps. Quelles sont les périodes des mouvements de 𝐸 et 𝑃 ?
Cercles concentriques, centrés sur G. EG et P alignés. Même période T.
7) Appliquons maintenant ce qui précède au couple « Soleil – Terre ». On note 𝑀
! la masse du
Soleil qui est beaucoup plus élevée que celle de la Terre. En utilisant !𝑇=1 an et 𝑟=1 u.a.
(pour unité astronomique) dans la formule de la question 5), déduire la valeur de 𝒢!!
!!! dans ce
système d’unités particulier.
𝒢!!
!!!=1!u.a.3 an2.
Partie B : exoplanète
Une exoplanète est une planète gravitant autour d'une autre étoile que le Soleil. La première a été
découverte en 1995 dans la constellation de Pégase autour de l’étoile 51Pegasi.
La lumière émise par la planète étant complètement masquée par la luminosité de son étoile, il est
impossible de la voir directement. Pour détecter et caractériser une telle planète, on mesure en fait la
vitesse des petits déplacements de l’étoile dus à la présence de la planète : en observant le spectre
d'une étoile avec un spectromètre de très grande précision, on est capable de calculer, par effet
Doppler, les oscillations de la vitesse de l’étoile projetée sur la ligne de visée.
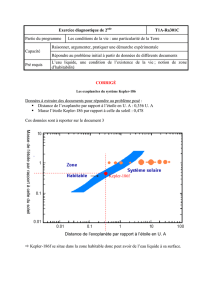
Dans le cas de la première exoplanète découverte,
cela a conduit au graphe ci-contre.
Ces observations laissent penser qu'il existe une
planète de masse m qui tourne autour de l'étoile de
masse M à la distance r. La période d'oscillation
correspond à la période orbitale de la planète. On
trouve ici 𝑇=4,233 jours.
En ce qui concerne l’étoile 51Pegasi, sa masse est
estimée à partir de sa luminosité et d’un modèle
stellaire. On obtient 𝑀=1,06!𝑀
!≫𝑚.
Dans cette partie B, nous allons appliquer les résultats de la partie A au couple « étoile –
planète ».
8) Calculer la période 𝑇 en années. En utilisant les questions 5) et 7), calculer alors la distance r
entre l’étoile 𝐸 et la planète 𝑃 en unité astronomique.
𝑇=!,!""
!"#,!"
=1,159×10!!!an. On en déduit que 𝑟=!!𝒢"
!!!!
!
!=0,0522!u.a..

9) Pour un mouvement circulaire uniforme, quelle est la relation entre la vitesse, le rayon de la
trajectoire et sa période ? La vitesse de rotation de l’étoile étant mesurée à 56!m.s!1, en
déduire la distance 𝐺𝐸 en mètres, puis en en unité astronomique. On donne 1!u.a.$ =
!149×10!!m.
𝑣=!!"
!. Appliqué à l’étoile, 𝐺𝐸 =𝑣!
!
!!
=3,395×10!!m=2,279×10!!!u.a.
10) En utilisant la question 3) dans le cas 𝑀≫𝑚, exprimer la masse de la planète en fonction de
la masse d’étoile. Faire l’application numérique en utilisant la masse solaire comme unité.
𝑚=𝑀!"
!
=4,63×10!!!𝑀
!.
II - Étude de la fusion entre noyaux lourds
Pour former un noyau lourd par collision nucléaire, on envoie un noyau projectile noté P ayant un
nombre de masse 𝐴! contre un noyau cible noté C et ayant un nombre de masse 𝐴!. Le noyau
composé obtenu par fusion est noté N et a un nombre de masse 𝐴!=𝐴!+𝐴!. Pour que la réaction
P+C→N puisse avoir lieu, une énergie –𝑄 doit être fournie au système (ici 𝑄<0). L’énergie
cinétique incidente, à savoir l’énergie cinétique du projectile, est notée 𝐸𝑐!. La masse du nucléon est
notée 𝑚!.
1) En notant 𝑣! la vitesse du projectile avant la collision, trouver 𝑣! la vitesse du noyau
composé.
𝐴!𝑚!𝑣!=𝐴!𝑚!𝑣!⇒𝑣!=!!
!!
𝑣!=!!
!!!!!
𝑣!
2) Quelle est l’énergie cinétique du noyau composé ? L’exprimer en fonction de l’énergie
cinétique incidente et en déduire l’énergie disponible pour la réaction.
𝐸𝑐!=!
!
𝐴!𝑚!𝑣!
!=!!
!!
𝐸𝑐!.
L’énergie disponible pour la réaction est donc : 𝐸𝑐!−𝐸𝑐!=!!
!!
𝐸𝑐!.
3) Quelle est l’énergie de seuil, à savoir l’énergie cinétique incidente minimale pour que la
réaction puisse avoir lieu ?
Il faut que !!
!!
𝐸𝑐!>−𝑄!⇒𝐸𝑐!>−!!
!!
𝑄.
4) Faire l’application numérique en MeV pour la réaction qui a permis de former le copernicium
pour la première fois en 1996 : Zn
70 +Pb 208 →Cn
112
278 . On donne 𝑄=!−244!MeV.
Il faut 𝐸𝑐!>326!MeV
III - Moment d’inertie d’un satellite
Afin de déterminer le moment d’inertie d’un satellite artificiel cylindrique par rapport à son axe de
révolution, on le suspend à un fil métallique et on le fait tourner dans un plan horizontal autour de sa
position d’équilibre. Le point d’attache est noté O. La rotation du satellite autour de son axe de
révolution est repérée par l’angle θ . Voir le dessin. Le point S est en A quand le satellite est à
l’équilibre.
Le fil exerce un couple de forces de rappel de moment 𝑀=−𝐶𝜃𝑢!, où θ est l’angle de rotation
du solide autour de l’axe vertical compté à partir de l’équilibre, C la constante de torsion et 𝑢! le
vecteur unitaire vertical vers le haut. On note I0 le moment d’inertie du satellite par rapport à l’axe de
rotation.
1) Définir le système étudié. satellite
2) Faire le bilan des forces et des moments appliqués au système. Poids, tension du fil et couple
de rappel.

3) Indiquer l’axe de rotation et le sens choisi.
4) A l’aide du théorème du moment cinétique, déterminer une équation différentielle satisfaite
par θ . En déduire la pulsation propre et la période T0 des oscillations.
!!!
!"
=𝑀!"# => !!!
!"
=𝑀 => 𝐼!𝜃=−𝐶𝜃. Et donc, 𝛺=!
!!
et 𝑇
!=!!
!
=2𝜋!!
!.
5) On ajoute deux masselottes identiques de masse m, situées symétriquement à la distance d de
l’axe vertical. Que vaut le nouveau moment d’inertie ?
𝐼=𝐼!+2𝑚𝑑!.
6) Montrer que la détermination expérimentale des périodes T0 et T, lorsqu’il y a les surcharges,
permet de connaître le moment d’inertie I0 du solide par rapport à son axe de révolution.
Comme précédemment, on a 𝑇=2𝜋!
!
=2𝜋!!!!!!!
!. Il y a deux inconnues : 𝐼! et 𝐶. A
l’aide des expressions de 𝑇 et 𝑇
! on déduit que 𝐼!=!!!!!
!
!
!!!!
!
!.