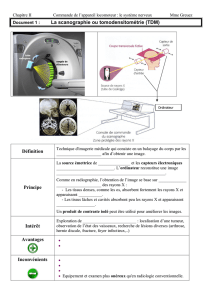
Arc-en-ciel - Étienne Thibierge

Correction de l’exercice à rendre le jeudi 5 novembre Langevin–Wallon, PTSI 2015-2016
Arc-en-ciel
Cet exercice représente 25 % du sujet de l’épreuve de physique A banque PT 2010, qualifié de « classique »
par le rapport du jury. À titre personnel je trouve qu’il est loin d’être simple, notamment car les difficultés
relèvent plus de la géométrie que de la physique. Néanmoins, ce genre d’exercice est posé de temps en
temps et il faut aussi s’y entraîner ...
Le présent corrigé ressemble largement à celui donné par Baptiste Percier à ses élèves de PCSI de
Besançon ... que certains d’entre vous ont clairement déjà trouvé tous seuls.
Barème : 18 points au total
A - Introduction
Les notations utilisées sont celles de la figure 1. L’angle iest l’angle d’incidence d’un rayon sur la bille sphérique,
compté par rapport à la normale à la bille. Comme la bille est sphérique, la normale passe par le centre de la bille.
L’angle rest l’angle de réfraction à l’intérieur de la bille, toujours compté par rapport à la normale. Les angles i
et rsont reliés de deux façons différentes : d’une part par la loi de la réfraction, d’autre part géométriquement pour
traduire le fait que le rayon réfléchi par la bille émerge parallèlement au rayon incident.
O
I
J
K
i
i
r
r0
r00
Fig. 1 –Rétro-réflecteur sphérique. Les trois angles r=r0=r00 sont égaux, comme démontré dans le texte.
La relation la plus simple à exprimer est celle issue de la loi de la réfraction, qui s’écrit
sin i=nsin r
en prenant l’indice de l’air égal à 1. Les rayons étant paraxiaux, on peut utiliser l’approximation des petits angles,
grâce à laquelle la condition s’écrit
i=n r .
Passons maintenant à la relation géométrique. Pour que cette deuxième condition puisse être vérifiée, il faut que
le point où le rayon réfléchi atteint le fond de la bille soit le point Jde la figure, tel que la droite (OJ)soit parallèle
au rayon incident. La symétrie par rapport à la droite (OJ)et le principe de retour inverse de la lumière garantissent
alors que le rayon sortant de la bille est parallèle à celui qui y entre. Comme le triangle (OIJ)est isocèle, on en déduit
l’égalité r0=r. Les angles r00 et r0étant alternes-internes, on en déduit également r00 =r0=r. Par conséquent,
l’égalité géométrique i=r+r00 devient
i= 2r .
Ce résultat peut en fait se montrer plus rapidement par le théorème dit de l’angle au centre.
En combinant les deux équations obtenues précédemment, on en déduit que l’indice du verre doit valoir 2
pour que la bille se comporte en rétro-réflecteur. C’est un indice très élevé, un réflecteur de ce type est donc
complexe à fabriquer.
Barème : 2.5 points
1/5 Étienne Thibierge, 16 novembre 2015, www.etienne-thibierge.fr

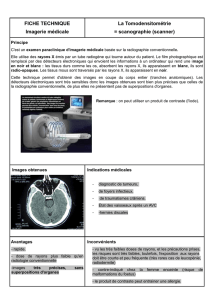
Correction DM pour le 5 novembre : Arc-en-ciel Langevin–Wallon, PTSI 2015-2016
B - Trajet des rayons dans une goutte d’eau sphérique
B.1.a On s’appuie à nouveau sur un schéma, figure 2, en identifiant dès que possible les angles iet r. Les propriétés
permettant ces identifications sont d’une part le caractère isocèle du triangle OIJ et la loi de la réflexion en Jet
d’autre part le principe de retour inverse en K.
Fig. 2 –Trajet des rayons dans une goutte sphérique. Cas d’une réflexion et de deux réfractions.
La déviation du rayon à chaque point d’incidence I,Jou Ks’obtient géométriquement :
au point I,i=r+DId’où DI=i−r;
au point J,r+r+DJ=πd’où DJ=π−2r;
au point K,i−DK=rd’où DK=i−r.
L’angle D1s’obtient ensuite par D1=π−DI J K , où DI J K =DK+DJ+DI, d’où
D1=π−(i−r)−(π−2r)−(i−r)soit D1= 4r−2i .
Barème : 2 points
B.1.b Les propriétés des angles externes permettent d’identifier i=[ IOH, d’où
sin i=HI
OI =h R=x .
On a donc i= arcsin x. D’après la loi de la réfraction au point I,sin i=nsin r, et donc r= arcsin(x/n). On en
déduit
D1= 4 arcsin x
n−2 arcsin x .
Barème : 1 point
B.1.c L’allure de la courbe est représentée figure 3. La fonction arcsin ne faisant pas (plus) partie des connaissances
exigibles, il est tout à fait légitime de tracer la courbe à la calculatrice ou avec Geogebra puis de reproduire son allure.
Fig. 3 –Angle de déviation D1en fonction de x=h/R.Tracé numérique pour n= 1,34.
2/5 Étienne Thibierge, 16 novembre 2015, www.etienne-thibierge.fr

Correction DM pour le 5 novembre : Arc-en-ciel Langevin–Wallon, PTSI 2015-2016
N’oubliez pas que les fonctions ont une signification en physique : les axes de la figure que vous construisez
doivent être légendés, gradués, et l’unité précisée lorsque nécessaire. Par ailleurs, les valeurs remarquables
(ici le maximum) doivent être indiquées.
Barème : 1 point, pénalités si la figure n’est pas correctement légendée.
B.1.d Trouver l’extremum demande de calculer la dérivée de la fonction D1.
dD1
dx=4 n
1
p1−(x/n)2−21 √1−x2
L’extremum x1m est obtenu lorsque la dérivée est nulle. Il est donc tel que
4
n
1
p1−(x1m/n)2−21 p1−x2
1m
= 0 soit n
4p1−(x1m/n)2=1 2q1−x2
1m
En élevant la dernière égalité au carré,
n2−x2
1m = 4 −4x2 1m
ce qui conduit enfin à
x1m =r4−n2
3.
Après un calcul de ce type, penser à vérifier la cohérence du résultat : x1m >0conformément au dessin
(on ne garde donc pas la racine avec le signe moins), et comme n < 2la racine carrée est bien définie.
Barème : 2 points
B.1.e Numériquement, pour une goutte d’eau,
x1m = 0,859 et D1m = 41,5°
ce qui est cohérent avec le tracé de la question précédente.
Penser à utiliser la calculatrice en degrés ! Rappelons aussi qu’une valeur numérique pour laquelle l’unité
est oubliée ne peut rapporter aucun point ...
Barème : 1 point
B.2.a On procède de la même façon qu’à la question B.1, en calculant les déviations successives. Il y a simplement ici
une réflexion supplémentaire au point L, voir figure 4, qui s’accompagne comme précédemment d’une déviation DL=
π−2r. On en déduit la déviation totale,
D2=DI J KL −π= (i−r)+(π−2r)+(π−2r)+(i−r)−πsoit D2=π+ 2i−6r .
Fig. 4 –Trajet des rayons dans une goutte sphérique. Cas de deux réflexions et de deux réfractions.
Barème : 1 point
B.2.b Numériquement,
D2m = 51,9°.
3/5 Étienne Thibierge, 16 novembre 2015, www.etienne-thibierge.fr

Correction DM pour le 5 novembre : Arc-en-ciel Langevin–Wallon, PTSI 2015-2016
Barème : 0.5 point
C - Caractéristiques de l’arc-en-ciel
C.1 La fonction D1(x)passant par un extremum en x1m, cela signifie que pour des valeurs de xpas trop éloignées
de x1m l’angle de déviation ne varie presque pas. Autrement dit, lorsque des rayons arrivent sur la goutte avec des
incidences variables, il y a davantage de rayons qui seront déviés dans une direction voisine de D1m : il y a donc un
regroupement de rayons, c’est-à-dire une accumulation de lumière, dans cette direction. Par conséquent,
les gouttes formant l’arc-en-ciel vu par l’observateur seront celles qu’il voit sous l’angle α1m défini sur la figure 5, où
βest l’inclinaison des rayons du soleil avec le sol.
Fig. 5 –Position relative du soleil, des gouttes et de l’observateur conduisant à l’observation d’un arc en ciel.
Barème : 2 points
C.2 L’arc secondaire s’explique de la même façon en considérant cette fois les rayons ayant subi deux réflexions
dans la goutte. Comme D2m 6=D1m, il y a formation d’un second arc, voir figure 6.
Fig. 6 –Arc primaire et arc secondaire.
Barème : 1 point
C.3 La « largeur angulaire » demandée par l’énoncé est commandée par la dispersion des rayons ... à laquelle
s’intéressent les questions suivantes. Je pense qu’ici l’énoncé veut plutôt parler rayon angulaire, qui correspond à α1m
pour le premier arc et α2m pour le second. La figure 5 permet de voir que α1m =D1m −β.
Par exemple, si le soleil se trouve à l’horizon (β'0), α1m = 41°et α2m =D2m −β'52°. Le point important
est qu’on a toujours α2m > α1m :l’arc secondaire est toujours externe.
Barème : 1 point
C.4 Le Soleil est « au zénith » lorsque ses rayons arrivent perpendiculairement au sol. Comme la latitude de Paris
est d’environ 45°, les rayons solaires forment un angle β= 45°avec le sol lorsque le Soleil est au zénith à l’équateur.
Dans ce cas, α1m <0: l’arc-en-ciel serait sous le sol, ce qui est impossible. Par conséquent, il n’est pas possible
de voir un arc-en-ciel à l’heure indiquée par l’énoncé.
Barème : 1 point
C.5 Les couleurs sont dues au fait que l’indice optique de l’eau dépend de la longueur d’onde : les « rayons
de différentes couleurs » sont déviés dans des directions légèrement différentes. À partir des valeur numériques
d’indices, on calcule que la déviation de l’arc primaire pour le violet D1V = 40,5670°est plus faible que pour le
rouge D1R = 42,4401°. Par conséquent, on remarque à partir de la figure 5 que le violet est vu sous un angle α1V plus
grand que le rouge α1R : comme tous les rayons du soleil ont à peu près la même inclinaison, la somme D1m +α1m
4/5 Étienne Thibierge, 16 novembre 2015, www.etienne-thibierge.fr

Correction DM pour le 5 novembre : Arc-en-ciel Langevin–Wallon, PTSI 2015-2016
est constante. Le rouge est donc à l’extérieur de l’arc primaire et le violet à l’intérieur. L’écart angulaire
entre les extrémités de l’arc externe vaut 1,8731°. Le même raisonnement permet de montrer que les couleurs sont
inversées pour l’arc secondaire, ce qui est visible sur la figure 7.
Fig. 7 –Photo d’un double arc-en-ciel. La rouge est à l’extérieur de l’arc primaire et le violet à l’intérieur. Les
couleurs sont inversées pour l’arc secondaire. Photo en couleur disponible sur le site de classe (et sur Wikipédia dont
elle est extraite).
Barème : 1 point
C.6 Tracer les courbes D1(x)et D2(x), figure ci-dessous, permet de voir qu’il existe un intervalle d’angles dans
lequel aucune lumière n’est réfléchie, alors que de part et d’autre de la lumière est réfléchie par les gouttes dans
la direction de l’observateur. Les limites de ce domaine sans réflexion sont les angles extrêmes de D1(x)et D2(x),
c’est-à-dire les angles sous lesquels sont vus les deux arcs. Par conséquent, la zone sombre se situe exactement entre
les deux arcs.
Barème : 1 point
5/5 Étienne Thibierge, 16 novembre 2015, www.etienne-thibierge.fr