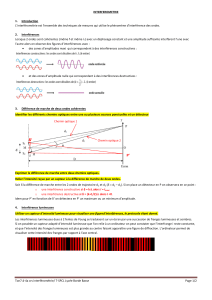
Interférences à deux ondes

IUT Saint Nazaire Département Mesures Physiques TP Optique Semestre 3
Ch2 Interférences à 2 ondes 1 © Bruno Velay
INTERFERENCES A 2 ONDES
1- Superpositions de deux ondes monochromatiques :
conditions d’interférence
L’amplitude totale résultant de la superposition de deux ondes planes progressives
monochromatiques de pulsation  et  est :
L’éclairement résultant en un point donné P est donné par :
 (où z* est le complexe conjugué de z)
!" #$% &
&'
&'
Q1a- Démontrer ce résultat préliminaire (rappel : cos b = (e
jb
+ e
-jb
) / 2 )
puis discuter des conditions d’interférences.
Discussion :
- Les ondes proviennent de deux sources différentes avec  ( (couleurs non
strictement identiques !)
#$% &
&'
&'
#$%)*
Deux sources de lumières de couleurs différentes n’interfèrent pas
→ +
,-
.
/-
0
12
.
2
0
simple addition des deux éclairements
- Les ondes proviennent de deux sources différentes avec 
3
!" #$%' &'
Mais si les deux ondes proviennent de deux trains d’ondes « incohérents » ' &'
varie aléatoirement et la moyenne est encore nulle.
Deux trains d’ondes incohérents n’interfèrent pas
→ +
,456789:;5<
12
.
2
0
- Les deux ondes proviennent de trains d’ondes « cohérents » (le plus souvent issus
du même train d’onde : voir plus loin les deux procédés possibles appelés
« division d’amplitude » et « division du front d’ondes »).
Deux trains d’ondes cohérents interfèrent
→ +
,6789:;5<
12
.
2
0
0"+
.
+
0
67,=>:
L’éclairement est alors modulé spatialement de façon spécifique selon
l’interféromètre utilisé.
→ possibilité d’exploitation en mesure.

IUT Saint Nazaire Département Mesures Physiques TP Optique Semestre 3
Ch2 Interférences à 2 ondes 2 © Bruno Velay
cohérence spatiale ?
2 trains d’ondes
« incohérents »
+
,456789:;5<
12
.
2
0
ou alors « cohérents » ?
+
,6789:;5<
12
.
2
0
0
"
+
.
+
0
67,
=
>
:
cohérence temporelle ?
A discuter selon l’interféromètre étudié
Stockage de données numériques dans un CD
Laser de lecture IR à 780 nm,
indice de réfraction du polycarbonate 1,55
Les informations numériques sont stockées dans un CD sous la forme d’un long
sillon formant une spirale dont le pas est 1,6 µm. Le sillon est gravé dans du
polycarbonate revêtue d’une couche métallique réfléchissante. Le sillon présente
des creux de profondeur 125 nm, de largeur 0,6 µm, de longueur variant entre 0,84
et 3,3 µm.
Q1b- Calculer la différence de « marche » (ou différence de « chemin optique »)
?@A entre deux ondes du faisceau de lecture lorsque le faisceau éclaire
perpendiculairement :
• pour moitié un creux, pour moitié un plat
• uniquement un creux ou un plat
En déduire dans ces deux cas, l’écart de phase =' entre les deux ondes envisagées.
En déduire le principe physique du codage mis en œuvre.

IUT Saint Nazaire Département Mesures Physiques TP Optique Semestre 3
Ch2 Interférences à 2 ondes 3 © Bruno Velay
2- Figures d’interférence pour deux sources ponctuelles
Par un procédé à définir selon l’interféromètre concerné, on dispose de deux sources
similaires ponctuelles, monochromatiques, synchrones et distantes de d :
B B B
C
D
ED
C
D
ED
avec F
G
H
On note 2
.
I
C
D
J
et 2
0
I
C
D
J
les éclairements en P dus à chaque source prise
séparément.
→ +
,6789:;5<
12
.
2
0
0"+
.
+
0
67,=>:
En pratique on a toujours BKB KB LM (typiquement 30 cm >> 1 mm)
On suppose donc que 2
.
K2
0
K2
N
KI
C
D
J
→ +
,6789:;5<
102
N
O.67,=>:P
Différence de phase au point P :
La différence de phase entre les deux ondes arrivant en P est :
=>:' &' FB &FB
G
H
B
&B
!Q
R
H
S
B &B
G
H
S
@B &B
0T
U
N
V où n est l’indice de réfraction du milieu optique et W
X
la
longueur d’onde dans le vide.
Différence de « marche » ou différence de « chemin optique » V@B &B
Attention : Y:Z@B est le « chemin optique » ≠ du simple trajet géométrique r.
+
,6789:;5<
102
N
[.67,\0T
U
N
V]^!
X
[_#$%\!Q
W
X
@B &B
]^

IUT Saint Nazaire Département Mesures Physiques TP Optique Semestre 3
Ch2 Interférences à 2 ondes 4 © Bruno Velay
Indicateur de l’état d’interférence entre les 2 ondes
Tout dépend de la comparaison des situations des 2 ondes et de leur décalage
exprimé comme une fraction de période
=>:
G
V
H
S
 il y a trois cas :
• Interférences « constructives » ? est multiple entier de W
X
où `ab a priori
donc
=>:
G
V
H
S
`
→ #$%='B`!Q_ → +
,cde
f02
N
g..hi
X
• Interférences « destructives » ? est multiple à un ½ entier près entier de W
X
où `abjklm
=>:
G
V
H
S
`*n
→ #$%`*n!Q&_ → +
,c45
f02
N
g.&.h*
• Interférences « intermédiaires » ? / W
X
est un réel quelconque
→ &_#$%I
V
H
S
!QJ_ → N+
,45<;:c9o4d4:;
fp2
N
Vue en coupe des surfaces sur lesquelles les interférences issues des sources
(indiquées par les flèches) sont constructives.
A droite, un zoom sur la partie centrale de la figure de gauche.

IUT Saint Nazaire Département Mesures Physiques TP Optique Semestre 3
Ch2 Interférences à 2 ondes 5 © Bruno Velay
3- Observation de franges d’interférence
Sur un écran placé dans un plan parallèle à l’axe Ox portant les deux sources, on
observe au voisinage du plan x = 0 des franges quasi rectilignes (tangentes à
l’origine des hyperboles de la figure précédente).
Représentation schématique des sources et de la position de l’écran d’observation
B qA \&M
!]
r Aq_\&Ms!
A]
Ir
AJ
B qA \M
!]
r Aq_\Ms!
A]
Ir
AJ
Un développement limité au 1
er
ordre suffira : t_uK_ ulorsque uv_
On constate ici que L >> x, y ou d donc x/L, y/L ou d/L <<1 Donc
q_\&Ms!
A]
Ir
AJ
K__
!w\&Ms! A]
Ir
AJ
x
K__
!wI AJ
\Ms!
A]
&Ms!
AIr AJ
x
On trouve B KA
y
z
&
{y
z
|
z
{
}z
et B KA
y
z
{y
z
|
z
{
}z
Le calcul au 1
er
ordre suffit puisque le résultat dépend de x. En effet :
Différence de « marche » V@B &B
V@B &B
K@!
{y
z
~V
5oe
•