FICHE METHODE ALGORITHMIQUE

FICHE METHODE
ALGORITHMIQUE
Le but de ces notes est de fournir quelques clefs pour aborder l'étude d'une situation où
l'algorithmique intervient. Cette fiche se complétera au fur et à mesure de l'année au cours de
laquelle les notions de boucle et de test (instruction conditionnelle) seront abordées.
La plupart des programmes seront écrits en « pseudo-langage » informatique, mais peuvent être
aisément traduits en tout langage : Python, Pascal, C++, langage de votre calculatrice, etc... Ce qui
compte, c'est le raisonnement sous-jacent, de la naissance de l'idée à la formalisation sur papier.
Vous devrez « faire tourner vos programmes » à la main pour vérifier s'ils sont corrects.
La notion de boucle
Cette notion fondamentale est extrêmement utile lorsqu'une même suite d'instructions doit être
répétée.
Nous avons vu en cours un type de boucle. Nous nous limiterons pour le moment à celui-ci.
Rappelons-le néanmoins :
Reprenons un exemple du cours en détaillant la démarche.
Problème : on veut calculer la somme
S=123…99100
.
Analyse : Bien évidemment, on ne va pas saisir à la machine cette longue opération ! Il nous faut
donc trouver un moyen pour que cette dernière l'exécute, mais en écrivant le moins de lignes.
On commence par remarquer que l'opération qui est sans cesse utilisée est l'addition. D'où l'idée
d'utiliser une boucle : on répète plusieurs fois le même procédé : ici additionner.
Additionner oui, mais quoi ? 1 d'abord, puis 2, puis 3, … , jusqu'à 100. Autrement dit on additionne
une suite de nombres qui « varient », dans le cas présent de 1 en 1.
L'idée essentielle est de calculer S petit à petit, comme on le ferait à la main en ajoutant peu à peu
tous les termes contenus dans l'addition.
Comme S va évoluer et les termes qui la composent aussi, on a l'idée d'introduire deux
variables : S elle-même et un « compteur » i, qui devra prendre successivement les valeurs 1, 2, 3,
…, 100.
Il nous faudra initialiser ces variables, c'est-à-dire leur donner une valeur de départ.
Mise en œuvre :
Instructions Signification
S ← 0
i ← 1
Tant que i ≤ 100 faire
S ← S + i
i ← i + 1
Afficher S
On affecte à S la valeur 0 (valeur initiale)
On affecte à i la valeur 1 (valeur initiale)
La condition est posée: i varie jusqu'à 100
On réaffecte à S sa valeur précédente + la valeur
de i
On réaffecte à i sa valeur augmentée de 1
Une fois sorti de la boucle, on affiche S
Tant que condition faire
Bloc d'instructions

Tant que la condition de la boucle (surlignée en rouge) est vérifiée, celle-ci s'exécute.
Faisons « tourner à la main » le programme pour les premiers termes.
Situation initiale
Comme i est égal à 1 et que
1100
, la condition de la boucle est bien vérifiée, donc cette
dernière exécute la suite d'instructions précédente :
•S est remplacé par sa valeur précédente : 0 à laquelle on rajoute la valeur actuelle de i : 1.
Ainsi, S = 0 + 1 soit S = 1.
•i est remplacé par sa valeur actuelle : 1 à laquelle on rajoute 1. Ainsi i = 1 + 1 soit i = 2.
Situation après une itération
Comme i est égal à 2 et que
2100
, la condition de la boucle est bien vérifiée, donc cette
dernière exécute la suite d'instructions précédente :
•S est remplacé par sa valeur précédente : 1 à laquelle on rajoute la valeur actuelle de i : 2.
Ainsi, S = 1 + 2
•i est remplacé par sa valeur actuelle : 2 à laquelle on rajoute 1. Ainsi i = 2 + 1 soit i = 3.
Situation après deux itérations
Et ainsi de suite... Tant que la condition de la boucle est valide, le bloc d'instruction est exécuté.
Situation après 99 itérations
Comme i est égal à 100 et que
100100
, la condition de la boucle est bien vérifiée, donc cette
dernière exécute la suite d'instructions précédente :
•S est remplacé par sa valeur précédente : 1+2+...+99 à laquelle on rajoute la valeur actuelle
de i : 100. Ainsi, S = 1 + 2 + … + 100
•i est remplacé par sa valeur actuelle : 100 à laquelle on rajoute 1. Ainsi i = 101
Situation après 100 itérations
Cette fois-ci, i est égal à 101, donc la condition de la boucle n'est plus valide. La boucle s'arrête. Le
programme effectue alors la dernière instruction (qui n'était pas dans la boucle) : afficher la valeur
de S, c'est-à-dire le résultat de 1 + 2 + … + 100.
i S
1 0
i S
2 1
i S
3 1+2
i S
100 1+2+...+99
i S
101 1+2+...+100

Je donne ci-dessous deux exemples de langages mettant en œuvre le programme précédent. Vous
remarquerez que chaque langage a sa propre syntaxe (très importante à respecter !).
Avec Algobox Avec le langage Python
1 VARIABLES
2 S EST_DU_TYPE NOMBRE
3 i EST_DU_TYPE NOMBRE
4 DEBUT_ALGORITHME
5 S PREND_LA_VALEUR 0
6 i PREND_LA_VALEUR 1
7 TANT_QUE (i<=100) FAIRE
8 DEBUT_TANT_QUE
9 S PREND_LA_VALEUR S+i
10 i PREND_LA_VALEUR i+1
11 FIN_TANT_QUE
12 AFFICHER S
13 FIN_ALGORITHME
# Ce programme calcule la somme des 100
premiers entiers naturels
S=0 # En Python, le symbole
i=1 d'affectation est le signe =
while i<=100: # while signifie « tant que »
S=S+i
i=i+1
print (S)
Les exercices suivants n'utilisent que la notion de boucle. Revenez sur la démarche précédente, il
n'y a que quelques modifications à apporter pour les résoudre. Ils sont corrigés à la fin de la fiche.
Exercice 1 : Écrivez dans chacun des cas un programme en pseudo-langage permettant de répondre
aux questions suivantes :
1. Calculer
S=369…201
2. Calculer
P=2×4×6×8×…×40
3. Calculer
T=11
21 2×31 2×3×4…1 2×3×4×…×10
Vous testerez ensuite vos algorithmes en les programmant sur le logiciel Algobox, en Python ou sur
votre calculatrice.
Exercice 2 :
1. Écrivez un programme qui donne les multiples de 9 en commençant à 90 et se terminant à
999.
2. Écrivez un programme qui donne les multiples de 9 en commençant à 90 et se terminant à
990 mais de 2 en deux ( 90 puis 108 et ainsi de suite )
Exercice 3 : Cet exercice nécessite l'utilisation du langage Python, notamment pour l'apport de son
outil « turtle », permettant de créer des figures géométriques grâce à des commandes simples. On en
rappelle quelques unes.
From turtle import *
reset()
goto(x,y)
forward(x)
backward(x)
up()
down()
left(x)
right(x)
Permet d'importer les commandes pour les
tracés.
On efface tout et on recommence
Aller à l'endroit(x,y)
Avancer de la distance x
Reculer de la distance x
Relever le crayon (pour pouvoir avancer sans
dessiner).
Abaisser le crayon pour recommencer à dessiner.
Tourner à gauche d'un angle en degrés égal à x.
Tourner à droite d'un angle en degrés égal à x.

1. Construire un carré de côté 60 en utilisant l'instruction while.
2. Construire la figure suivante en utilisant l'instruction while (longueur du côté du quadrillage
égale à 30). On partira du point central.
3. Construire la figure suivante en utilisant l'instruction while (longueur d'un côté du
quadrillage 50).On partira du point A.
4. En utilisant l'instruction while, soit une fois soit deux fois dans le même programme, obtenir
le dessin suivant :
Carré de côté 10 et intervalle entre les carrés 10.

Corrigé des exercices
Exercice 1
Question 1 : Il s'agit de sommer tous les multiples de 3 compris entre 3 et 201. L'idée est la même
que dans l'exemple phare : utiliser une boucle (car on répète l'opération « addition ») et utiliser deux
variables : i, variable qui va énumérer touts les termes à additionner et S (la somme recherchée qui
va évoluer à chaque itération de i). Un algorithme possible est :
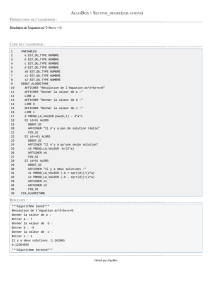
Avec Algobox Avec le langage Python
1 VARIABLES
2 S EST_DU_TYPE NOMBRE
3 i EST_DU_TYPE NOMBRE
4 DEBUT_ALGORITHME
5 S PREND_LA_VALEUR 0
6 i PREND_LA_VALEUR 3
7 TANT_QUE (i<=201) FAIRE
8 DEBUT_TANT_QUE
9 S PREND_LA_VALEUR S+i
10 i PREND_LA_VALEUR i+3
11 FIN_TANT_QUE
12 AFFICHER S
13 FIN_ALGORITHME
S=0
i=3
while i<=201: #Les « : » signifient « faire »
Le bloc d'instructions a une
S=S+i indentation par rapport à la
i=i+3 commande while
print (S)
Question 2 : Cette fois-ci, on multiplie tous les entiers pairs de 2 à 40.
On initialise le produit P à 1 (pourquoi pas à 0 ?)
On initialise i à 2
On remplace P par sa valeur précédente multipliée par la valeur
actuelle de i
i est incrémenté de 2 à chaque itération
S ← 0
i ← 3
Tant que i ≤ 201 faire
S ← S + i
i ← i + 3
Afficher S
P ← 1
i ← 2
Tant que i ≤ 40 faire
P ← P*i
i ← i + 2
Afficher P